Система завдань з теми «Чотирикутники» на уроках геометрії

Комунальний заклад «Нікопольська середня

загальноосвітня школа I-III ступенів № 25 з поглибленим

трудовим і профільним навчанням»

 

 

 

Система завдань з теми «Чотирикутники»

на уроках геометрії

 

 

 

                                                                                                   Підготувала:

учитель математики

Калєйнік Юлія Микoлаївна

 

 

 

 

 

 

 

                                                       2018 p.

Розв'язування задач при вивченні паралелограма

 

Задача 1. Периметр паралелограма дорівнює 122 см. Одна з його сторін більша, ніж друга, на 25 см. Знайти сторони паралелограма.

Розв'язання.

За теоремою [у паралелограмі протилежні сторони рівні, протилежні кути рівні і сума кутів, прилеглих до однієї сторони паралелограма, дорівнює 180°] протилежні сторони паралелограма рівні. Позначимо одну сторону паралелограма через х, другу - через у. За умовою

Розв'язуючи цю систему, одержимо x = 43, у = 18. Таким чином, сторони паралелограма дорівнюють 18, 43, 18 і 43 см.

Задача 2. Чотирикутник ABCD - паралелограм з периметром 10 см. Знайти діагональ BD, якщо периметр трикутника ABD дорівнює 8 см.

Розв'язання. Нехай умові задачі відповідає рис. 1. Позначимо AB через x, а ВС через у.

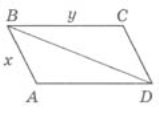
Рис. 1

За умовою периметр паралелограма дорівнює 10 см, тобто

2(х + у) = 10, або x + y = 5.

Периметр трикутника ABD дорівнює 8 см.

 

 

Оскільки:

АВ + AD = x + y = 5,

 то BD = 8 - 5 = 3.

Отже, BD = 3 см.

Задача 3. Знайти кути паралелограма, якщо відомо, що один із них більший від другого на 50°.

Розв'язання. Нехай умові задачі відповідає рисунок 2.

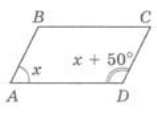
Рис. 2

Позначимо градусну міру кута А через х. Тоді градусна міра кута D дорівнює х + 50°.

Кути BAD і ADC внутрішні односторонні при паралельних прямих АВ і DC січній AD. Тоді сума цих кутів дорівнюватиме 180°, тобто

х + х + 50° = 180°, або х = 65°.

Таким чином,

∠A = ∠C = 65°, а ∠B = ∠D = 115°.

Задача 4. Сторони паралелограма дорівнюють 4,5 дм і 1,2 дм. 3 вершини гострого кута проведено бісектрису. На які частини вона ділить більшу сторону паралелограма?

Розв'язання. Нехай умові задачі відповідає рисунок Рис. 3.

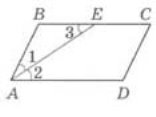
Рис. 3.

АЕ - бісектриса гострого кута паралелограма. Значить, ∠ 1 = ∠ 2.

ВС II AD, AE - січна, отже, ∠ 2 = ∠ 3, тобто ∠ 1 = ∠ 3. А це означає, що трикутник ABE рівнобедрений, значить, АВ = BЕ = = 1,2 дм.

ЕС = BС - BЕ = 3,3 дм.

Розв'язування задач при вивченні прямокутника

Задача 5. Пряма АВ паралельна прямій CD (рис. 4). Знайти відстань між цими прямими, якщо ∠ADC = 45°, CD = = 1,6 см.

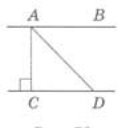
Рис. 4

Розв'язання.

Шукана відстань дорівнює довжині перпендикуляра АС. Трикутник ACD - прямокутний і рівнобедрений (АС - перпендикуляр, ∠ADC = 45° за умовою), отже, і ∠CAD = 45°, бо у прямокутному трикутнику сума гострих кутів дорівнює 90°. Значить, АС = CD = 1,6 см.

Задача 6. Знайти довжини діагоналей прямокутника ABCD (рис. 5), якщо периметр його дорівнює 34 дм, а периметр одного із трикутників, на які діагональ АС поділила прямокутник, дорівнює 30 см.

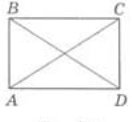
Рис. 5

Розв'язання. Позначимо периметр прямокутника ABCD через р, а периметр трикутника ABC - через p1. Трикутники ABC і ADC рівні (третя ознака рівності трикутників), значить, рівні і їх периметри.

Маємо:

2р1 - р = 2АС, або 60 - 34 = 2АС,

звідси AC = 13 см, значить (теорема 1), і діагональ BD дорівнює 13 см.

Задача 7. Бісектриса одного з кутів прямокутника ділить сторону прямокутника навпіл. Знайти периметр прямокутника, якщо його менша сторона дорівнює 10.

Розв'язання. Умові задачі відповідає рисунок 6.

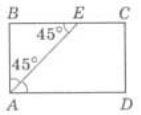
Рис. 6

BE = ЕС за умовою.

Трикутник ABE прямокутний і рівнобедрений. Значить, АВ = BE = 10.

ВС = 2 · BE = 2 · 10 = 20.

Периметр прямокутника ABCD дорівнює сумі усіх його сторін і дорівнює

2(АВ + ВС) = 2(10 + 20) = 60.

Розв'язування задач при вивченні ромба

Задача 8. Сторона ромба утворює з його діагоналями два кути, з яких один більший від другого на 50%. Обчислити кути ромба.

Розв'язання. Нехай умову задачі задовольняє рисунок 7.

 

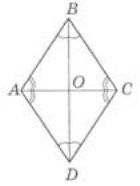
Рис. 7

 Позначимо градусну міру кута АВО через х, тоді ∠ВАО = x  + 0,5х = 1,5х.

За теоремою (діагоналі ромба взаємно перпендикулярні і ділять його кути навпіл), трикутник АОВ - прямокутний і, значить,

х + 1,5х = 90°,

 звідки x = 36°.

Згідно з тією ж теоремою маємо:

∠АВС = 36° · 2 = 72°,

 значить,

∠BAD = 180° - 72° = 108°.

Отже,

∠ADC = ∠ABC = 72° і ∠BСD = ∠BAD = 108°.

 

 

Розв'язування задач при вивченні трапеції

Задача 9. У рівнобічній трапеції перпендикуляр, проведений із вершини тупого кута, ділить більшу основу на відрізки 10 см і 20 см. Знайти меншу основу.

Розв'язання. Нехай умові задачі відповідає рисунок 8, а.

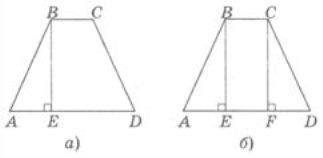
Рис.8

Проведемо другий перпендикуляр із вершини другого тупого кута

(рис. 8, б). Одержали два рівних прямокутних трикутники ABE і DCF. Із рівності цих трикутників випливає, що FD  = 10 см. Значить, EF = 20 - 10 = =10 см. Чотирикутник EBCF - прямокутник. Значить, ВС = EF = 10 см.

Задача 10. Середня лінія трапеції дорівнює 7 м, а одна з основ більша від другої на 4 м. Знайти основи трапеції.

Розв'язання. Позначимо довжину меншої основи через х. Тоді довжина більшої основи буде х + 4. Тепер, згідно з теоремою про середню лінію трапеції, одержимо рівняння:

розв'язуючи яке, знайдемо х = 5. Отже, основи трапеції 5 м і 9 м.

Задача11. Нехай вершини квадрата (розташовані за рухом годинникової стрілки), -його внутрішня точка, що знаходиться на однаковій відстані від та . Кут дорівнює . Обчисліть кут .

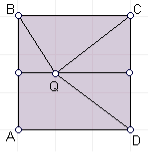Розв’язання. Нехай заданий квадрат, - задана точка, що лежить на серединному перпендикулярі відрізка , тоді , тобто трикутник - рівнобедрений. , отже, трикутник - рівносторонній. Враховуючи те, що , отримаємо: , тобто трикутник рівнобедрений. Оскільки , то .

Відповідь: Б) .

Прикладна спрямованість навчання геометрії найбільше реалізується при розв’язуванні прикладних задач. Під прикладними задачами в школі

здебільшого розуміють задачі, які виникають поза курсом математики і розв’язуються математичними методами і способами, які визначаються в шкільному курсі.

    У прикладних задача числові дані, як правило, мають бути наближеними, а при їх розв’язуванні необхідно використовувати обчислювальні засоби, зокрема ЕОМ.

    При розв’язанні прикладних задач у класах з поглибленим вивченням математики їх формулювання може бути розширене і являти собою деяке теоретичне зведення до проблеми, що вивчається.

   Знайомлячи учнів на уроках геометрії з абстрактними поняттями, необхідно показати їм конкретні об’єкти, співвіднести їх один з одним: плоска поверхня стола, класної дошки, дзеркала і крива поверхня м’яча, електричної лампи; туго натягнута нитка та нитка, що закріплена в двох точках і вільно висить та інше. Такі співвідношення допомагають установити причинно-наслідкові зв’язки явищ, що вивчаються.

      Основна частина задач прикладної спрямованості з даної теми пов’язана зі знаходженням площі та периметрів геометричних фігур.

 

 Наведемо приклади саме таких задач.

    Задача1.
      Скільки дошок потрібно, щоб настелити підлогу в кімнаті, довжиною 7.5 і шириною 5м, якщо довжина дошки 6м, а ширина 0.25м?

Розв’язання

 Поверхня підлоги має форму прямокутника, для знаходження площі, потрібно довжину помножити на ширину:

                                          S=7.5∙5=37.5(m2).
       Оскільки дошка теж має форму прямокутника, то її площа:   

                                          S2=6∙0.25=1.5(m2).

 Для того, щоб дізнатись, скільки потрібно дошок, треба:

                               k=S:S2 =37.5:1.5=25 (дошок).

Задача 2.

Будинок прямокутної форми розділений на 16 кімнат тієї ж форми, розміри яких невідомі. Відома площа 6 малих кімнат, які утворилися внаслідок розділення і їх площі навкдено на рис. 9. Знайдіть площі кожної з 4-х маленьких кімнат, розташованих у нижньому рядку якщо площа всього будинку 168.

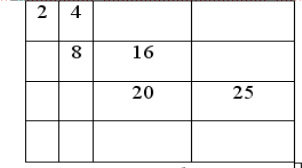
Рис. 9

Розглянемо мал.10, де через a, b, x, y позначено довжини выдповідних сторін, тоді S1=ax, S2= bx, S3=аy, S4=by, а тому маємо рівність: S1S4=S3S2. Таким чином, якщо ми знаємо площу трьох із чотирьох наведених прямокутників, то можна знайти і площу четвертого. Отже, на заданому в умові мал.1 можна обчислити площі всіх прямокутників, окрім тих, які розташовані у нижньому рядку. Зверху донизу їх площі такі: верхній ряд: 2, 4, 8, 10, другий ряд: 4, 8, 16, 20, третій ряд: 5, 10, 20, 25. Позначимо площу лівого нижнього прямокутника через х, тоді площі прямокутників нижнього ряду є: х, 2х, 4х, 5х. Таким чином площа великого прямокутника дорівнює 132 + 12х = 168, звідки х=3, і відповідні площі прямокутників нижнього рядка мають такі площі: 3, 6, 12, 15.

рис.10