Сценарій навчання вчителів природничо-математичної студії по впровадженню технології критичного та креативного мислення

Сценарій навчання вчителів природничо-математичної студії з упровадження технології критичного та креативного мислення

 

Тема: Креативна освіта як умова розвитку творчої особистості в процесі викладання предметів природничо-математичного циклу

 

          Мета: проаналізувати результати впровадження креативних методів навчання та виховання у навчально-виховний процес для розвитку компетентної, конкурентноздатної особистості, яка творчо вирішує реальні життєві проблеми, здатна до організації власних прийомів самонавчання та їх застосування для професійного та громадського практичного життя.

Передбачуваний результат: вироблення рекомендацій щодо підготовки креативного особистісно орієнтованого уроку.

 

                                                Хід заняття:

І частина. Презентаційний меседж « А я роблю так…»

1. Вправа «Три слова про себе».

 Кожний вчитель, використовуючи всього три слова характеризує сутність терміну «креативний вчитель».

Мета: виділити основні аспекти креативності, що характеризуються створенням суб’єктивно нового продукту, загальні вимоги до процесу креативного мислення незалежно від проблеми, на яку він спрямований.

2. Анкетування. Тест «Вивчення творчого потенціалу вчителя» (А.Н.Лук) в порівнянні  з  результатами  попередніх  анкетувань.

Мета: виявити рівень творчого потенціалу і проаналізувати зміни в творчому потенціалі вчителів, які відбулися за час роботи по реалізації науково-методичної проблеми природничо-математичної студії «Використання технології партнерства для розвитку креативності суб’єктів освітнього середовища».

         3. Вправа «Асоціативний ряд»

Мета: активізувати мислення вчителів шляхом висловлювання власних думок, для розкриття сутності поняття  «креативність».

 

К	компетентність, кмітливість, комунікабельність
Р	результативність, реагування, рефлексія
Е	емоційність, ерудиція, емпатія
А	актуальність, активність
Т(и)	талант, тьютор, тренінг
В	вимогливість, винахідництво, взаємодія
Н	науковість, наполегливість, новація
І	інтелект, інтроверсія, інтуїція
С	самоактуалізація, самоосвіта, самоконтроль
ТЬ	творчість, толерантність

 

4.Презентація досвіду роботи вчителів природничо-математичної студії (Додаток 1)

1. Розвиток креативного мислення учасників навчально-виховного процесу в процесі викладання математики ( Гавриш С.П.)

2. Формування креативного мислення учнів під час пізнавальної діяльності на уроках фізики (Яресько І.П.)

3.Технологія розвитку креативного мислення на уроках хімії (Глазунов М.М.)

4. Креативне навчання на уроках географії (Пазяк І.Б.)

5. Впровадження хмарно-орієнтованої моделі навчання засобами хмарного середовища Office 365 (Буланова І.М.) https://www.youtube.com/watch?v=FJw-A8D96QE&feature=youtu.be 

 

ІІ частина. Естафета вчительських здивувань (Додаток 2)

Мета: обмін досвідом по проведенню уроків з використанням технології креативного навчання та виховання, розкриття творчого потенціалу кожного педагога, розробка рекомендацій з підготовки креативного особистісно орієнтованого уроку .

1. Урок географії на тему «Південна Америка – найвологіший материк. Практична робота №5. Позначення на контурній карті географічних об’єктів материка» (вчитель Пазяк І.Б.).

2. Проведення веб-квесту «Будова ПК» засобами  хмарного середовища Office 365 (вчитель Буланова І.М.)

3. Урок  хімії «Оксиген у природі. Озон. Проблема чистого повітря»

(вчитель Глазунов М.М.)

4. «Вправи і творчі завдання на уроках математики для розвитку креативних здібностей учнів» (вчитель Гавриш С.П.)

 

            Рекомендації з підготовки креативного особистісно орієнтованого уроку:

 

1. Під час проведення уроків дотримуватися оптимального співвідношення всіх дидактичних принципів і правил, раціонально поєднувати різні форми і методи навчання.
2. Забезпечити творчий підхід до формування структури уроку, обдумувати можливості для самопрояву учнів.
3. В ході уроку проводити процедуру відслідковування (спостереження за учнями), заохочувати їх до висловлювання оригінальних ідей, гіпотез.
4. Стимулювати учнів до активних дій із залученням знань, суб’єктивного досвіду, рецензуванню відповідей.
5. Створювати ситуації успіху для кожного учня протягом всього уроку.

            При підготовці до уроку використовувати альтернативні шляхи пошуку інформації, використовувати Інтернет ресурс, хмарне середовище      Office 365.

6. Стимулювати учнів до роботи в сучасному інформаційному просторі.
7. З метою розвитку креативності, творчої ініціативи й активності учнів на позакласних заходах домагатися формування цілісного сприйняття фактів, подій і процесів у природі та сучасному житті.

 

 

 

Додаток 1

1. Розвиток креативного мислення учасників навчально-виховного процесу в процесі викладання математики (доповідач С.П.Гавриш)

 

Наш час – це час суттєвих змін у науці, техніці, інформаційному середовищі, освіті. Суспільству потрібні люди, які здатні приймати нестандартні рішення, вміють творчо мислити. Як зазначено у Національній доктрині розвитку освіти, «Держава повинна забезпечувати розвиток творчих здібностей і навичок самостійного наукового пізнання, самоосвіти і самореалізації особистості». Одним із вирішальних чинників розв’язання цих завдань є розвиток креативного мислення учнів. Що ж таке креативність?

 

 

 

 

 

               Творчий                                                    Створення

За схемою бачимо, що термін «креативність» має подвійне значення: творчість і створення. Але треба пам’ятати, що творчість не завжди дає творчий результат, а креативність веде до створення творчого продукту.  

 

Креативне навчання – це процес постійної співпраці вчителя та учня. Навчальний процес організовується як живий контакт партнерів, зацікавлених один у одному та в справі, якою вони займаються разом. Креативне навчання має характерну рису: навчальний процес зливається з життям, із рішенням реальних творчих задач.

Важливо, щоб учні розуміли, що творчість починається саме із сумніву. Дуже дієвим на уроках є створення проблемних ситуацій, формулювання проблемних питань, висування проблемно-пошукових гіпотез. Наприклад, під час вивчення теми «Сума кутів трикутника», щоб краще привернути увагу учнів до теореми, корисно провести деяку попередню роботу:

- Спробуйте побудувати трикутник, у якого кожен кут дорівнює 80°...

- Один кут трикутника дорівнює 50°, другий - 100°. Чи зможете ви знайти градусну міру третього кута?...

- Накресліть кожен у своєму зошиті якийсь трикутник. А тепер виміряйте всі три його кути і знайдіть їхню суму...

У всіх трьох наведених випадках перед формулюванням теореми створюється проблемна ситуація: ставляться запи­тання, на які учні поки що не можуть дати обґрунтованої відпові­ді. Звичайно, постановка таких питань привертає увагу учнів. Вони чекають на відповідь і тому - максимально уважні.

Розгляд софізмів розвиває спостережливість, вдумливе і критичне ставлення до того, шо вивчається, виховує в учнів критичне мислення.

Математичні софізми привчають ретельно стежити за точністю формулювань, правильністю записів і креслень при розв’язуванні задач. За допустимістю узагальнень. До того ж розгляд софізмів захоплюючий.

Так наприклад в 6 класі при вивченні теми «Ділення раціональних чисел» для зацікавлення учнів і розвитку в них логічного мислення  використовую такий софізм:

Стверджую, що 5=6. Для доведення цього використовується числова рівність: 35+10-45=42+12-54. Отримаємо:5(7+2-9)=6(7+2-9). Поділимо обидві частини на спільний множник. Отримаємо5=6. Де помилка?

Учні, які засвоїли, що на нуль ділити не можна дають відповідь на задане  запитання.

При вивчені у 8 класі теми «Властивості арифметичного квадратного кореня» розглядаю такий софізм: Стверджую, що 2=3. Маємо: 4-10=9-15,  4-10+= 9 - 15+,  (2- =(3-,  2 - =3 -. Отже 2=3. Де помилка?

Щоб  розв’язати  задачу,  потрібно  умову  задачі  перевести  на  мову  алгебри.  Мова  алгебри – рівняння.  «Щоб  вирішити  питання,  яке  відноситься  до  чисел  або  до  відношень  величин,  потрібно  перекласти  задачу  з  рідної  мови  на  мову  алгебри», – писав    великий  Ньютон  в  своєму  підручнику  «Загальна  арифметика».  Як  зробити  переклад  з  рідної  мови  на  мову  алгебри,  Ньютон  показав  на  прикладах.  Ось  один  із  них:

На  рідній  мові:	На  мові  алгебри:
Купець  мав  деяку  суму  грошей.
За  перший  рік  він  витратив  100  фунтів.
До  грошей,  що  залишились,  добавив  їх  третю  частину
За  наступний  рік  він  знову  витратив  100  фунтів
І  збільшив  решту  грошей  на  її  третю    частину.
За  третій  рік  він  знову  витратив  100  фунтів.
Після  того  як  він  добавив  до  решти  її  третю  частину,
грошей  в  нього  стало  в  двічі  більше.

Щоб  знайти  скільки  грошей  було  в  купця  спочатку,  потрібно  лише  розв’язати   останнє  рівняння.

         Вправа «Не помились». На дошці записані такі числа: 6, 9, 8,3, 7, 5, 2, 4. Учні, які сидять один за одним, повинні швидко дати відповідь від множення кожного із цих чисел, наприклад на 8.

Саме впровадження на уроці креативних, розвиваючих ігор може сприяти розвитку пізнавальної активності в школярів. Використання нетрадиційних уроків-ігор дає змогу практично застосовувати математичні знання дітей. Для цього вчителям необхідно володіти сучасними методами, які б пробуджували у школярів бажання пізнавати нове, незвідане. Хорошим доробком у цій справі будуть розвиваючі вправи та завдання. Набір дидактичних розвиваючих ігор, вправ, може сприяти розвитку різноманітних якостей і здібностей у дітей, для допомоги у тому, щоб проявляти і реалізовувати пізнавальну активність у процесі розкриття і засвоєння шкільного матеріалу. 

Так, у своїй роботі на уроках математики я використовую систему запитань, створюючи різного роду ігрові ситуації або вносячи творчі елементи, завдяки чому учні отримають змогу активізувати розумову діяльність, робити висновки. Серед основних типів завдань такі:

1. Завдання з незформульованими запитаннями.

Приклад. Шоколад коштує 15 грн, коробка цукерок 30 грн. Вкажіть всі можливі питання за умовою завдання.

2. Завдання з відсутніми даними.

Приклад. З двох пунктів виїхали одночасно два автомобіля. Швидкість одного з них дорівнює 65 км/год, а швидкість іншого - на 7 км/год більша. Яка відстань буде між автомобілями через 2 години?

Учням ставлю запитання: Чому не можна дати відповідь на запитання задачі?

Чого не вистачає?  Що потрібно додати? Доведи, що тепер завдання точно можна буде вирішити? А можна що-небудь отримати навіть з наявних даних? Який висновок можна зробити з аналізу того, що дано?

3. Задачі із зайвими даними.

У 21 кг рису містится16 кг крохмалю а у 12 кг ячменю – 7 кг крохмалю.  У магазин привезли 42 кг рису та 14 кг ячменю. Де крохмалю більше – в 1 кг рису чи і 1 кг ячменю?

4. Завдання з кількома розв’язками.

Приклад. За три дні в магазині продано 1280 кг яблук. У перший день продали 25% всіх яблук, а у другий день - 45% усіх яблук. Скільки кілограмів яблук продали в третій день? Розв'яжіть задачу кількома способами. Який з них найбільш простий.

5. Завдання зі зміною умови.

Приклад. Вихідна задача. Туристи пройшли за день 20 км, що склало 40% наміченого маршруту. Яка довжина маршруту?

Другий варіант. Туристи пройшли за день 20 км і їм залишилося пройти 60% наміченого маршруту. Яка довжина маршруту?

6. Завдання на доведення.  Саме при виконанні доведень відточується логічне мислення учнів,  розробляються логічні схеми розв’язування задач, виникає потреба в обгрунтуванні  математичних фактів.

Приклад. Доведіть, що сума будь-яких двох послідовних непарних чисел ділиться на 4.

7. Завдання на логічне міркування, дослідження.

Для прикладу в 6 класі я задаю наступні задачі:

• Чи існують числа обернені самі собі. Скільки таких чисел ? Назвіть їх.   При яких значеннях а і в правильні:
• а) Рівності а/b=0;a/b=1;a/b=-1.
• б) Нерівності ab>1; a/b>1; a/b<-1.

        Найважливішими математичними операціями є аналіз і синтез.  Аналіз пов'язаний з виділенням елементів даного об'єкта, його ознак або властивостей. Синтез – поєднання різних елементів, сторін об'єкта в єдине ціле. У розумової діяльності аналіз і синтез доповнюють один одного. Формуванню та розвитку даних розумових операцій сприяє рішення задач, у яких від учнів вимагається проводити правильні міркування, розглядати об'єкти з різних сторін, вказувати їх різні властивості, а також постановка різних питань щодо даного об'єкта.    Ось деякі завдання:

1.Як розрізати фігуру на три рівні частини?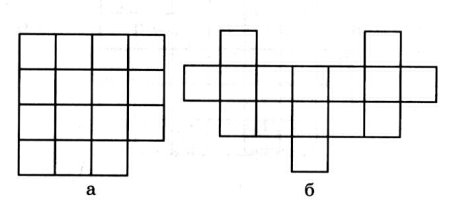

Відповідь:

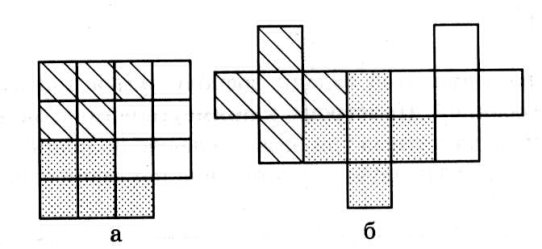
2. Скільки трикутників на малюнку?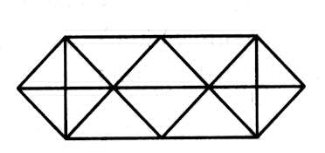                                          

      Відповідь: Всього 28 трикутників.

 

2. Який знак потрібно поставити між 2 і 3, щоб вийшло число більше за 2, але менше 3? (Відповідь: кому. 2,3.)

 

4. До царя Гороха дійшла чутка, що хтось з трьох богатирів убив Змія Горинича. Цар наказав усім трьом з'явитися до двору, і мовили вони:              Ілля Муромець: «Змія вбив Добриня Микитич».

Добриня Микитич: «Змія вбив Альоша Попович».

Альоша Попович: «Я вбив змія».

При цьому виявилося, що один з них сказав правду, а двоє злукавили. Хто вбив змія? (Відповідь: Змія вбив Добриня Микитич.)

 

5. Ліза, Галя і Ніна жили в різних будинках. Будинок № 1 – високий кам'яний, № 2 – високий дерев'яний, № 3 – невисокий кам'яний. В якому будинку жила кожна з дівчаток, якщо Галя і Ніна жили у високих, а Ніна і Ліза – в кам'яних? (Відповідь: Ніна жила в будинку № 1, Галя жила в будинку № 2, Ліза жила в будинку № 3. )