Серія уроків алгебри по темі "Показникова функція"
Дані матеріали містять розробки уроків з алгебри по темі «Показникова функція» для класів загальноосвітніх навчальних закладів, навчання яких відбувається за рівнем «стандарт».
Урок № 1
Тема. Показникова функція
Мета: сформувати поняття степеня з дійсним показником; знання про означення, вид графіка показникової функції; вміння виконувати побудову графіка функції у = ах, визначати іі властивості за графіком; розвивати креслярські навички; виховувати в учнів графічну культуру.
Тип уроку: формування нових знань і первинних умінь.
Обладнання: мультимедійний проектор, екран, опорні конспекти для учнів.
Програмне забезпечення: ППЗ «Алгебра 10 клас»
Хід уроку
І. Організаційний етап
Перевірка учителем готовності учнів до уроку.
ІІ. Підготовка учнів до активного свідомого засвоєння знань
2.1. Звіт помічників про наявність д/з у учнів.
2.2. Вправа «Кошик знань». Вчитель називає перше слово, а учні «ланцюжком» доповнюють «кошик» основними термінами, поняттями. Наприклад: функція – графік – область визначення функції …
2.3. Питання на повторення
Методичний прийом «Продовжити речення»
1. Функцією називають …
2. Незалежну змінну х називають…
3. Залежну змінну у називають…
4. Графіком функції називають…
5. Областю визначення функції називають…
 6. Областю значень функції є…
6. Областю значень функції є…
7. Точки перетину з віссю Ох називаються …
2.4. Усні вправи
1. Використовуючи графік даної функції, назвати:
1) D (f);
2) E (f);
3) нулі функції;
4) проміжки зростання та спадання функції;
5) проміжки знакосталості функції.
2. Назвіть дану функцію.
3. Дати означення степеня з раціональним показником.
4. Обчисли: ![]()
![]() (2,25)0;
(2,25)0; ![]() ;
; ![]() ;
; ![]() .
.
5. Пригадати основні властивості степенів, використовуючи таблицю.
Властивості степеня з раціональним показником
|
am∙an = am + n |
|
|
am׃an = am – n |
|
|
(am)n = am∙n |
|
|
(ab)n = an∙bn |
|
|
|
|
6. Подати у вигляді степеня або добутку степенів вираз:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4)  ; 5)
; 5) ![]() .
.
ІІІ. Формулювання теми, мети, завдань уроку
На даному етапі уроку слід зазначити, що поняття степеня з раціональним показником можна розширити до степеня з ірраціональним показником та будь-які дійсні показники степенів, зберігаючи при цьому властивості степенів, вміщених у таблицю (див. вище). Крім цього наголосити, що в природі існує багато процесів, які описуються різними функціями. Сьогодні на уроці розглянемо одну з таких функцій.
ІV. Формування знань
4.1. Степінь з ірраціональним показником.
Розглянемо степінь ![]() з ірраціональним показником.
з ірраціональним показником.
![]()
Нехай а1 та а2 відповідно наближені значення цього десяткового дробу з нестачею та надлишком. Причому а1 та а2 є раціональними числами. Тоді ![]() , а за властивостями степенів
, а за властивостями степенів ![]() .
.
Візьмемо а1 = 1, 732050 і а2 = 1,732051. Обчислимо відповідні значення степенів ![]() = 3, 3219952 та
= 3, 3219952 та ![]() = 3,32119975. Різниця значень – надзвичайно мале число. Тому можна розглядати наближені значення степеня
= 3,32119975. Різниця значень – надзвичайно мале число. Тому можна розглядати наближені значення степеня ![]() з будь-якою точністю з нестачею і надлишком.
з будь-якою точністю з нестачею і надлишком.
4.2. Означення показникової функції.
Даємо формальне означення показникової функції: «Функцію, яку можна задати за допомогою формули у = ах, де а![]() 0 – фіксоване число (параметр), а 1, називають показниковою».
0 – фіксоване число (параметр), а 1, називають показниковою».
Наприклад: у = 2х; у = 3х; ![]() .
.
Зауважуємо, що показникові функція задається степенем, у якого показником є незалежна змінна.
4.3. Графік показникової функції.
Пропонуємо розглянути графік функції у = 2х та встановити властивості функції за графіком. Для ілюстрації графіка функції можна використати ППЗ «Алгебра 10 клас» або опорний конспект уроку. Як варіант можна побудувати графік функції у = 2х за допомогою точок, склавши відповідну таблицю значень аргументу та значень функції.
4.4. Властивості показникової функції.
Використовуючи графік функції у = 2х , назвати:
1) D (f);
2) E (f);
3) нулі функції;
4) проміжки зростання та спадання функції;
5) проміжки знакосталості функції.
Звіряємо описані властивості з опорним конспектом, робимо висновки.
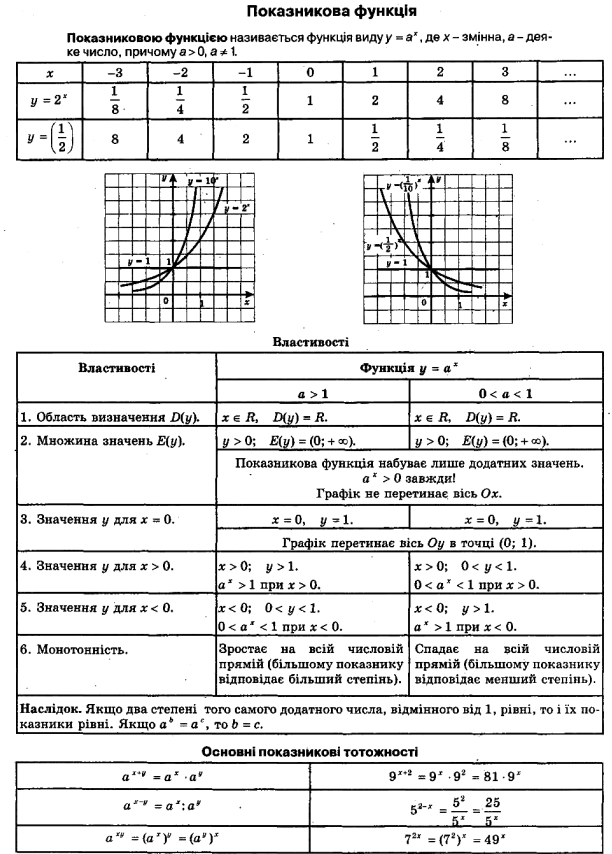
Завдання 1. Побудувати графік функції ![]() , використовуючи опорний конспект та перевірити властивості даної функції.
, використовуючи опорний конспект та перевірити властивості даної функції.
Завдання 2. Порівняти графіки функцій у = 2х та ![]() , визначити спільні характеристики.
, визначити спільні характеристики.
Завдання 3. Використовуючи опорний конспект, самостійно ознайомитись з основними показниковими тотожностями.
Висновок: всі властивості степенів з дійсними показниками справджуються для показникової функції.
4.5. Фізкультхвилинка.
V. Формування вмінь
5.1. Усні вправи
1. Укажіть, яка з даних функцій зростаюча, яка – спадна на множині R:
а) ![]()
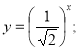 б)
б) ![]()
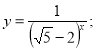
в) ![]()
![]() ; г)
; г) ![]()
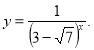
2. Знайдіть область визначення функції:
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]() д)
д) ![]()
3. Знайдіть множину значень функції:
а) ![]() б) у = 1х; в) у = 3х – 1.
б) у = 1х; в) у = 3х – 1.
5.2. Письмове виконання вправ
1. Знайдіть множину значень функції:
а) ![]() б)
б) ![]() ; в)
; в) ![]()
5. Знайдіть найбільше і найменше значення функції:
а) ![]() ; б)
; б)![]() .
.
Додаткові завдання
6. Знайдіть знак кореня рівняння:
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
7. Розв’яжіть графічно рівняння:
а) ![]() б)
б) ![]() .
.
VI. Підсумки уроку
6.1. Питання на повторення.
6.2. Оцінювання результатів навчальної діяльності учнів.
6.3. Оголошення д/з. Обов’язковий рівень:
1. Побудуйте графіки функцій
а) у = 3х та ![]() ;
;
б) у = -2х та у = -2-х;
в) у = 1х.
2. Знайдіть найбільше і найменше значення функції:
а) ![]() б)
б) ![]()
3. Розв’яжіть графічно рівняння:
а) ![]() б)
б) ![]()
Підвищений та творчий рівень
4. Задано функцію 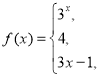
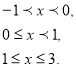
Побудуйте її графік. Знайдіть f(2), f(0), f ![]() , f
, f ![]() , f(3).
, f(3).
5. Побудувати графік функції ![]() .
.
Розв’язання
Функція визначена для довільних значень аргументу х. Графік функції симетричний відносно осі ординат. Найбільше значення функції є 1 при х = 0. При х = ![]() функція має значення 0,5, а при х =
функція має значення 0,5, а при х = ![]() 2, у =
2, у = ![]() .
.
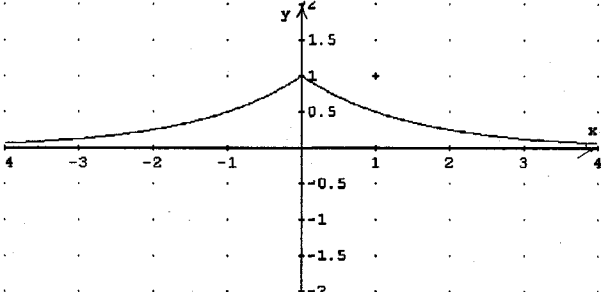
Додаткові завдання
1. Побудувати графік функції |y| = 2x – 1.
Область визначення функції знаходимо із нерівності ![]() , звідки
, звідки ![]() . Отже, функція визначена на проміжку [0:+ ∞). Будуємо графік функції у = 2х-1 (для
. Отже, функція визначена на проміжку [0:+ ∞). Будуємо графік функції у = 2х-1 (для ![]() ) на проміжку [0:+ ∞) і відображаємо його відносно осі абсцис.
) на проміжку [0:+ ∞) і відображаємо його відносно осі абсцис.
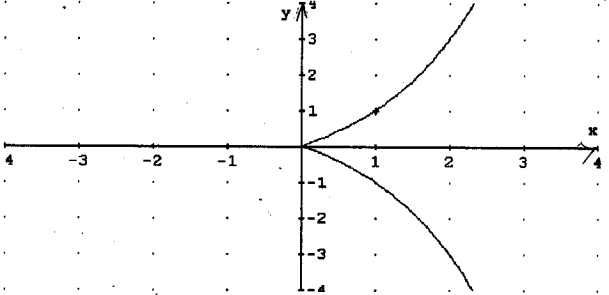
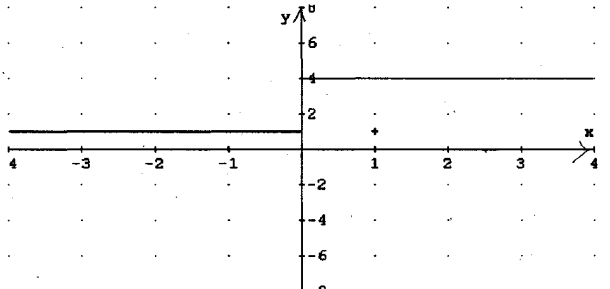
2.Побудувати графік функції y = 2(|x| + x)/ x
Областю визначення функції є вся числова пряма, крім нуля. Рівняння розпадається на 2:
![]()
Завдання для творчих груп
Учні класу об’єднуються у 4 творчі групи за власним вибором. Групам оголошуються такі завдання:
І група – дослідники – науковці. Готує матеріал про існування функції певного виду за допомогою якої можна описати більшість природних явищ.
ІІ група – фізики – теоретики. Досліджує використання показникової функції для опису явищ навколишнього середовища.
ІІІ група – біологи. Розкривають тему «Розмноження живих організмів».
ІV група – історики. Добирає матеріал про історію досліджень властивостей показникової функції.
Урок № 2
Тема. Використання показникової функції під час вивчення явищ навколишнього середовища
Мета: показати учням практичне використання показникової функції та її властивостей при вивченні явищ навколишнього середовища; розвивати пізнавальний інтерес учнів до вивчення предмету, дослідницькі навички; виховувати відповідальне ставлення до результатів власної інтелектуальної праці.
Тип уроку: формування нових знань і первинних умінь.
Обладнання: ПК, проектор, екран, тематичні презентації учнів, опорні конспекти, роздатковий матеріал.
Хід уроку
І. Організаційний етап
Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.
ІІ. Перевірка домашнього завдання
Збираємо зошити на перевірку.
ІІІ. Формулювання мети і завдань уроку
Мотивація навчальної діяльності учнів
Великий Галілео Галілей казав, що природа формулює свої закони мовою математики. Сьогодні на уроці розглянемо зв'язок показникової функції з природними явищами. А спочатку розглянемо задачу про незчисленний улов. Отже, 3 рибалки, втомившись після успішної риболовлі, заснули. Перший рибалка, прокинувшись, поділив весь улов на 3 частини. Тоді одну частину улову випустив назад у море і поїхав додому. Другий рибалка, прокинувшись пізніше, знову поділив всю рибу на 3 частини, одну частину випустив у море і теж поїхав додому… Скільки риби піймали рибалки?
IV. Формування знань
Звіт творчих груп
І група – дослідники – науковці. Звітує про існування функції певного виду за допомогою якої можна описати більшість природних явищ.
Короткий зміст
У практичному застосуванні показникові функції зустрічаються здебільшого у вигляді ![]() . Покажемо, що функцію виду
. Покажемо, що функцію виду ![]() можна перетворити до виду
можна перетворити до виду ![]() . Розглянемо функцію
. Розглянемо функцію ![]() . Графік даної функції перетинає вісь ординат у точці (0; С). Далі дослідимо при яких значеннях С графік функції
. Графік даної функції перетинає вісь ординат у точці (0; С). Далі дослідимо при яких значеннях С графік функції ![]() розміститься над віссю абсцис (під віссю). Доповідь ілюструємо графіками функцій.
розміститься над віссю абсцис (під віссю). Доповідь ілюструємо графіками функцій.
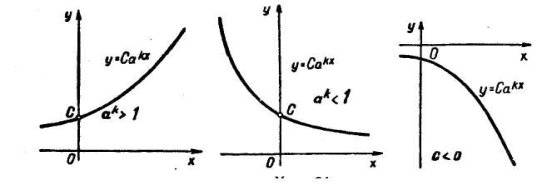
Аналізуючи графіки, робимо висновок: при С ![]() графік функції
графік функції ![]() розміщений вище осі абсцис (мал. 1; 2), при С
розміщений вище осі абсцис (мал. 1; 2), при С ![]() - нижче осі абсцис (мал. 3). Всі графіки проходять через точку (0; С).
- нижче осі абсцис (мал. 3). Всі графіки проходять через точку (0; С).
ІІ група – фізики – теоретики.
Короткий зміст
Показникова функція широко застосовується в науці і техніці. Наприклад, процес радіоактивного розпаду ядер таких хімічних елементів як радій, уран, радон тощо. Розглянемо докладніше.
Задача про радіоактивний розпад.
Позначимо через Т проміжок часу, за який маса радіоактивної речовини зменшиться вдвічі (Т – період напіврозпаду речовини). Для різних радіоактивних речовин період напіврозпаду різний. Для урану Т = 4,56 млрд. років, для радію Т = 1590 років. Якщо через х виразити відношення будь якого проміжку часу t до періоду напіврозпаду Т (х = ![]() ), то х є мірою розпаду речовини. Позначимо через у відношення маси (m) речовини, що залишилася за цей проміжок часу, до початкової маси речовини М, тобто
), то х є мірою розпаду речовини. Позначимо через у відношення маси (m) речовини, що залишилася за цей проміжок часу, до початкової маси речовини М, тобто ![]() . Таким чином у – частина речовини, що залишилася через t років. Тому процес розпаду ядер радіоактивних речовин можна виразити формулою
. Таким чином у – частина речовини, що залишилася через t років. Тому процес розпаду ядер радіоактивних речовин можна виразити формулою
![]() або
або 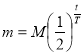 .
.
Коли в цій формулі х змінюється в арифметичній прогресії (х = 1, 2, 3, …), то у зменшується в геометричній прогресії (у = ![]() ,
, ![]() ,
, ![]() , …).
, …).
Більш загальною формулою, яка характеризує радіоактивний розпад, є
m = m0·akt, де m – маса речовини, яка розпалася; m0 – маса речовини в початковий момент; t – час; a і k – деякі сталі.
Примітка: доповідь бажано ілюструвати презентаційними матеріалами або відеороліками.
Задача про зміну атмосферного тиску.
Атмосферний тиск змінюється залежно від висоти h над рівнем моря за законом p = p0·ah, де p0 – атмосферний тиск на рівні моря; а – деяка стала.
Больцман отримав таку формулу для зміни атмосферного тиску залежно від висоти над рівнем моря: ![]() . (Пояснюють значення кожного символу.)
. (Пояснюють значення кожного символу.)
Задача про вакуумування.
Під час вакуумування кінцевий тиск пов’язаний з початковим тиском співвідношенням 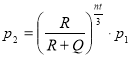 ,
,
де p2 – кінцевий тиск, мм рт. ст.; р1 – початковий тиск, мм рт. ст., R – об’єм, що підлягає відкачуванню, см3; Q - об’єм газу, що відкачується за один оберт насосом, см3; n – кількість обертів насоса, об/хв.; t – час вакуумування, хв.
ІІІ група – біологи. Розкривають тему «Розмноження живих організмів».
Короткий зміст
Друге явище, яке можна виразити за допомогою показникової функції, є розмноження живих організмів, зокрема бактерій.
Задача про розмноження бактерій.
Розмноження бактерій у певному середовищі відбувається так, що їх кількість N змінюється в часі за законом N = N0·akt, де N0 – початкова кількість бактерій при t = 0, a і k – деякі сталі.
Задача про приріст деревини.
Дерево росте так, що з часом кількість деревини збільшується за законом М = М0· akt, де М – кількість деревини у даний момент, м3; М0 – початкова кількість деревини; t – час (у роках), який відраховують з моменту, коли об’єм деревини був М0; k – деяка стала.
Обчислимо за скільки років об’єм деревини збільшиться в а разів. Поділимо обидві частини рівняння на М0, маємо ![]() , тобто akt = а. Тоді kt = 1 і
, тобто akt = а. Тоді kt = 1 і ![]() .
.
Отже, об’єм деревини збільшиться в а разів за ![]() років.
років.
ІV група – історики. Пропонує історичний екскурс про вивчення показникової функції.
Короткий зміст
Леонардо Ейлер у своїй праці «Вступ до аналізу» описав показникові і логарифмічні функції (їх будемо вивчати пізніше). Саме йому належить відкриття зв’язку між показниковою і тригонометричними функціями (пояснюють на прикладах).
Показникові функцію ![]() почали вивчати з 40-х років XVII ст. Іранський математик ал-Караджі (ХІ ст.) розглядав тричленні рівняння, квадратні відносно деякого степеня невідомого, а також рівняння, що зводяться до них діленням на степінь невідомого, тобто рівняння виду
почали вивчати з 40-х років XVII ст. Іранський математик ал-Караджі (ХІ ст.) розглядав тричленні рівняння, квадратні відносно деякого степеня невідомого, а також рівняння, що зводяться до них діленням на степінь невідомого, тобто рівняння виду ![]() .
.
VI. Формування вмінь
Робота в нових творчих групах. В кожній є представник з кожної «домашньої» групи.
Наведу типові задачі по темі. Їх кількість можна змінювати, деякі задачі можуть запропонувати творчі групи, які заздалегідь попереджені про такий вид роботи. Тоді кількість задач буде достатньою, щоб відібрати посильні для розв’язку завдання та творчі для прихильників екстріму.
-
На якій висоті знаходиться птах, якщо траєкторія польоту описується функцією
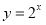 ? Розглянути для х = 3 с, х = 5 с.
? Розглянути для х = 3 с, х = 5 с.
- Закупили 1 кг зерна пшениці. Який врожай отримують через 5 років, якщо кожного року з 1 кг зерна отримують 30 кг пшениці. Задати відповідну функцію та схематично зобразити її графік.
Примітка. Графік функції ![]() буде розміщений у І координатній чверті. Початок графіка в точці (0; 1), т. я. спочатку було 1 кг зерна, початок відліку часу x = 0.
буде розміщений у І координатній чверті. Початок графіка в точці (0; 1), т. я. спочатку було 1 кг зерна, початок відліку часу x = 0.
-
Період напіврозпаду радіоактивного вуглецю 1570 років. Яка частина ядер вуглецю вже розпалася? (55%) Використати формулу
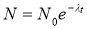 , де
, де 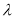 = 0,1945.
= 0,1945.
VI. Підсумки уроку
6.1. Рефлексія:
1. Які завдання не викликали труднощів при виконанні?
2. Які завдання були найважчими?
3. Які б ще теми хотіли б розглянути?
4. Яке повідомлення було найцікавішим? (Сигнальні картки) Учні, що приготували найцікавіше повідомлення отримують бонус в 1 бал.
Ці питання можна оформити, застосувавши методичний прийом «Снігова куля». Алгоритм прийому «Слово – речення – запитання – відповідь».
6.2. Оцінювання результатів навчальної діяльності учнів. Враховуємо звіт керівників груп про роботу членів групи. Використовуємо методичний прийом «Мікрофон» для отримання зворотного зв’язку з учнями.
6.3. Оголошення д/з.
Обов’язковий рівень:
- Знайти відповідь на питання «Де ще застосовують показникову функцію при вивченні фізичних явищ?»
- Скласти 3 практичні задачі на застосування показникової функції.
Підвищений рівень. Використання показникової функції в криміналістиці.

Урок № 3
Тема. Показникові рівняння
Мета: формування в учнів навичок і вмінь розв’язувати найпростіші показникові рівняння та рівняння, що зводяться до них різними способами; розвиток дослідницьких навичків учнів; виховання співдружності та наполегливості у навчанні.
Тип уроку: засвоєння нових знань і первинних умінь.
Обладнання: мультимедійний проектор, екран, опорні конспекти, карточки з тестовими завданнями, таблиці.
Хід уроку
І. Організаційний етап
Перевірка учителем готовності учнів до уроку.
ІІ. Підготовка учнів до активного свідомого засвоєння знань
2.1. Звіт помічників про наявність д/з в учнів.
2.2. Тестова перевірка знань учнів (вибірково, за бажанням учнів)
Пропонуються для виконання тести двох видів. Учитель обирає потрібний тест в залежності від рівня знань учнів, доповнює його другим варіантом. Перевіряють правильність виконання завдань за зразком на дошці.
 Тест 1. Узагальнення поняття степеня
Тест 1. Узагальнення поняття степеня
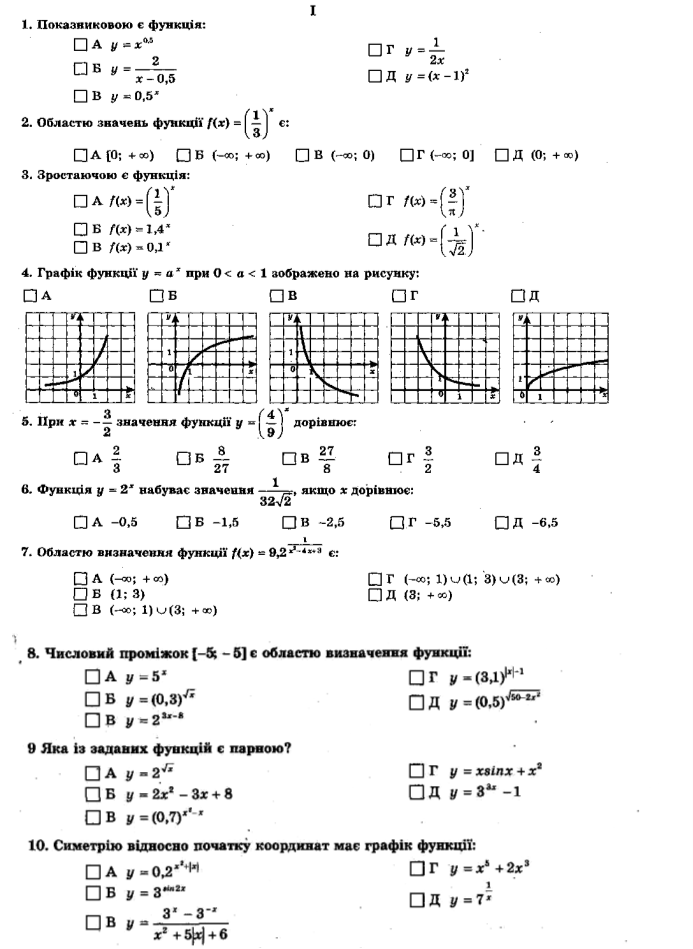 Тест 2. Показникова функція
Тест 2. Показникова функція

Відповіді до тестів
Тест 1
|
1 |
2 |
3 |
4 |
5 |
|
Б |
Б |
В |
Г |
Г |
Тест 2
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
В |
Д |
Б |
Г |
В |
Г |
Г |
Д |
Г |
Г |
В,Г,Д |
В,Г,Д |
13. Непарна
14. (3; 143)
2.3. Усні вправи
Розв’яжи рівняння:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
2.3. Питання на повторення (ланцюжком)
1) Що називається рівнянням? Типи рівнянь.
2) Загальний вигляд лінійного рівняння.
3) Кількість розв’язків лінійного рівняння.
4) Як розв’язати квадратне рівняння?
5) Які рівняння називаються ірраціональними?
6) Способи розв’язування ірраціональних рівнянь.
7) Що таке рівняння-наслідок?
8) Коли з’являються сторонні корені? Як їх виявити?
ІІІ. Формулювання теми, мети, завдань уроку
Мотивація навчальної діяльності учнів.
Розв’язування багатьох практичних задач зводиться до складання рівнянь та систем рівнянь, у яких змінна міститься в показнику степеня. Розв’язуванню деяких таких рівнянь і присвятимо цей урок.
ІV. Формування знань
4.1. Означення показникових рівнянь
Показниковими називаються рівняння, у яких змінна міститься в показнику степеня.
Наприклад:
- 4х = 64;
-
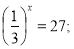
-
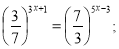
4) ![]()
5) ![]()
6) ![]() .
.
Показникові рівняння, які ми розв’язуватимемо, зводяться до найпростіших рівнянь, що мають вигляд ах = аm, а1 (якщо а = 1, то рівняння має безліч розв’язків). Із змісту степеня з дійсним показником та рівності степенів з однаковими основами випливає рівність їх показників: х = m.
4.2. Способи розв’язування показникових рівнянь
Розглянемо способи розв’язування показникових рівнянь, що безпосередньо зводяться до найпростішого виду.
1.Зведення до однієї основи
Приклад 1.
![]()
Уявимо число 0,2 степенем з основою 5.
![]() .
.
Дане рівняння можна звести до рівності степенів з основою 5.
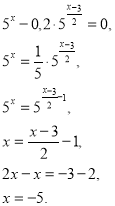
Відповідь. х = - 5.
2. Винесення спільного множника за дужки
Приклад 2.
![]() .
.
Замінимо ![]()
![]() , дістанемо рівносильне даному рівняння
, дістанемо рівносильне даному рівняння ![]() .
.
У лівій частині цього рівняння є сума степенів з однаковою основою і показниками, які відрізняються на стале число. Рівняння такого виду зводять до найпростішого винесенням у лівій частині за дужки степеня з певним показником.
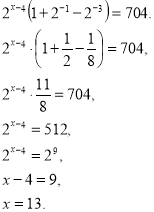
Відповідь. 13
3. Введення заміни з виходом на квадратне рівняння виду а2х + ах = b.
На відміну від попереднього рівняння винесення спільного множника за дужки у наступному рівнянні не приведе до числового значення у дужках. Розглянемо докладніше.
Приклад 3.
![]()
Спробуємо степені записати у вигляді добутків. Дістанемо:
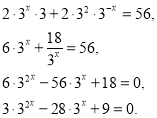
Утворилося квадратне рівняння відносно функції ![]() . Введемо заміну 3х = t,
. Введемо заміну 3х = t,
t > 0 та розв’яжемо його.
(Учні продовжують розв’язувати рівняння, коментуючи кожен крок.)
Відповідь. -1; 2.
4. Розв’язування однорідних рівнянь
Даний тип рівнянь знайомий учням з 10 класу при вивченні теми «Розв’язування тригонометричних рівнянь». Варто лише нагадати учням суть розв’язку таких рівнянь на прикладі однорідних показникових рівнянь.
Приклад 4.
![]()
Числа 4, 6, 9 можна подати у вигляді добутку простих множників 22, 23, 32. Тоді дане рівняння набере вигляду ![]() .
.
Поділимо обидві частини рівняння на 32х 0. Дістанемо:
![]() – квадратне рівняння відносно функції
– квадратне рівняння відносно функції ![]() .
.
(Учні продовжують розв’язувати рівняння самостійно.)
![]() та
та ![]() …
…
Відповідь. 0; 1.
Щоб не розгубитися при виборі способу розв’язування показникових рівнянь, звертаю увагу учнів на опорний конспект:
ПОКАЗНИКОВІ РІВНЯННЯ
 Схема рівносильних перетворень найпростіших показникових рівнянь
Схема рівносильних перетворень найпростіших показникових рівнянь
Зведення деяких показникових рівнянь до найпростіших
Розв’язування більш складних показникових рівнянь


4.3.Фізкультхвилинка
VI. Формування вмінь
6.1. Усні вправи
Звертаю увагу учнів на рівняння, які знаходяться на дошці (екрані)
- 4х = 64;
-
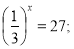
-
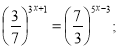
4) ![]() ;
;
5) ![]() ;
;
6) ![]() .
.
Завдання: назвати способи розв’язування кожного з рівнянь. Обґрунтувати правильність обрання способу. Після виконання заповнити таблицю:
|
Рівняння |
Спосіб розв’язування |
|
4х = 64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.2. Письмове виконання вправ. Групова робота учнів.
Завдання: розв’язати запропоновані рівняння в групах (учні самостійно обирають рівняння). Зауважуємо, що рівняння 1-3 – це рівняння початкового та середнього рівнів, 4-6 – достатнього рівня. На даному уроці не розглядаються рівняння високого рівня, враховуючи інформаційну насиченість, але за якісну роботу груп виставляємо оцінку високого рівня задля заохочення учнів у навчальній діяльності, якщо рівняння 4-6 будуть розв’язані правильно.
VII. Підсумки уроку, оголошення результатів навчання
7.1. Запитання на повторення:
1. Які рівняння називаються показниковими?
2. Як розв’язати найпростіші показникові рівняння?
3. Назвати способи розв’язування показникових рівнянь, які можна звести до найпростіших.
4. Запропонуйте спосіб розв’язування таких рівнянь:
-
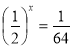 ;
;
2) ![]()
3) ![]()
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() .
.
- Оголошення д/з.
Розв’язати запропоновані рівняння, використавши опорний конспект (бажано роздрукувати на кожного учня) або конспект уроку.
Урок № 4
Тема. Системи показникових рівнянь
Мета: формування в учнів навичок і вмінь розв’язувати нескладні системи показникових рівнянь; розвиток обчислювальних навичків учнів, навичків аналізу; виховання наполегливості у навчанні.
Тип уроку: формування нових знань і первинних умінь.
Обладнання: мультимедійний проектор, екран.
Хід уроку
І. Організаційний етап
Перевірка учителем готовності учнів до уроку.
ІІ. Підготовка учнів до активного свідомого засвоєння знань
2.1. Перевірка д/з. На екран проектуємо готові відповіді до рівнянь:
1) 6; 2) 3; 3) 4; 4) 1; 5) 1; 6) 3; 7) 3; 8) 0 і 0,5; 9) 2.
Учні самостійно перевіряють правильність виконання кожного рівняння, сигналізуючи вчителю відповідною карткою. Це дасть можливість вчителю побачити на скільки складними були завдання і вчасно провести корекцію знань.
Тестова перевірка знань учнів. Завдання підібрані подібні до домашніх. (Після виконання роботи йде взаємоперевірка в парах за зразком на екрані).
 Варіант 1
Варіант 1
Варіант 2
1. Коренем рівняння ![]() є число:
є число:
|
А |
Б |
В |
Г |
Д |
|
2 |
2,5 |
3 |
0,75 |
-0,75 |
2. Розв’язками рівняння 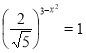 є:
є:
|
А |
Б |
В |
Г |
Д |
|
3 |
3; - 3 |
1 |
0 |
|
3. Число -3 є коренем рівняння:
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
4. Розв’язавши рівняння ![]() , отримали відповідь:
, отримали відповідь:
|
А |
Б |
В |
Г |
Д |
|
2 |
-4 |
0 |
-5 |
3 |
5. Розв’язками рівняння ![]() є числа:
є числа:
|
А |
Б |
В |
Г |
Д |
|
2 |
0,25 і -0,25 |
0; 2 |
-2 |
-2; 0 |
Відповіді
Варіант 1 Варіант 2
|
1 |
2 |
3 |
4 |
5 |
|
Б |
Б |
А |
Б |
В |
|
1 |
2 |
3 |
4 |
5 |
|
А |
Д |
Б |
Д |
А |
При перевірці та виставленні оцінок (кожне правильно виконане завдання оцінюється в 2 бали) – самооцінювання, проводимо корекцію знань учнів. Якщо при виконанні д/з не було допущено помилок, то учень має бонус в 2 бали. Тому максимальна кількість балів за тестову перевірку може досягти 12 б. При корекції знань повторюємо способи розв’язування найпростіших показникових рівнянь та рівнянь, які зводяться до найпростіших.
ІІІ. Формулювання мети і завдань уроку
Мотивація навчальної діяльності.
2.2. Усні вправи (Можна використати методичний прийом «Мікрофон», спроектувавши питання на екран)
1. Що є розв’язком системи рівнянь?
2. Що означає розв’язати систему рівнянь?
3. Скільки розв’язків може мати система рівнянь?
4. Назвіть способи розв’язування систем рівнянь.
5. Якими способами розв’язати дані системи? Назвіть розв’язки систем.
1) ![]() 2)
2) ![]() 3)
3) 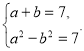
5. При яких а система ![]() має безліч розв’язків?
має безліч розв’язків?
ІV. Формування знань
4.1. Основні способи розв’язування систем показникових рівнянь
При розв’язуванні систем рівнянь використовують такі способи (називають учні):
а) спосіб підстановки (якщо потрібно, треба нагадати суть способу);
б) спосіб додавання (пригадати в яких випадках зручно використовувати даний спосіб);
в) графічний спосіб (треба зауважити на недоліки цього способу);
г) введення нової змінної задля спрощення рівнянь;
д) використання формул.
Відмічаємо, що розв’язування показникових систем рівнянь зводиться до того, щоб встановити, яке з двох рівнянь простіше. Його розв’язують в першу чергу, використовуючи способи, які були розглянуті на попередньому уроці. Після цього, аналізуючи отримані результати, повертаємось до розв’язку самої системи рівнянь.
І знову в нагоді стануть опорні конспекти для учнів з прикладами розв’язування систем показникових рівнянь. Даємо учням час (3 хв) для ознайомлення з опорними конспектами.
4.2. Фізкультхвилинка. Рухомі вправи.
1. Описати очима 2 – 3 графіка елементарних функцій, які перші спливуть у вашій уяві.
2. Описати обома руками графіки функції у = ах, які зростають (спадають).
3. Повернутись один до одного і сказати 1 приємне слово товаришу.
V. Формування вмінь
5.1. Методичний прийом «Мозковий штурм»
На екран проектуються системи показникових рівнянь. Завдання для класу: запропонувати спосіб розв’язування системи та довести його раціональність.
1) 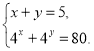
2) 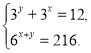
Відповідь. (1;2), (2;1)
3) 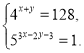
Відповідь. (2;1,5)
4) 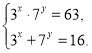
5.2. Робота в групах (по 4 особи)
Завдання: розв’язати системи показникових рівнянь.
Додаткове завдання для груп, які раніше виконають завдання:
1) 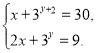
Розв’яжіть систему рівнянь та знайдіть суму х0 + у0 для одержаного розв’язку (х0;у0) системи рівнянь.
Відповідь. 4
2) Знайдіть добуток ху, якщо пара (х;у) є розв’язком системи рівнянь 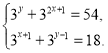
Відповідь. 3
VI. Підсумки уроку
6.1. Питання на повторення. Методичний прийом «Снігова куля» Алгоритм прийому «Слово – речення – запитання – відповідь».
6.2. Оцінювання результатів навчальної діяльності учнів. Враховуємо звіт керівників групи про роботу членів групи.
6.3. Оголошення д/з. Обов’язковий рівень:
1. Розв’яжіть систему рівнянь:
а) 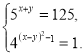 б)
б) 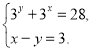 в)
в) 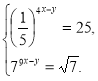
Відповідь. (0,5; 4)
г) 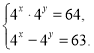
Відповідь. (3;0)
д) 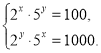
Розв’яжіть систему рівнянь та знайдіть суму х0 + у0 для одержаного розв’язку (х0;у0) системи рівнянь.
Вказівка. Слід перемножити рівняння системи і з одержаного рівняння знайти суму х + у, необхідну для запису відповіді.
Відповідь. 5
2. Знайдіть область визначення функції:
а) у = ![]() ; б)
; б) 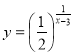 ; в)
; в) ![]() ; г)
; г) 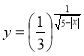 .
.
Підвищений рівень
Підготувати повідомлення про функцію у = ех. Матеріали оформити до уроку узагальнення і систематизації (урок № 6).
Додаток до уроку (для учнів)

Урок № 5
Тема. Показникові нерівності
Мета: формування в учнів навичок і вмінь розв’язувати найпростіші показникові нерівності та нерівності, що зводяться до найпростіших; розвиток навичків самоконтролю та взаємоконтролю, естетичної культури при виконанні завдань, виховання почуття співробітництва.
Тип уроку: формування нових знань і первинних умінь.
Обладнання: мультимедійний проектор, екран, таблиця «Показникові нерівності», опорні конспекти для учнів, ППЗ «Алгебра 10 клас».
Хід уроку
І. Організаційний етап
Перевіряємо готовність учнів до уроку, налаштовуємо на роботу. Консультанти звітують про наявність д/з.
Перевірка д/з
Учні звіряють за зразком на дошці (або проектуємо на екран), виставляють собі бали за виконане д/з (самооцінювання). Деякі учні працюють індивідуально.
Розв’язати систему рівнянь:
1) 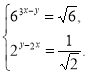 2)
2) 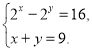 3)
3) 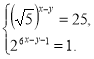
ІІ. Підготовка учнів до активного свідомого засвоєння знань
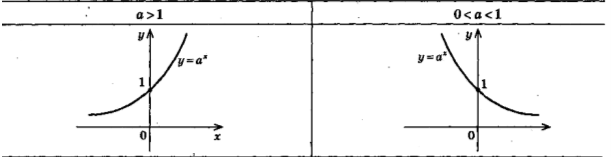
Методичний прийом «Знайди помилку» по темі «Властивості функції у = ах, якщо а![]() 1 або
1 або ![]() ».
».
На екран проектуються графіки показникових функцій (використовуємо ППЗ «Алгебра 10 клас») при різних значеннях параметра а. Учитель навмисно допускає помилки, описуючи властивості функцій, графіки яких зображені на екрані. Учні повинні знайти помилки та виправити їх. Можна на початку оголосити кількість помилок. Тоді учні уважніше аналізують кожне слово учителя.
ІІІ. Формулювання теми, мети, завдань уроку
Мотивація навчальної діяльності.
3.1. Усні вправи
Розв’язати нерівність
-
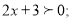 2)
2) 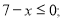
-
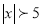 ; 4)
; 4) 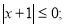
-
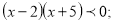 6)
6) 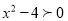 .
.
3.2.Фронтальне опитування. Гра «Відбий м’ячик»
1. Що таке переріз та об’єднання множин?
2. Як розв’язати лінійну нерівність?
3. Як розв’язати подвійну нерівність?
4. Як розв’язати нерівність методом інтервалів?
ІV. Формування знань
4.1. Означення показникових нерівностей
Показниковими називаються нерівності, у яких змінна міститься в показнику степеня.
Наприклад:
1) ![]() ; 2)
; 2) ![]() Відповідь.
Відповідь. ![]()
![]()
3) ![]() Відповідь.
Відповідь. ![]() 4)
4) ![]() ;
;
5) ![]() ; 6)
; 6) ![]() ;
;
7) ![]() ; 8)
; 8) ![]() ;
;
9) ![]() ; 10)
; 10) ![]() Відповідь.
Відповідь. ![]()
![]()
4.2. Найпростіші показникові нерівності
Найпростішими є показникові нерівності виду ![]() . Під час їх розв’язування використовують властивість монотонності показникової функції.
. Під час їх розв’язування використовують властивість монотонності показникової функції.
Функція у = ах, якщо а![]() 1 – зростає, а якщо
1 – зростає, а якщо ![]() – спадає.
– спадає.
Для а![]() 1 більшому значенню функції відповідає більший показник. Отже, для а
1 більшому значенню функції відповідає більший показник. Отже, для а![]() 1 розв’язування даної нерівності зводиться до розв’язування нерівності
1 розв’язування даної нерівності зводиться до розв’язування нерівності ![]() . Якщо
. Якщо ![]() , показникові функція спадає, тобто більшому значенню функції відповідає менший показник і для
, показникові функція спадає, тобто більшому значенню функції відповідає менший показник і для ![]() розв’язування нерівності
розв’язування нерівності ![]() зводиться до розв’язування нерівності
зводиться до розв’язування нерівності ![]() . Зверніть увагу на таблицю. (Опрацьовуємо разом таблицю, розбираємо хід розв’язання нерівностей)
. Зверніть увагу на таблицю. (Опрацьовуємо разом таблицю, розбираємо хід розв’язання нерівностей)
ПОКАЗНИКОВІ НЕРІВНОСТІ
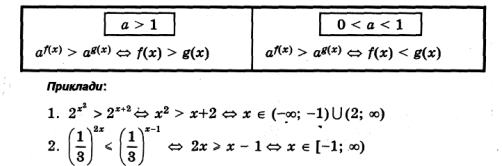
Примітка. У випадку нестрогих нерівностей знаки > і < в розв'язаннях замінюються відповідно на ≤ і ≥ .
4.3. Способи розв’язування показникових нерівностей
1. Зведення до однієї основи.
2. Винесення спільного множника за дужки.
3. Зведення до квадратної шляхом заміни.
4. Ділення обох частин нерівності на степінь.
5. Однорідні нерівності.
6. Графічний спосіб.
Учні ознайомлюються з опорним конспектом (див після конспекту уроку). Після цього обговорюємо способи розв’язування нерівностей, запропонованих для опрацювання (див. вище).
4.3.Фізкультхвилинка
VI. Формування вмінь
6.1. Письмове виконання вправ
Коментоване розв’язування нерівностей
1) ![]() .
.
Зведемо обидві частини нерівності до степенів з однаковою основою: 0,027 = (0,3)3. Тоді: ![]() Показникові функція з основою 0,3 є спадною, тому
Показникові функція з основою 0,3 є спадною, тому
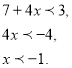
Відповідь. ![]()
2) ![]()
Винесемо за дужки спільний множник ![]() . Маємо:
. Маємо:
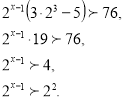
Показникові функція з основою 2 є зростаючою, тому
![]()
Відповідь. ![]()
3) ![]()
Це – однорідна нерівність. Виконаємо найпростіші перетворення:
![]() Поділимо обидві частини нерівності на
Поділимо обидві частини нерівності на ![]() . Дістанемо:
. Дістанемо:
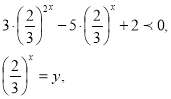
![]() , у1 = 1; у2 =
, у1 = 1; у2 = ![]() ;
;
![]()
![]()
![]()
Відповідь. ![]()
6.2. Групова робота учнів (два – чотири – разом).
Завдання: розв’язати запропоновані на початку уроку нерівності в малих групах, починаючи з роботи в парах. Якщо виникають труднощі, учні об’єднуються в групи по 4 особи. В результаті модератори груп оголошують результати, які потім виносяться на загальне обговорення.
Примітка. Нерівності 1-2 розв’язуються шляхом зведення обох частин нерівності до однієї основи, нерівності 3-4 розв’язуються способом винесення спільного множника за дужки, нерівності 5-6 – способом зведення до квадратної нерівності шляхом заміни, 7-8 – методом інтервалів, 9-10 – графічно. Це завдання високого рівня, хоча учні здатні самостійно опрацювати цей спосіб. В разі незадовільного результату учитель поспішає на допомогу.
VII. Підсумки уроку, оголошення результатів навчання
7.1. Запитання на повторення:
1. Які нерівності називаються показниковими?
2. Як розв’язати найпростіші показникові нерівності?
3. Назвати способи розв’язування показникових нерівностей, які можна звести до найпростіших.
7.2. Усні вправи
1. Представити у вигляді степеня з основою 5 вираз 0,2х.
2. Представити у вигляді добутку степенів з однаковою основою вирази 3х+1, 32 – х.
3. Подати числа 25 і![]() ;
; ![]() і
і ![]() у вигляді степенів з однаковими основами.
у вигляді степенів з однаковими основами.
4. Запропонуйте спосіб розв’язування таких нерівностей:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() Відповідь.
Відповідь. ![]()
![]()
4) ![]() ;
;
5) ![]() ; Відповідь.
; Відповідь. ![]()
![]()
6)* ![]() ; Відповідь.
; Відповідь. ![]()
![]()
7)* ![]() ;
;
8)* ![]() .
.
- Оголошення д/з.
Розв’язати запропоновані нерівності, використавши опорний конспект по темі. Нерівності 1-5 – обов’язковий рівень, 6-8 – творчий рівень.
Опорний конспект учня по темі

Урок № 6
Тема. Показникова функція
Мета: систематизувати, узагальнити та скоригувати знання учнів з теми, провести огляд понять і схем розв’язування завдань шляхом складання відповідних алгоритмів; провести корекційну роботу з метою усунення причини найтиповіших помилок; підготувати до тематичного оцінювання; розвивати логічне мислення, пам'ять, інтерес учнів до предмету, виховувати увагу, старанність, відповідальність, культуру математичної мови.
Тип уроку: узагальнення і систематизація знань.
Обладнання: ПК, проектор, екран, таблиці по графікам функцій, опорні конспекти, роздатковий матеріал.
Хід уроку
І. Організаційний етап
Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.
ІІ. Перевірка домашнього завдання
За учнівськими зразками на дошці. Звіряємо, якщо потрібно, коригуємо. Аналізуємо доцільність обраного способу розв’язування нерівності, при цьому враховуємо властивості показникової функції ![]() в залежності від значень параметра а.
в залежності від значень параметра а.
ІІІ. Формулювання мети і завдань уроку
Девіз уроку: „Алгебра щедра, вона часто дає більше, ніж у неї просять".
Мотивація навчальної діяльності учнів
Сьогодні ми з вами проведемо гру „Щасливий випадок”. На попередніх уроках ви познайомились з показниковою функцією, опрацювали її властивості, навчилися розв’язувати показникові рівняння, системи рівнянь та нерівності. Завдання сьогоднішнього уроку – узагальнити знання по темі, повторити основні способи розв′язування показникових рівнянь та нерівностей, побудову графіків показникової функції та опису її властивостей. Гра складатиметься з 5 геймів:
- Сторінки історії
- Заморочки з бочки
- Ти-мені, я-тобі
- Темна конячка
- Чорна скринька
- За крок до перемоги
ІV. Повторення і систематизація знань учнів
Клас ділиться на дві команди (можна по варіантам). Команди обирають певну назву.
Ι гейм. Історичні сторінки
Доповідь кожної команди про історію вивчення показникової функції, експоненту; історія числа е; узагальнена презентація застосування показникової функції до явищ навколишнього середовища.
ΙΙ гейм. Заморочки з бочки
Питання на повторення (учні збирали на протязі вивчення всієї теми):
- Яка функція називається показниковою?
-
Де розташований графік функції
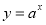 ?
?
-
Чим різняться графіки функцій
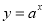 при
при 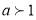 та при
та при 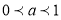 ?
?
- Що спільного у графіків таких функцій?
- Продовжити речення «Нулі функції …»
- Умова, яка накладається на параметр а.
-
Областю визначення функції
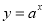 є …
є …
-
Множиною значень функції
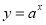 є …
є …
- Способи розв’язування показникових рівнянь (узагальнююча схема, підготовлена учнями, яка проектується на екран або вивішується на дошку).
- Способи розв’язування систем показникових рівнянь (узагальнююча схема, підготовлена учнями, яка проектується на екран або вивішується на дошку).
- Які фізичні процеси можна описати за допомогою показникової функції?
- Способи розв’язування показникових нерівностей (узагальнююча схема, підготовлена учнями, яка проектується на екран або вивішується на дошку).
- Як впливає значення параметра а на результат у показникових нерівностях?
На дошці учні розвішують підготовлені картки-поробки по показникових тотожностям. Під час опитування деякі учні можуть довести одну з означених тотожностей на дошці.
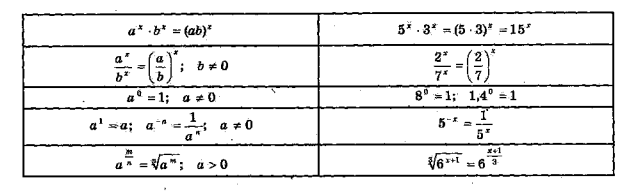 Показникові тотожності
Показникові тотожності
ΙΙΙ гейм. Ти-мені, я-тобі!
Усні вправи написані на дошці, представники кожної групи по черзі називають відповіді.
1. Які з поданих функцій є показниковими:
а) у = 2х; у = х3; у = (-5)х;
б) у = (-3)х; у = х5; у = 6х;
в) у = х7; у = (-7)3; у = 4х.
2. Порівняйте х і у:
а) 2x > 2y;
б) (1/2)x > (1/2)y;
в) 3x < 3y.
3. Розв'яжіть рівняння:
а) 2х = 16; 3х-2 = 9; ![]() ;
;
б) 3х = 81; 5х-4 = 25; ![]() ;
;![]()
в) 5х = 125; 6х-5 = 36; ![]() .
.
4. Розв'яжіть нерівності:
а) 2x > 8; 103x < 0,1;
б) 2x > 0,25; 2x < 0,25;
в) (0,5)x < 2; 5x > 0,2.
4. Методичний прийом «Так – ні»
а) 22х > 32; 22x > 25; 2x < 5; x < 2,5;
б) ![]()
![]()
![]()
в) 25x < 125; 52x < 53; 2x < 3; x < 1,5.
V. Повторення і систематизація вмінь учнів
ΙV гейм. Темна конячка
Робота в групах
Команди обирають завдання друг для друга, тобто обмінюються ними.
Кожна група отримує індивідуальне завдання.
Перша група
Розв'язати рівняння:
а) 2х + 1 + 5·2х - 2 = 104;
б) 9х + 1 + 26·3х – 3 = 0;
в) ![]() ;
;
г) 81sin2x + 81cos2x = 30.
Друга група
Розв'язати нерівності:
а) 4х – 2x > 2;
б) 7·22x + 22x + 1 < 32x + 1 + 32x;
в) ![]() < 4x + 2;
< 4x + 2;
г) ![]() < 1.
< 1.
Третя група
Розв'язати системи:
а) 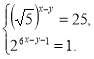 б)
б) 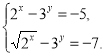 в)
в) 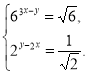
Після виконання завдань, групи обмінюються результатами, виставляють один одному оцінки. Після чого, звіряють відповіді за зразком, що проектується на дошку. При виконанні завдань дозволяється користуватися всіма опорними конспектами і таблицями.
Вводиться моніторинг складності завдань, учні відмічають, які завдання були незрозумілими, де виникли труднощі при виконанні їх. Результати заносять до таблиці.
V гейм. Чорний ящик
Методичний прийом «Зірка». Завдання: скласти по пам’яті схеми-конспекти до способів розв’язування показникових рівнянь, нерівностей, систем рівнянь. (На партах у учнів немає ніяких довідників чи опорних конспектів, схеми розв’язування, які були представлені на початку уроку прибирають. Такий прийом сприяє розвитку зорової пам’яті учнів. Після виконання звіряємо схеми за зразками.
VΙ гейм. За крок до перемоги
Підведення підсумків. Виставлення оцінок учнями (кожен собі) за роботу на кожному етапі гри.
Команді-переможцю, кожному її члену додається 1 бал за результативну співпрацю.
Рефлексія.
На дошці розміщено:
- Я почуваю себе дуже впевнено, готовий (готова) скласти тематичну атестацію.
- Я вмію творчо мислити, застосовувати набуті знання на практиці.
- Мені подобається ...
- Я задоволений, що можу так працювати на уроці.
- Я співпрацюю з вчителем який доступно передає свої знання мені.
VІ. Підсумки уроку
Оголошення д/з.
Виконати тестові завдання. Завдання 1 – 10 з вибором однієї правильної відповіді, завдання 11 – 12 з множинним вибором, завдання 13-14 з розгорнутою формою відповіді.

Відповіді до завдань
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Б |
Г |
Б |
В |
Б |
Г |
В |
Г |
Б |
Б |
А,В,Г |
Б,В |
13. (1; 3)
14. ![]()
 Матеріали для самостійної роботи учнів
Матеріали для самостійної роботи учнів

 Показникові нерівності
Показникові нерівності
Системи показникових рівнянь
1. Розв’яжіть системи рівнянь:
а) 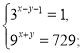 б)
б)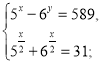 в)
в)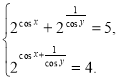
2. Розв’яжіть систему рівнянь та знайдіть суму х0 + у0 для одержаного розв’язку (х0;у0) системи рівнянь:
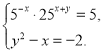
Використана література:
- Міністерство освіти і науки України. Математика 5-11 класи. Програма для загальноосвітніх навчальних закладів. -К.: Перун
2. Шкуль М. І., Слєпкань З. І., Дубинчук О. С. Підручник з алгебри і початків аналізу для 10-11 класів загальноосвітніх навчальних закладів. -Київ: Зодіак-еко, 1999.
- Колмогоров А. М., Абрамов О. М., Дудніцин Б. М. Алгебра і початки аналізу. Підручник для 10-11 класівсередньої школи. - К.: Освіта, 1994.
- Шкіль М. І., Колесник Т. В., Хмара Т. М.
Алгебра і початки аналізу. Підручник для 11 класу з поглибленим вивченням математики. - К.: Освіта, 2001.
- Авраменко М. І. Уроки алгебри і початків аналізу в 10 і 11 класах. Посібник для вчителя. – К.: Радянська школа, 1989.
- Ларічев П. О. Збірник задач з алгебри. Частина 2 для середньої школи - К.: Радянська школа, 1966.
- Гальперіна А. Р. Математика. Типові тестові завдання: Збірник. – Х.: Веста, 2010.
- Чекова Т. Г. Алгебра і початки аналізу. Успішне ЗНО: діагностичні тести, алгоритм відновлення знань, тренувальні тести, відповіді. – Х.: ТОВ «Нова тема», 2009.
- Нелін Є. П. Математика. Експрес-підготовка до ЗНО. – К.: «Літера ЛТД», 2010.
- Вечеря Т. М., Малець І. В. Алгебра. 50 тижнів до ЗНО. – Х.: ТОВ «українська книжкова мережа», 2011.
- Роєва Т. Г., Хроленко Н. Ф. Алгебра і початки аналізу в таблицях. 10 клас: Навч. Посібник. – 2-ге видання. – Х.: Країна мрій, 2002.
- Захарійченко Ю. О. Математика: Збірник тестових завдань для підготовки до зовнішнього незалежного оцінювання. – К.: Ґенеза, 2008.
1
-
-
Дякую) Дуже змістовні і чіткі уроки


про публікацію авторської розробки
Додати розробку
