Схематичний запис умови сюжетної задачі
Схематичний запис умови сюжетної задачі
Не всі вчителі математики дотримуються єдиної думки щодо доречності, необхідності та форми схематичного (короткого) запису задачі.
Звичайно, є такі задачі, для розв’язування яких достатньо зробити аналіз усно, описово.
Проте найчастіше результати попереднього аналізу задачі необхідно якимось чином зафіксувати, записати. Потрібно використати зручну, якомога компактнішу і, в разі потреби, наочну форму запису результатів аналізу задачі. Такою формою є схематичний запис задачі.
В схематичному записі доцільно використовувати різні позначення, символи, букви, малюнки, графічні моделі тощо. В ньому мають бути чітко виділені всі умови та вимоги задачі, вказані об’єкти та їх характеристики.
І, звичайно, в схематичному записі фіксуються лише тільки ті дані, які необхідні для розв’язування задачі, всі інші зазначені в сюжеті деталі відкидаються.
Є різні види схематичного запису задач. Його можна оформляти у вигляді таблиці, схеми, графічної моделі, малюнка тощо.
Схематичний запис задачі має відповідати таким вимогам:
бути зрозумілим, компактним і досить коротким (його часто так і називають «скорочений» запис задачі);
він не повинен бути трудомістким і містити багато символів, в яких дітям важко зорієнтуватись;
схематичний запис задачі – це своєрідний «місток» між аналізом задачі та її розв’язанням, з нього має логічно слідувати математична модель задачі.
Вчителю необхідно орієнтувати учнів на складання такого схематичного запису задачі, щоб він не ускладнив, а суттєво полегшив процес її розв’язання.
Розглянемо приклади оформлення схематичного запису задачі.
Задача 1.
У трьох цехах заводу працює 1274 робітники. У другому цеху на 70 робітників більше, ніж у першому, а в третьому – на 84 робітники більше, ніж у другому. Скільки робітників працює в кожному цеху?
До цієї задачі можна скласти такий схематичний запис:
![]()
![]() І – ?
І – ?
![]() ІІ – ?, на 70 > 1274
ІІ – ?, на 70 > 1274
ІІІ – ?, на 84 >
А можна такий:
![]() І – ?
І – ?
ІІ – ?, +70 1274
ІІІ – ІІ + 84
Очевидно, що якщо кількість робітників у І цеху прийняти за х, то скласти рівняння до цієї задачі легше і швидше, використовуючи другий запис:
х + (х + 70)+ (х + 70 + 84) = 1274.
Задача 2.
З пункту А виїхав велосипедист, а через 45 хв після нього в тому самому напрямку виїхала вантажівка, яка наздогнала велосипедиста на відстані 15 км від пункту А. Знайти швидкість велосипедиста і швидкість вантажівки, якщо швидкість вантажівки на 18 км/год більша за швидкість велосипедиста[11].
Автори підручника пропонують таке пояснення для розв’язування цієї задачі: «Нехай швидкість велосипедиста дорівнює х км/год, тоді швидкість вантажівки становить (х + 18) км/год. Велосипедист проїжджає 15 км за ![]() год, а вантажівка – за
год, а вантажівка – за ![]() год. Оскільки вантажівка проїхала 15 км на 45 хв, тобто на
год. Оскільки вантажівка проїхала 15 км на 45 хв, тобто на ![]() год, швидше, ніж велосипедист, то
год, швидше, ніж велосипедист, то ![]() ».
».
Це ж саме пояснення можна оформити у вигляді таблиці:
|
|
відстань |
швидкість |
час |
|
|
велосипедист |
15 км |
х км/год |
|
|
|
вантажівка |
15 км |
(х + 18) км/год |
|
|
Другий варіант є більш наочним, у ньому чіткіше прослідковуються залежності між даними та шуканими у задачі величинами.
Задача 3.
У двох мішках було 50 кг цукру. Після того, як з одного мішка взяли у 3 рази більше цукру, ніж з другого, у ньому залишилось цукру у 2 рази менше, ніж у другому. Скільки цукру залишилося в кожному мішку?
|
|
Було |
Забрали |
Стало |
|
І мішок |
50 кг |
3х кг |
|
|
ІІ мішок |
50 кг |
х кг |
(50 – х) кг |
Задача 4.
Два велосипедисти одночасно виїхали назустріч один одному. Швидкість одного з них була на 3,5 км/год більшою, ніж другого. Через 4 години вони зустрілися. З якою швидкістю рухався кожний велосипедист, якщо відстань між ними становила 102 км?
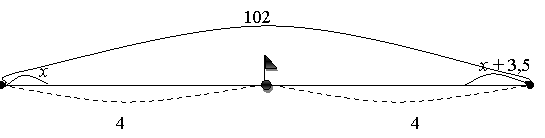
![]()
Задача 5.
Лижник проїхав відстань від турбази до села зі швидкістю 12 км/год, а повертався назад іншою дорогою, яка була на 10 км довша. Збільшивши на зворотному шляху швидкість до 15 км/год, лижник все ж витратив на цей шлях на 8 хвилин більше. Чому дорівнює відстань від турбази до села?

Задача 6.
Майстер один виконує роботу за три дні, а з учнем за 2 дні. За скільки днів виконає роботу учень самостійно?
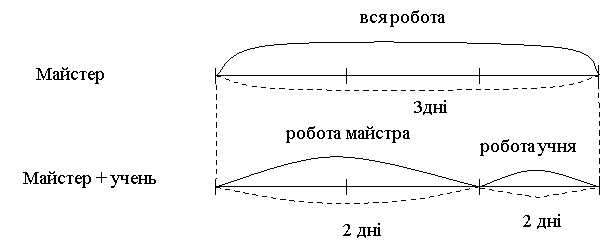
Зі схеми видно, що продуктивність учня у 2 рази менша, ніж майстра. Отже, часу для виконання всієї роботи йому потрібно у 2 рази більше. Тобто 3 ∙ 2 = 6 днів.
Іноді грамотно складена графічна модель дозволяє розв’язати не дуже просту для дітей задачу практично усно, використовуючи певні логічні міркування.
Задача 7.
З одного села одночасно в одному напрямі вирушили два пішоходи. Швидкість руху першого становила 3 км/год, а другого – 4 км/год. Через півтори години з цього села виїхав велосипедист, який наздогнав другого пішохода через 15 хв після того, як наздогнав першого. Знайти швидкість руху велосипедиста.
х год – час руху велосипедиста до зустрічі з першим пішоходом;
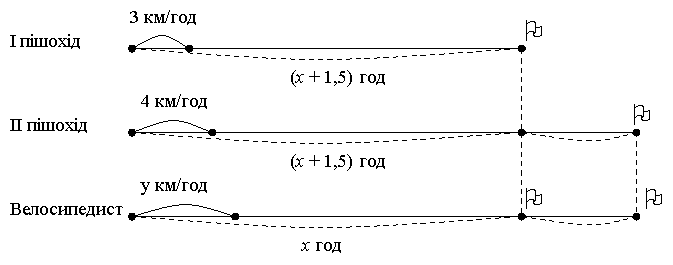 y км/год –швидкість велосипедиста
y км/год –швидкість велосипедиста
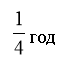


про публікацію авторської розробки
Додати розробку

