Симетрія навколо нас

Тема: Симетрія навколо нас

 

Мета: Ознайомити учнів з найпростішими властивостями симетрії відносно прямої; домогтись вміння будувати найпростіші фігури, симетричні даним відносно даних прямих та знаходити фігури, що мають осі симетрії;

формувати уявлення про симетрію в рослинному та тваринному світі, в архітектурі, літературі; сприяти більш глибокому осмисленню геометричного світу як світу

гармонії, краси і симетрії; показувати практичне застосування геометрії у житті.

тип уроку: проект

Обладнання:

Папка з матеріалами до теми “Симетрія”. Кольорова крейда. Картки.

 

Хід уроку

І. Організаційний момент

 

ІІ. Актуалізація опорних знань

Запитання

1. Які задачі на побудову ви вчили?
2. Як знайти середину відрізка?
3. Як побудувати кут, що дорівнює даному?

ІІ. Мотивація навчальної діяльності

У давнину казали, що перш ніж пізнати світ , треба пізнати себе. Давайте поглянемо на себе у дзеркало. Що ви там побачите?

Так. Ви бачите своє симетричне відображення.

Слово симетрія знайоме вам із дитинства. Наше тіло симетричне, в природі дуже багато симетричних предметів, в техніці і навіть у мові є симетрія. Що ж таке симетрія?

З токчи зору геометрії є такі види симетрії: симетрія відносно точки,  прямої та площини, осьова дзеркально-поворотна і симетрія перенесення.

Дві точки А і А₁ називаються симетричними відносно  точки О, якщо точка О є середина відрізка АА_1, що їх сполучає.

                                           А₁

                          О

       А                                         

 

     Симетрія відносно точки

 Якщо точка О переводить фігуру в себе, то фігура називається центрально-симетричною, а сама точка центром симетрії. 

 

 

 

                                   

 

 

 

Дві точки В і В₁ називаються симетричними відносно фіксованої прямої l , якщо відрізок ВВ₁ перпендикулякний прямій l , а точка їх перетину є серединою ВВ_1.

 

 

 

                             l

  В                                                 В₁                     Симетрія відносно прямої

 

 

 

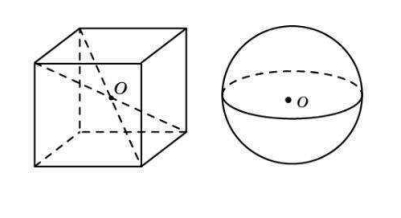
Точки А і A₁  називаються симетричними відносно площини α, якщо ця площина перпендикулярна до відрізка АА₁ і ділить його пополам. Перетворення, при якому кожна точка даної фігури відображається на точку, симетричну їй відносно площини α, називається симетрією відносно площини α. Якщо перетворення симетрії відносно площини а переводить фігуру в себе, то фігура називається симетричною відносно площини α, а площина α називається площиною симетрії.

 

 

 

Якщо в середину квадрата вписати з поворотом фінший квадрат, то це йбуде приклад дзеркально-повороьної симетрії.

Ковзної симетрією називають композицію симетрії відносно деякої прямої l і перенесення на вектор, паралельний l

 

 

Практичне завдання.

Побудувати трикутник, симетричний відносно точки та прямої.

 

Деж зустрічається симетрія у повсякденному житті?

 

Наше тіло побудовано за принципом двосторонньої симетрії.

Якщо ми подивимося уважно на фото, то помітимо, що наше обличчя зовсім не симетричне.

У кожного, зрозуміло, виявиться родимка, пасмо волосся чи якась інша деталь, порушує зовнішню симетрію. Ліве око ніколи не буває в точності таким, як правий, так і куточки рота перебувають на різній висоті, у всякому разі у більшості людей. І все ж це лише дрібні невідповідності. Ніхто не засумнівається, що зовні людина побудований симетрично: ліву руку завжди відповідає права обидві руки абсолютно однакові! Але! Тут варто зупинитися. Якби наші руки і справді були зовсім однакові, ми могли б в будь-який момент поміняти їх. Було б можливо, скажімо, шляхом трансплантації пересадити ліву долоню на праву руку, або, простіше, ліва рукавичка підходила б тоді до правої руки, але насправді це не так. Кожному відомо, що схожість між нашими руками, вухами, очима і іншими частинами тіла таке ж, як між предметом і його відображенням у дзеркалі. Серед лікарів існує думка, що однією з причин хвороб є порушення конструкції тіла. «Симетричні» тварини живуть довше, ніж «несиметричні». Симетрія - це показник здоров'я! Асиметрія особи - це показник старіння.

 

 

 

Німецький психолог Мартін Грюндль вже шість років працює з красою: вимірює її, а потім заковує в математичні формули. Два роки тому він створив формулу красивого жіночого обличчя, потім - чоловічого, тепер взявся за новий проект - цифровий еквівалент привабливого жіночого тіла. Вчені  виробляли математичний аналог краси. Її в усі часи намагалися якось пояснити, описати, а тепер вчені спробували зробити це науково. Вони не намагалися підігнати всіх під стандарт, а хотіли лише довести, що ідеальна краса, ідеальний образ, він абсолютно штучний і можливий хіба що в інтернеті. Чим симетричніше обличчя, тим привабливіша людина. Справжні люди такими не бувають.

До речі, ще одне явище симетрії – це симетрія життєвих процесів: біологічні ритми, циклічні коливання біологічних процесів і їхніх характеристик: скорочення серця, дихання, ділення клітин, обмін речовин, рухова активність.

 

Симетрія в природі

Природа - дивовижний творець і майстер. Все живе в природі має властивість симетрії.

Бджоли, однозначно, знають толк в точних науках. У всі часи люди дивувалися, наскільки, досконалі форми в медових сотах. Вони створюють справжній витвір мистецтва.

 Соняшники, так само можуть похвалитися унікальною симетрією, з якою ми знайомі як послідовністю Фібоначі. Брокколі Романеско вважається унікальним прикладом фрактальної симетрії, який має форму спіралі.

Навіть сніжинки утворюються за законами порядку. Всі вони мають різні візерунки, але кожна з них має суворої симетрією. Павутина має радіальну симетрію. Її нитки розташовані на однаковій відстані один від одного і утворюють неповторну форму

Якщо зверху подивитися на будь-яку комаху і подумки провести посередині пряму (площину), то ліві і праві половинки комах будуть однаковими і по розташуванню, і за розмірами, і за забарвленням. Адже ми ні разу не бачили, щоб у жука або бабки, у будь-якої іншої комахи лапи ліворуч були б ближче до голови, ніж праворуч, а праве крило метелика або сонечка було б більше, ніж ліве. Такого в природі не буває, інакше б комахи не змогли б літати.

  

 Властивість симетричності, властиве живій природі, людина використала у своїх досягненнях, винайшовши літак, створивши унікальні будівлі архітектури. Та й сама людина є фігурою симетричною.

    Симетрію можна побачити серед квітів. Осьову симетрію мають квітки сімейства розоцвітих, а центральну симетрію - сімейство хрестоцвітих. Симетрію можна побачити і на листі дерев.

 

 Симетрія, характерна для представників тваринного світу, називається білатеральною симетрією.

    Проте симетрія існує і там, де її не видно на перший погляд.  Таким чином, дане перетворення фігур (симетрія) увійшло в математику в результаті спостереження людини за навколишнім світом. Воно зустрічається часто і повсюдно. Тому навіть не досвідчена людина зазвичай легко вбачає симетрію у відносно простих її проявах.

Симетрія архітектурі.

Найбільш наочно видно симетрію в архітектурі. Особливо блискуче використовували симетрію в архітектурних спорудах стародавні зодчі. Причому давньогрецькі архітектори були переконані, що в своїх творах вони керуються законами, які керують природою. У свідомості давніх греків симетрія стала уособленням закономірності, доцільності, краси.

Не кажучи вже про архітектуру і скульптурі, симетрія панує в образотворчому мистецтві Стародавнього Єгипту, Стародавньої Греції та Риму, Середньовіччя і Відродження.

Симетрія об'єднує композицію. Розташування головного елемента на осі підкреслює його значимість, посилюючи підпорядкованість частин. Кожна деталь в симетричній системі існує як двійник своєї обов'язкової парі, розташованої по інший бік осі, і завдяки цьому вона може розглядатися лише як частина цілого. Значення загального тут знижує дієвість окремих елементів.

   .

 

 

Найбільш поширена в архітектурі дзеркальна симетрія. Їй підпорядковані споруди Стародавнього Єгипту і храми античної Греції, амфітеатри, терми, базиліки і тріумфальні арки римлян, палаци іцеркві Ренесансу, так само як і численні споруди сучасної архітектури. Симетрія споруди зв'язується з організацією його функцій. Проекція площини симетрії - вісь будівлі - визначає зазвичай розміщення головного входу і початок основних потоків руху. Симетрія не може бути виправданою, якщо побудови плану насильно підпорядковується несиметрична за своєю природою система життєвих процесів. Не може бути виправданням симетрія і однакове по відношенню до осі розташування нерівноцінних функцій.

     

  Центрально-осьова симетрія рідше використовувалася в історії архітектури. Їй підпорядковані античні круглі храми і побудовані в наслідування їм паркові павільйони класицизму (один з найпрекрасніших - так званий «Храм дружби», створений в Павловську за проектом Ч. Камерона в 1782 р).

Темпьетто у дворі церкви Сан-П'єтро в Римі (1502 рік, архітектор - Донато Браманте) відповідає законам центрально-осьової симетрії. Центрально-осьова симетрія визначає також форму деяких архітектурних деталей - наприклад колон і їх капітелей.

 

 

Симетрія в геометричних перетвореннях графіків функцій.

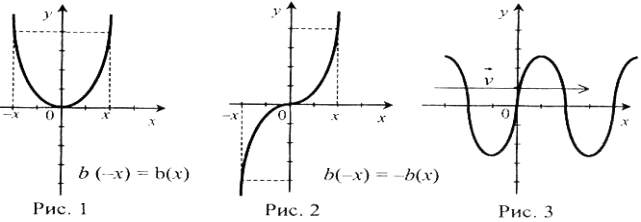
Графік парної функції симетричний щодо осі у (рис. 1), а графік непарної функції симетричний відносно початку координат (рис. 2). Графік періодичної функції має переносну симетрію уздовж осі х (рис. 3).

Крім того, всі види симетрії ми використовуємо при побудові графіків функцій за допомогою геометричних перетворень.

 

Симетрія в мистецтві.

Дзеркальна симетрія широко зустрічається в творах мистецтва примітивних цивілізацій і в стародавнього живопису. Середньовічні релігійні картини також характеризуються цим видом симетрії.

Композиція таких картин нудна, оскільки симетрія занадто очевидна.

Симетрія часто використовується і в інших видах мистецтва. У тому числі в музиці. Ряд музичних форм будується симетрично. В цьому відношенні особливо характерно рондо (рондо від фр. -Коло). В рондо музична тема багаторазово повторюється, чергуючись епізодами різного змісту. Головна тема проводиться не менше трьох разів на основній тональності, а епізоди - в інших тональностях. Це нагадує дзеркальну симетрію, основна тема служить площиною, від якої як би відображаються епізоди. Але той епізод, який раніше пролунав у високій тональності, повторюється в низькій, і навпаки.

Так накладається права рука на ліву (якщо їх не перевертати): мізинець виявляється на великому пальці. Безіменний на вказівному.

«Душа музики» - ритм - складається в правильному періодичному повторенні частин музичного твору », - писав в 1908 р відомий російський фізик Г. В. Вульф, - Правильне ж повторення - сутність симетрії».

Ми з тим більшим правом можемо докласти до музичного твору поняття симетрії, що цей твір записується за допомогою нот, т. Е. Отримуємо просторовий геометричний образ.

Гамма до мажор.

 

Композитор в своєму творі може по кілька разів повертатися до однієї і тієї ж теми, поступово розробляючи її.

Прикладом даної форми є «Рондо-капричіо» (фортепіано) Бетховена.

Букви української мови теж можна розглянути з точки зору симетрії.

Вертикальна вісь симетрії: А; М; П; Т; Ф; Ш.

Горизонтальна вісь симетрії: В; Е; 3; С; Е; Ю.

І вертикальні і горизонтальні осі симетрії: Ж; Н; П; О; X.

Ні вертикальні, ні горизонтальні осі: Б; Г; І; Й; Р; У; Ц; Ч; Щ; Я.

У російській мові є «симетричні» слова - паліндроми, які можна читати однаково в двох напрямках:

Радар, Алла, кок, піп, шалаш

На принципі симетрії ґрунтується безліч танців. Симетрія - це спокійний, незворушний, логічний і простий елемент хореографії. У безлічі номерів, де танцюристи в однаковій кількості шикуються в лінії і формують на сцені однорідну структуру, реалізується принцип симетрії.

 

Симетричними є виконання наших національних візерунків на одязі та предметах вжитку. Обов’язковою умовою в орнаменті було його повторення, зображення з боку такої самої вишиванки. У цьому вбачалось щось містичне.

 

 

 

 

 

 

 

 

 

 

 

Творче завдання.

Уявіть себе дизайнерами одягу. Добудуйте малюнок для вишивки, використовуючи симетрію відносно точки та прямої

о

 

 

 

 

 

 

о

 

 

Підсумок уроку

 

Принципи симетрії відіграють велику роль у фізиці,  математиці, хімії, біології, техніці, архітектурі, поезії, музиці. Закони природи, які керують явищами також підпорядковуються законам симетрії.

Сьогодні ми занурились у світ математики і ще раз переконалися, що цариця всіх наук на основі своїх законів вносить у життя не тільки порядок і правильність, а й гармонію та красу.

 

Домашнє завдання

 

Навести приклади симетрії у фізиці, біології, природі, мистецтві, техніці та літературі. Де ще зустрічається симетрія?

Створіть український орнамент, користуючись принципами симетрії.