Синус, косинус, тангенс і котагненс кута
Тема уроку: Синус, косинус, тангенс, котангенс кута
Мета уроку:
Предметно компетентісна мета:сформувати в учнів поняття про синус, косинус, тангенс і котангенс довільного кута, одиничне тригонометричне коло; добитися засвоєння учнями означень синуса, косинуса, тангенса й котангенса довільного кута; формувати вміння визначати sin a, cos a, tg a, ctg a, залежно від кута a
Морально етична: Виховувати морально-етичні цінності; допитливість, бажання звертатися до довідників.
Тип уроку: засвоєння нових знань.
Хід уроку
І Організаційний етап
ІІ Перевірка домашнього завдання
Актуалізація опорних знань
Домашнім завданням було повторити відомості про тригонометричні функції, що вивчались у курсі геометрії 9 класу про синус косинус і таненс кута від -0◦ до 180◦. На цьому етапі урок проводиться бесіда як були введені ці поняття. Далі з метою актуалізації знань учнів проводиться математичний диктант. Після закінчення диктанту учні виконують самоперевірку і самооцінку.
Математичний диктант
Завдання Нехай А(х;у) – точка кола радіуса R із центром у початку координат (мал 1), a – кут, утворений променем AO з додатним напрямком осі абсцис, a ∊ [0;180]. Використовуючи ці дані, дайте відповідь на такі запитання.
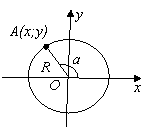
мал 1
-
Як називається відношення
 ?
?
-
Як називається відношення
 ?
?
- Чому дорівнює tg a?
- Чому дорівнює sin 45◦?
- Чому дорівнює cos 90◦?
- Чому дорівнює tg 180◦
- Чи існує кут, синус якого дорівнює 0,6?
- Чи існує кут, косинус якого дорівнює -1,5?
- Чому дорівнює cos 60◦?
- Чому дорівнює sin 60◦?
Ключ: 1.cos a 2. sin a 3. ![]() 4.
4. ![]() 5. 0 6. 0 7.Так 8.Ні 9.
5. 0 6. 0 7.Так 8.Ні 9.![]() 10.
10. ![]()
ІІІ Формулювання теми, мет і завдань уроку;
Мотивація навчальної діяльності
У курсі геометрії були обґрунтовані означення sin a, cos a, tg a для кутів від 0◦ до 180◦. Пропонується застосувати ці означення і знайти sin a, cos a, tg a для будь-яких кутів a.
IV Сприйняття й осмислення нового матеріалу
Кут у геометрії – фігура, що утворена при повороті променя ОА на площині навколо початкової точки О. Тобто можна розглядати кут як алгебраїчну величину, яка може набувати як додатних, так від’ємних значень.
Розглянувши кути повороту навколо початку координат (мал 2), при повороті проти хорду годинникової стрілки кут повороту вважають додатним, а при повороті за ходом годинникової стрілки – від’ємним.
Далі формулюється означення sin a=![]() , cos a=
, cos a=![]() , tg a=
, tg a=![]() , ctg a=
, ctg a=![]() , де х, у – координати точки В, R – радіус кола із центром у точці (0;0). Оскільки в курсі геометрії було показано, щ значення синуса, косинуса й тангенса кута a при a ∊ [0;180] залежать тільки від a і не залежать від довжини радіуса R, то і в загальному випадку sin a, cos a, tg a і сtg a залежать тільки від кута a. Якщо вважати, що R=1. Тоді sin a=у, cos a=х, tg a=
, де х, у – координати точки В, R – радіус кола із центром у точці (0;0). Оскільки в курсі геометрії було показано, щ значення синуса, косинуса й тангенса кута a при a ∊ [0;180] залежать тільки від a і не залежать від довжини радіуса R, то і в загальному випадку sin a, cos a, tg a і сtg a залежать тільки від кута a. Якщо вважати, що R=1. Тоді sin a=у, cos a=х, tg a=![]() і сtg a=
і сtg a=![]() . У цьому випадку розглянуте коло (мал 2) називають тригонометричним.
. У цьому випадку розглянуте коло (мал 2) називають тригонометричним.
Якщо початковий радіус ОА зробив повний оберт проти годинникової стрілки, то кут повороту дорівнюватиме 360◦, якщо півтора оберту, то кут повороту дорівнюватиме 540◦. Якщо початковий радіус ОА зробив два повні оберти і чверть обороту за годинниковою стрілкою, то кут повороту дорівнюватиме 2∙(-360)-90=-810.
Розглянемо радіуси ОА і ОВ (мал 3). Існує нескінченна множина кутів повороту, при яких початковий радіус ОА переходить у радіус ОВ. Нехай <АОВ=а, тоді відповідні кути повороту дорівнюватимуть а+360n, де n∊Z.
![]()
![]()
![]()
![]()
![]()
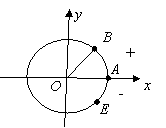

Якщо початковий радіус переходить у радіус ОВ при повороті на кут a, то залежно від того, у якій чверті буде розташований радіус ОВ, кут a називають кутом цієї чверті:
якщо 0º<α< 90º, то α – кут І чверті;
якщо 90º<α< 180º, то α – кут ІІ чверті;
якщо 180º<α< 270º, то α – кут ІІІ чверті;
якщо 270º<α< 360º, то α – кут ІV чверті;
Кути ±0º, ±90º,±180º,±270º,±360º не належать до жодної з чвертей.
Вирази sin α i cos α визначені для будь-яких α, а вираз tg α має зміст при будь-яких α крім кутів повороту ±90º,±270º,±450º і т.д. Тобто при α≠90º+180ºп, де п∊Z.
Отже кожному допустимому значенню α відповідає єдине значення sin a, cos a, сtg a, тому синус косинус, тангенс і котангенс є функціями кута α. Їх називають тригонометричними функціями.
V Первинне закріплення матеріалу
Виконання усних вправ.
-


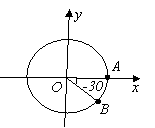
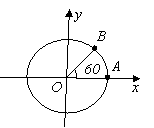
 Чому дорівнюють кути повороту, зазначені на мал 4?
Чому дорівнюють кути повороту, зазначені на мал 4?



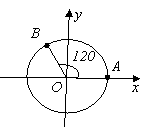
- Назвіть усі кути повороту на мал 5, при яких радіус ОА переходить ва радіус ОВ.
-
Визначте кутом якої чверті є кут α, якщо
а)α=162º б)α=310º в)α=-135º г)α=730º
Виконання письмових вправ
-
Знайдіть значення виразу
а) 2cos 60º+√3cos 30º; в)2sin30º+6cos60º-4tg45º
б) 3tg45º∙ tg60º; -
(Робота в парах)Укажіть кілька значень α, при яких :
а) sin α=1; в)sin α=0; д)ctg α =0.
б) cos α=-1; г) tg α =0; -
Дано кути повороту 770º; 480º; -50º; 1560; -240º; -310º.
Вибрати ті з них, при яких початковий радіус займе те саме положення, що й при повороті на кут:
а) α=50º; б) α=120º - Запишіть кут β=-780º у вигляді β= α+360ºп, де α ∊ (0;180), п∊Z.
VI Підбиття підсумків уроку
-
Як називається відношення
 ?
?
-
Як називається відношення
 ?
?
-
Як називається відношення
 ?
?
-
Як називається відношення
 ?
?
- У яких випадках кут повороту вважають дотатним, у яких – від’ємним?
- Заповніть пропуски 1100º=360º∙…º+…º; б)sin 540º=…; в)cos 450º=…
- Для яких кутів не мають змісту вирази tg α, ctg α?
VII Домашнє завдання
- Обчисліть 9tg 60º∙ctg 30º-sin 30º
- Знайдіть такий кут α,0º≤ α≤360º, щоб поворот початкового радіуса на цей кут збігався з поворотом на кут:
а) 420º б)-210º в)-700º
- Укажіть найбільше та найменше значення виразів:
а)1+ sin α б)2- cos α
VIII Рефлексія.


про публікацію авторської розробки
Додати розробку
