Система двох лінійних рівнянь із двома змінними та її розв'язок
Тема. Система двох лінійних рівнянь із двома змінними та її розв'язок
Мета: сформувати уявлення учнів про розв'язок системи рівнянь із двома змінними та графічний спосіб розв'язання систем лінійних рівнянь; виробити вміння: здійснювати перевірку, чи є пара (х; у) розв'язком даної системи лінійних рівнянь; використовуючи навички побудови графіка лінійного рівняння з двома змінними, розв'язувати систему двох лінійних рівнянь графічним способом.
Тип уроку: засвоєння нових знань.
Хід уроку
I. Організаційний момент
Повідомляємо учням місце уроку в темі, перевіряємо готовність до уроку.
II. Перевірка домашнього завдання
Щоб зекономити час, перевіряємо тільки вправи підвищеного рівня складності: № 1, а також № 3, який є підготовчим для сприйняття способу введення поняття «системи лінійних рівнянь із двома змінними».
III. Формулювання мети і завдань уроку
Для того щоб цей етап уроку був сприйнятий учнями свідомо, можемо поєднати його з мотиваційним етапом (або спочатку звернутись до мотиваційного аспекту)
IV. Мотивація навчальної діяльності
Свідомому розумінню необхідності знайомства з новими поняттями уроку (система лінійних рівнянь, розв'язок системи лінійних рівнянь) сприяють розв'язування конкретних задач (практичного змісту). Саме через приклади таких задач і вводяться нові поняття уроку.
V. Актуалізація опорних знань
Запитання до класу
- Що називається розв'язком рівняння з двома змінними? Чи є пара (2; 1) розв'язком рівняння 2у – х2 = -2; 3х – у = 4; х2 – у2 = 3?
- Яке рівняння з двома змінними називається лінійним? Наведіть приклад такого рівняння.
- Яка фігура є графіком лінійного рівняння ах + bу = с, в якому хоча б один з коефіцієнтів а чи b не дорівнює 0? Як розташований у координатній площині графік рівняння х = т? у = n?
VI. Вивчення нового матеріалу
Вивчення нового матеріалу можна проводити за планом:
- Задачі, що приводять до необхідності введення поняття «системи рівнянь із двома змінними».
- Поняття «системи рівняння з двома змінними».
- Розв'язання системи рівнянь із двома змінними.
- Графічний спосіб розв'язування системи (лінійних) рівнянь із двома змінними.
Питання «Система рівнянь із двома змінними» є найбільш важливим у цій темі. І поняття це формується на прикладах розв'язання задач із конкретним змістом. Але після таких задач треба все ж таки абстрагуватися і пояснити учням зміст понять «розв'язати систему рівнянь» (знайти спільні розв'язки рівнянь) та «розв'язок системи рівнянь із двома змінними» (впорядкована пара невідомих, при яких кожне рівняння системи перетворюється на правильну числову рівність, акцент на слові «кожний»). Тобто важливо неодноразово підкреслити, що розв'язок системи — це розв'язок кожного з рівнянь системи. (Бажано теоретичну частину супроводити кількома прикладами.) Щодо поняття «розв'язати систему рівнянь із двома змінними», то воно аналогічне поняттю «розв'язати рівняння».
Наступне теоретичне питання — спосіб знаходження розв'язку системи лінійних рівнянь — базується на геометричних уявленнях учнів про графік рівняння з двома змінними й дозволяє підійти до графічного способу розв'язування систем рівнянь із двома змінними, причому не тільки лінійних. У результаті пояснення учні виконують у зошиті записи, що мають вигляд конспекту 21.
|
Конспект 21 |
||||
|
Системи лінійних рівнянь із двома змінними |
||||
|
1. Означення. Якщо потрібно знайти спільні розв'язки (двох) рівнянь (із двома змінними), то кажуть, що ці рівняння утворюють систему рівнянь. |
||||
|
Позначається |
||||
|
Наприклад: |
||||
|
2. Означення. Розв'язком системи рівнянь із двома змінними називається (впорядкована) пара значень змінних, при яких кожне рівняння системи перетворюється на правильну числову рівність.
Наприклад, пара х = 2; у = 1 (2; 1) є розв'язком системи
та у =1 маємо: |
||||
|
3. Графічний спосіб розв'язування системи двох лінійних рівнянь із двома змінними: |
||||
|
1) Побудуємо графік кожного з рівнянь системи: |
||||
|
(1) у = х – 2 |
х |
0 |
2 |
|
|
у |
-2 |
0 |
||
|
(2) 3у = 2х – 2 |
х |
0 |
1 |
|
|
у |
|
0 |
||
|
Знайдемо координати точки перетину А(х; у); (х; у) – шуканий розв'язок |
||||
Виконання усних вправ
-
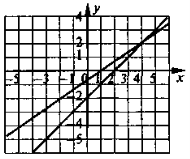
Чи є розв'язком системи
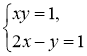 пара чисел:
пара чисел:
 1) х = 1; у = 1; 2) х = 3; у =
1) х = 1; у = 1; 2) х = 3; у = ![]() ; 3) х =
; 3) х = ![]() ; у = -2;
; у = -2;
4) х = 0; у = -1?
Звертаємо увагу учнів, що в разі, коли пара (х; у) не є розв'язком першого із рівнянь системи, для другого рівняння її вже не треба перевіряти — така пара не буде розв'язком системи (за означенням).
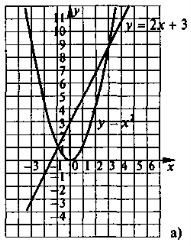
- На рисунках зображено графіки рівнянь із двома змінними, що складають системи а), б), в), г) (двох рівнянь). За графіком знайдіть розв'язки систем цих рівнянь.

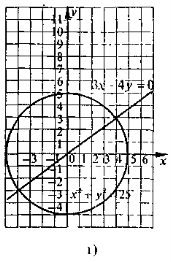
Виконання письмових вправ
- Розв'яжіть графічно систему рівнянь:
1) 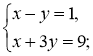 2)
2) 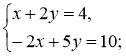 3)
3) 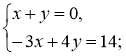 4)
4) 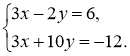
- Складіть яку-небудь систему лінійних рівнянь із двома змінними, що має розв'язок: х = -2; у = 1.
- Не виконуючи побудови, знайдіть координати точки перетину графіків функцій у = 2,5х та у = -0,5х + 12.
VII. Підсумки уроку
Контрольні запитання
- Що називається розв'язком системи двох рівнянь з двома змінними?
- Що означає розв'язати систему рівнянь?
- Як перевірити, чи є дана пара розв'язком системи?
- Як знайти розв'язок системи рівнянь графічним способом?
VIII. Домашнє завдання
№ 1. Вивчіть означення нових понять уроку; повторіть питання «Графік лінійної функції», «Взаємне розташування графіків лінійних функцій», як з лінійного рівняння виразити у через х.
№ 2. Розв'яжіть графічно систему рівнянь:
1) 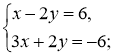 2)
2) 
№ 3. Складіть систему рівнянь, розв'язком якої є пари чисел
1) (2; 5); 2) х = 0; у = 3.
№ 4. Як розташувати в координатній площині графіки функцій:
1) у – 3х = 2 та у = 3х; 2) у = ![]() х – 1 та у =
х – 1 та у = ![]() х + 5; 3) у = 3 та у = 3х? Чому?
х + 5; 3) у = 3 та у = 3х? Чому?


про публікацію авторської розробки
Додати розробку