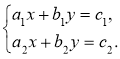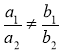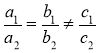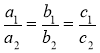Системи двох лінійних рівнянь із двома змінними та графічний спосіб розв'язування систем
Тема. Системи двох лінійних рівнянь із двома змінними та графічний спосіб розв'язування систем
Мета: засвоїти знання щодо залежності кількості розв'язків системи лінійних рівнянь від співвідношення коефіцієнтів a, b, c цих рівнянь; вироблення вмінь застосовувати названу ознаку під час графічного розв'язання систем рівнянь; подальше вдосконалювати вміння розв'язувати системи лінійних рівнянь графічним способом.
Тип уроку: засвоєння нових знань.
Хід уроку
I. Організаційний момент
- Перевірка готовності до уроку.
- План роботи (місце уроку в темі).
II. Перевірка домашнього завдання
Перевірити на уроці бажано не тільки розв'язання письмових вправ, але й теоретичну частину. Тому на початку уроку пропонуємо учням контрольні запитання (див. попередній урок), а потім проводимо інтерактивну вправу «Мікрофон». Після перевірки теоретичних знань, організуємо перевірку розв'язання письмових вправ або:
- як коментар готового розв'язання (із наступною само- або взаємоперевіркою);
- як ігровий момент «Знайди помилку».
III. Формулювання мети й завдань уроку
Після перевірки домашнього завдання (виконання письмових вправ на оволодіння теорією), маючи на увазі графічні уявлення щодо розв'язування систем лінійних рівнянь, ставимо запитання: чи завжди система двох лінійних рівнянь має розв'язок та чи завжди цей розв'язок можна знайти графічним способом. Як впевнитися в цьому, адже навіть якщо розв'язок є, але точка значно віддалена від початку відліку після побудови графіка, її можна й не побачити. Тому необхідно «винайти» точний метод для перевірки чи є взагалі в системі розв'язки, і якщо є, то скільки їх може бути.
IV. Актуалізація опорних знань
Виконання усних вправ
- Які з формул задають лінійну функцію:
1) у = 12х – 10; 2) у = 4 – 0,5х; 3) у = 15х; 4) у = х(1 – х); 5) у = 11;
6) 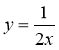 ; 7)
; 7) ![]() ?
?
-
Серед функцій: у = х + 0,5; у = -0,5х + 4; у = 5х – 1; у = 0,5x + l;
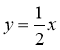 виберіть ті, графіки яких паралельні до графіка функції у = 0,5х + 1.
виберіть ті, графіки яких паралельні до графіка функції у = 0,5х + 1.
- Виразіть змінну у через змінну х у рівнянні:
1) 7х – 2у = 6; 2) у – х2 = 9; 3) 3х + 0у = 5; 4) 1,5у + 0х = 5; 5) 4х – у = 0.
V. Вивчення нового матеріалу
Дослідження числа розв'язків системи двох лінійних рівнянь з двома змінними на основі графічних уявлень і знань, властивостей графіків лінійних функцій є основною дидактичною метою уроку.
Після повторення питань: а) що є графіком лінійної функції; б) яка умова різних випадків взаємного розташування графіків двох лінійних функцій та в) як із лінійного рівняння виразити у через х (див. попередній етап уроку) учням можна запропонувати практичні завдання.
- У кожному з рівнянь системи 1) - 3) виразіть у через х та, використо-вуючи уявлення про властивості взаємного розташування графіків двох лінійних функцій, визначте (не виконуючи побудови), яке взаємне розташування графіків цих двох лінійних рівнянь:
1) 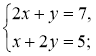 2)
2) 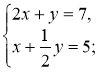 3)
3) 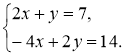
- За взаємним розташуванням графіків визначте кількість розв'язків системи.
-
Знайдіть відношення коефіцієнтів
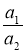 ,
, 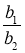 ,
, 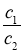 (рівнянь кожної системи) та порівняйте їх між собою.
(рівнянь кожної системи) та порівняйте їх між собою.
- Порівняйте результати виконання п. З із висновками п. 2. Сформулюй те висновок.
Після виконання та обговорення результатів узагальнюємо та коригуємо висновки й заносимо відповідні записи в зошити.
|
Конспект 22 |
|
Кількість розв'язків системи лінійних рівнянь |
|
Нехай дано систему |
|
1) Якщо |
|
2) Якщо |
|
3) Якщо |
VI. Закріплення знань, вироблення вмінь
Виконання усних вправ
-
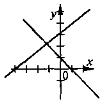
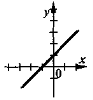
Скільки розв'язків має система, графіки рівнянь якої зображені на рис,
якщо на рис. 2) прямі паралельні, на рис. 3) збігаються?
|
|
|
|
|
1) |
2) |
3) |
-
Знайдіть відношення коефіцієнтів лінійних рівнянь системи
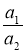 ,
, 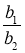 ,
, 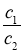 та порівняйте ці відношення.
та порівняйте ці відношення.
1)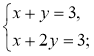 2)
2) 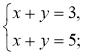 3)
3) 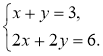
Виконання письмових вправ
- Скільки розв'язків має система рівнянь:
1) 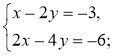 2)
2) 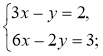 3)
3) 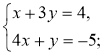 4)
4) 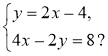
-
При яких значеннях а система
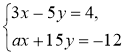
1) має нескінченно багато розв'язків? Знайдіть два такі розв'язки;
2) має один розв'язок? Знайдіть такий розв'язок;
не має розв'язків?
-
При яких значеннях коефіцієнтів а і b розв'язком системи рівнянь
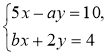 є пара чисел (2; -1)?
є пара чисел (2; -1)?
VII. Підсумки уроку
Серед рівнянь 2х + у = 3; 2х + 2у = 6 та 2х + 2у = 3 оберіть таке, щоб разом із рівнянням х + у = 3 вони утворили систему, що має:
1) один розв'язок; 2) безліч розв'язків; 3) не має розв'язків.
VIII. Домашнє завдання
№ 1. З'ясуйте, чи має система розв'язки та скільки. Для систем, що мають один розв'язок, відшукайте його, побудувавши графіки рівнянь:
1) 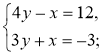 2)
2) 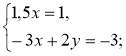 3)
3) 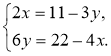
№ 2. Знайдіть які-небудь три розв'язки системи:
1) 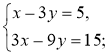 2)
2) 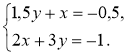
№ 3. На прямій, яка є графіком рівняння 4х + 9у = 1, узято точку, ордината якої дорівнює 1. Знайдіть абсцису цієї точки.


про публікацію авторської розробки
Додати розробку