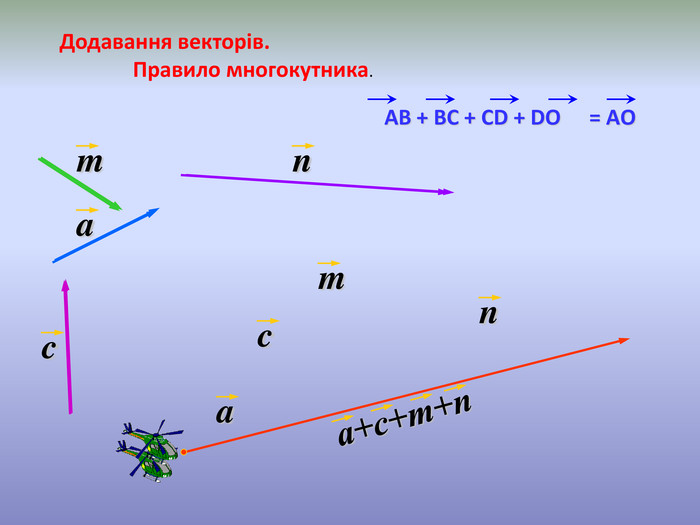
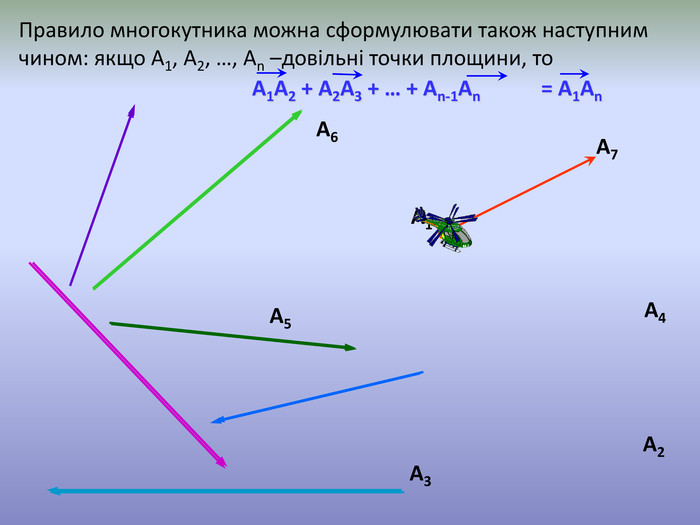
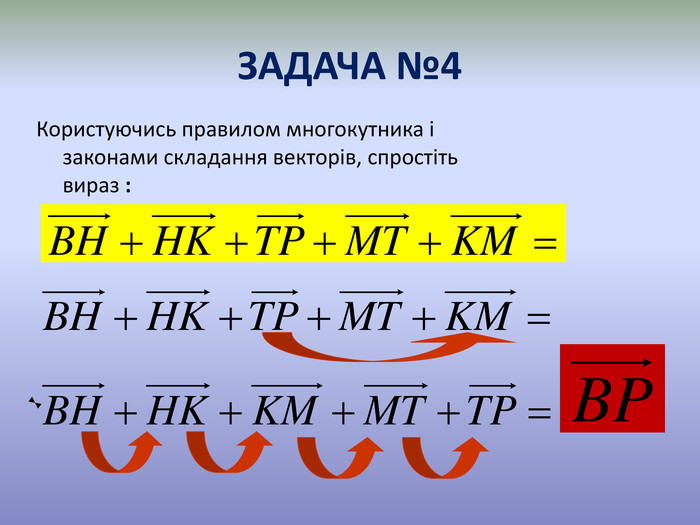
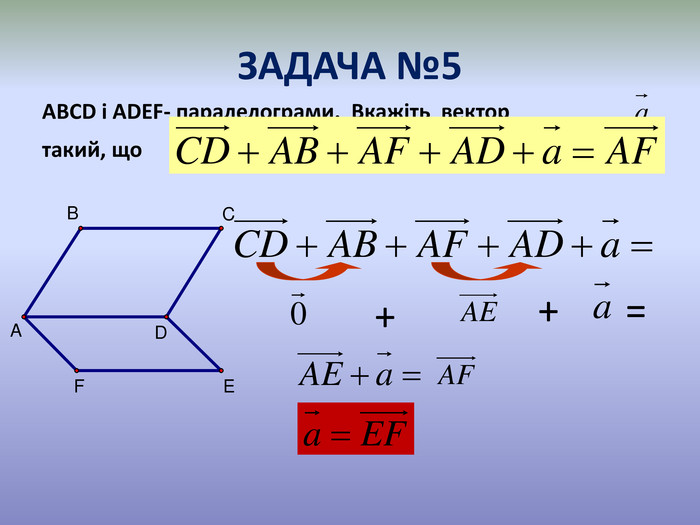
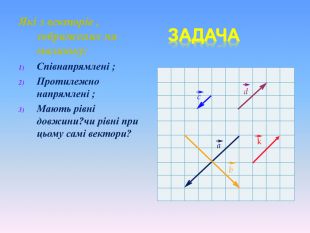
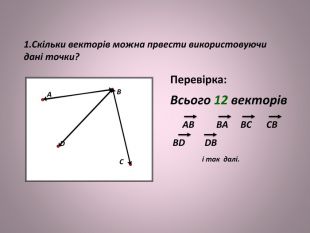
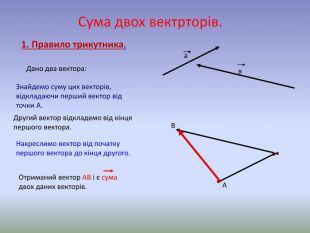
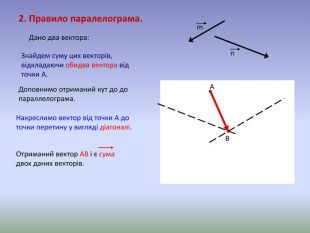
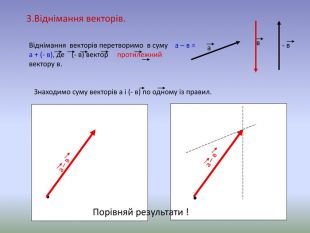
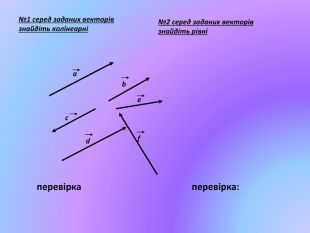
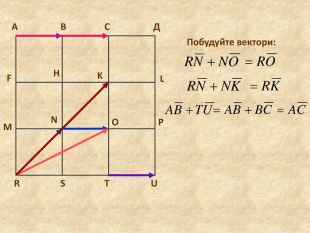
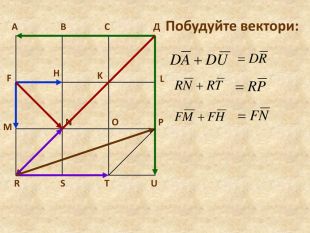
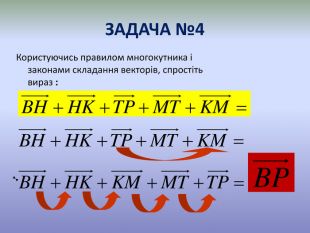
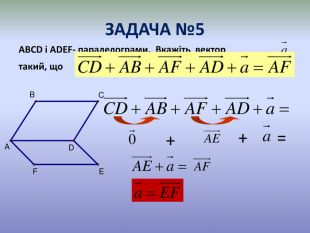
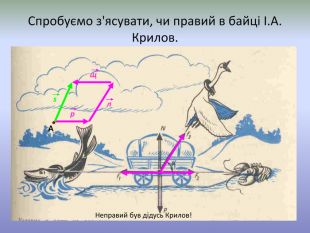
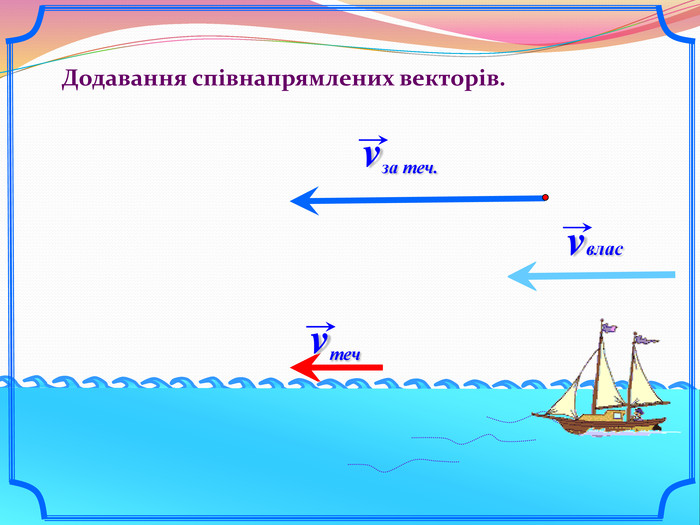
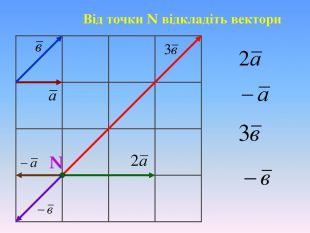
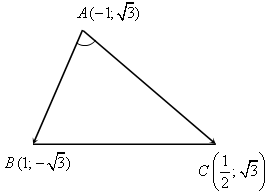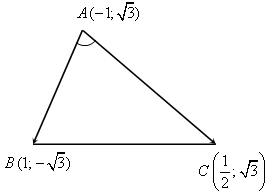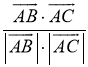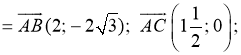Система уроків з теми "Вектори на площині"
- 1.docx docx
- 12.docx docx
- 13-14-.doc doc
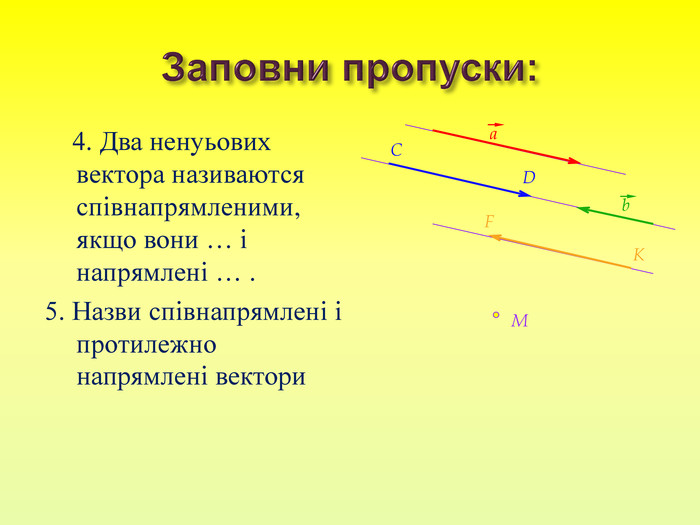
- 15.docx docx
- Показати всі файли
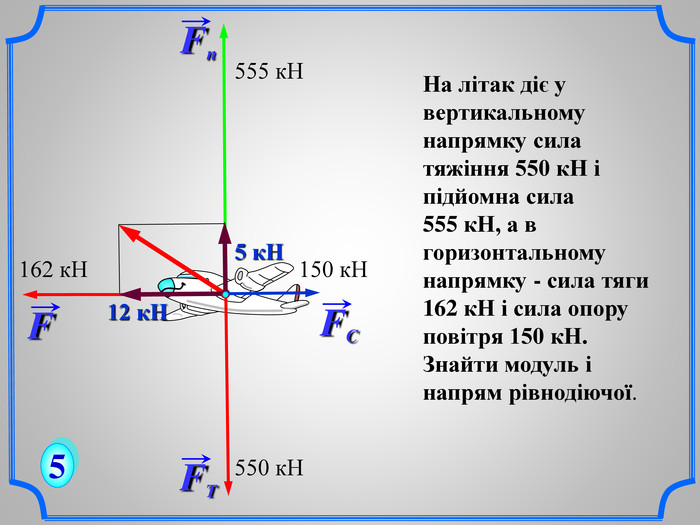
Урок № 1.
Тема. Вектор. Модуль і напрям вектор, рівність векторів .
Мета: формування поняття вектора і супутніх йому понять
(абсолютна величина вектора, напрям вектора, рівні вектори); навичок відкладання вектора від точки, сприяти розвитку мислення, усної та письмової математичної мови, уваги, виховання дисциплінованості.
Обладнання: опорні конспекти
Тип уроку: комбінований (урок ознайомлення з новим матеріалом).
Хід уроку.
І . Організаційний етап
Чого б ти не навчався,
ти навчаєшся для себе.
Петроній
ІІ. Повідомлення теми і цілей уроку, мотивація вивчення теми (Презентація №1, слайди 1-3)
Ми починаємо вивчати заключну частину теми "Декартові координати, рух і вектори на площині", яка носить назву "Вектори на площині".
При вивченні цієї теми будуть розглянуті такі питання:
1). Вектори. Арифметичні дії над векторами (додавання, віднімання, множення на число)
2). Скалярний добуток двох векторів.
3). Розкладання векторів за двома неколінеарними векторами. Орти.
На сьогоднішньому уроці будуть розглянуті наступні поняття: вектор, модуль вектора, напрям вектора, рівність векторів.
Ніколи не соромся запитувати
про те, чого не знаєш.
Арабське прислів’я
Історична довідка. (Презентація №1, слайди 4-6)
Вектор - відносно нове математичне поняття. Сам термін "вектор" (від лат Vector -. "Несучий") вперше з'явився в 1845 році у ірландського математика і астронома Вільяма Гамільтона (1805-1865) в роботах з побудови числових систем, узагальнюючих комплексні числа. Гамільтону належать терміни «скаляр», «скалярний добуток», «векторний добуток». вів німецький математик Герман Грассман (1809 - 1877). Англієць Вільям Кліффорд (1845 - 1879) зумів об'єднати два підходи в рамках загальної теорії, що включає в себе і звичайне
Майже одночасно з ним дослідження в тому ж напрямку, але з іншої точки зору числення. А остаточний вигляд воно прийняло в працях американського фізика і математика Джозайл Вілларда Гіббса (1839 - 1903), який в 1901 році опублікував великий підручник з векторного аналізу. Поняття вектора виникає там, де доводиться мати справу з об'єктами, які характеризуються величиною і напрямком.



Вільям Гамільтон Герман Грассман Джозайл Віллард Гіббс
ІІІ. Актуалізація опорних знань
Самостійна робота. В паралелограмах АВСD і А1В1С1D1 АВ=А1В1, АD=А1D1 і кут А рівний куту А1. Доведіть, що паралелограми рівні, суміщаються рухом.
![]()


![]()
![]()


 В С В1 С1
В С В1 С1
![]()
![]() А D А1 D1
А D А1 D1
Доведення .
- Сумістимо паралелограми АВСD і А1В1С1D1 так, щоб точки А і А1 співпали, а сторона АВ сумістилась зі стороню А1В1. Тоді точки В і В1 співпадуть і сторона AD суміститься зі стороню А1D1, так як кути А і А1 рівні.
2. Так як АD=А1D1, то точки D і D1 сумістяться. Звідси слідує, що сумістяться і діагоналі ВD і В1D1.
3. якщо співпадуть відрізки, то зівпадуть і їх середини, отже, точка О суміститься з точкою О1 (діагоналі паралелограма в точці перетину діляться навпіл). Значить, відрізки АО і А1О1 також сумістяться. АО=ОС і А1О1=О1С1 (за властивістю диагоналей паралелограма).
4. Оскільки відрізки АО і А1О1 співпали, можемо стверджувати, що АО=А1О1, але тоді ОС=О1С1, отже, точка С збігається з точкою С1. Тоді сторона ВС сполучиться зі стороною В1С1 і сторона СD сполучиться зі стороною С1D1. Отже, паралелограми рівні, тобто поєднуються рухом.
Фронтальне опитування
1). Які півпрямі називаються однаково напрямненими?
2). Доведіть, що якщо півпрямі а і в однаково напрямлені, і півпрямі в і з однаково напрямлені, то півпрямі а і з теж однаково напрямлені.
3). Які півпрямі називаються протилежно напрямленими?
IV. Сприйняття і осмислення матеріалу
(Під час пояснення нового матеріалу учні основні поняття записують в конспект)
|
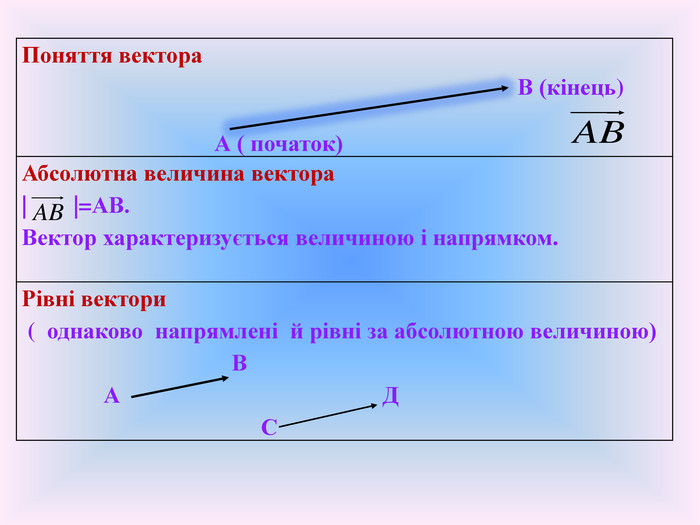
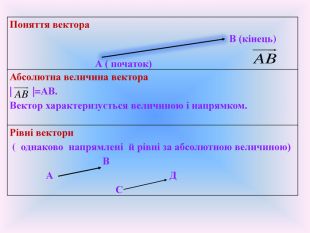
1.Поняття вектора В (кінець)
А ( початок) |
|
Абсолютна величина вектора
| Вектор характеризується величиною і напрямком. |
|
А С
|
Вектор - спрямований відрізок. Напрямок вектора визначається зазначенням його початку і кінця. На малюнку напрям вказується стрілкою
![]()
Вектор можна позначати різними способами: ![]()
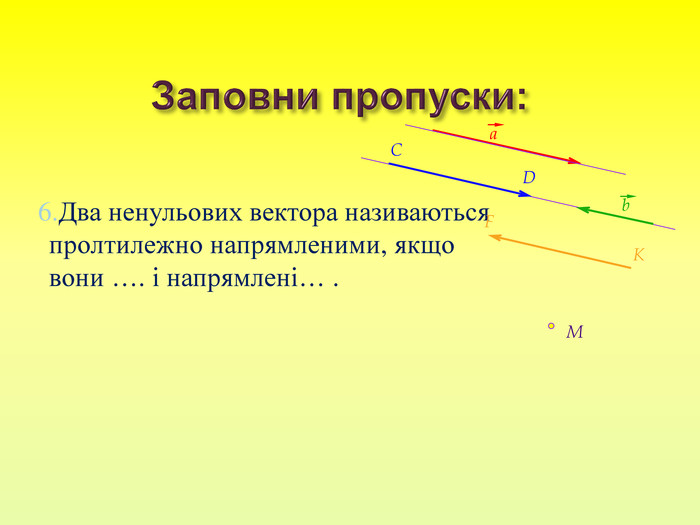
Вектори називаються однаковонапрямленими, якщо однаково напрямлені півпрямі, що містять вектор. Вектори називаються протилежнонапрямленими, якщо вони лежать на протилежно напрямлених півпрямих.
![]()
![]()
![]()
![]()
![]()
![]()
![]() і
і ![]() - однаково напрямлені;
- однаково напрямлені; ![]() і
і ![]() - протилежно напрямлені.
- протилежно напрямлені.
Вектор задається напрямком і абсолютною величиною.
Абсолютною величиною (модулем) вектора називаеться довжина відрізка, що зображає вектор: ![]() . Початок вектора може співпадати з його кінцем. Такий вектор називаеться нульовим вектором (
. Початок вектора може співпадати з його кінцем. Такий вектор називаеться нульовим вектором (![]() ).Про напрям нульового вектора не говорять. Абсолютна величина нульового вектора дорівнює нулю.
).Про напрям нульового вектора не говорять. Абсолютна величина нульового вектора дорівнює нулю.
Означення: Два вектора називаються рівними, якщо вони збігаються при паралельному перенесенні. Рівні вектори однаково напрямлені і рівні по абсолютній величині.
Властивість: Якщо вектори однаково напрямлені і рівні за абсолютною величиною, то вони рівні.
Доведення .
Нехай АВ і СD - однаково напрямлені вектори, рівні по абсолютній величині. Паралельний перенос, що переводить точку С в точку А, поєднує пів пряму СD з пів прямою АВ, тому що вони однаково напрямлені. А тому відрізки АВ і СD рівні, то точка D збігається з точкою В, тобто паралельний перенос переводить СD в АВ. Отже, АВ = СD.
![]()
![]()
![]()
![]() D В
D В
 С А
С А
Запитання . Скільки рівних векторів можна відкласти від однієї точки в заданому напрямку?
Якщо є деяка точка А, тоді від неї можна відкласти один і тількои один вектор ![]() ´, рівний вектору
´, рівний вектору ![]() .
.
![]()
![]() А
А ![]()
![]() ′
′
Існує єдиний паралельний перенос, при якому початок вектора ![]() переходить в точку А. Вектор, в який при цьому переходить вектор
переходить в точку А. Вектор, в який при цьому переходить вектор ![]() , і являеться вектором
, і являеться вектором ![]() ´.
´.
V. Формування поняття вектора, напрямки вектора, рівних векторів
Вважай нещасливим той день і ту годину,
коли ти не засвоїв нічого нового.
Давньокитайська мудрість
Діалог
№1. На прямій дано три точки: А, В, С, причому точка В лежить між А і С. Серед векторів АВ, АС, ВА і ВС назвіть однаково напрямлені і протилежно напрямлені.
№ 2. №452
№ 3. Дано паралелограм АВСD. Назвіть: а) однаково напрямлені вектори, б) протилежно напрямлені вектори, в) вектори, які мають рівні модулі; г) вектори, рівні векторам АО, ВА, ОД.
Розвязання.
а) ![]() і
і ![]() ;
; ![]() і
і ![]() ;
; ![]() і
і ![]() ,
, ![]() і
і ![]() .
.
б) ![]() і
і ![]() ,
, ![]() і
і ![]() ,
, ![]() і
і ![]() ,
, ![]() і
і ![]() ,
, ![]() і
і ![]() ,
, ![]() і
і ![]() ,
, ![]() і
і ![]() ,
, ![]() і
і ![]() .
.
в) ![]() і
і ![]() ,
, ![]() і
і ![]() .
.
г) ![]() =
=![]() ,
, ![]() =
=![]() ,
, ![]() =
=![]() .
.
В С
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() А D
А D
Колективна робота (учень розв’язує задачу біля дошки)
![]() №4. Чотирикутник АВСD - паралелограм. Доведьть рівність векторів АВ і DС.
№4. Чотирикутник АВСD - паралелограм. Доведьть рівність векторів АВ і DС.
![]()
![]()
![]() В С
В С
А D
![]() Доведення .
Доведення .
- Застосуємо до АВ паралельний перенос, при якому точка А переходить в точку D. В результаті цього переносу точка А перемещається вздовж прямої ВС, ВС||АD. Пряма АВ переходить в паралельну їй пряму, тобто в DС.
2.Отже, точка В перейде в точку С. Таким чином паралельний перенос переводить вектор ![]() в вектор
в вектор ![]() , а отже, ці вектори рівні:
, а отже, ці вектори рівні: ![]() =
=![]() .
.
№5. Відкладіть від точки С вектор, рівний вектору ![]() (із №2 ).
(із №2 ).
![]() Розвязок.
Розвязок.
![]()
![]()
![]() В С
В С
![]()
![]() А D
А D
![]() =
=![]() , так як ( В→С, А→D) і (ВС||АD).
, так як ( В→С, А→D) і (ВС||АD).
№ 6. № 454
Усні вправи
№1 Дано: АВСД — прямокутник; АВ=3; ВС=4; М- середина АВ.
Знайти: |АВ|; |ВС|; |ДС|; |МА|; |СВ|; |АС|.
№ 2 Основа АD прямокутної трапеції АВСD з прямим кутом А дорівнює 12, АВ=5 і < D= 450 . Знайти модулі векторів ![]() .
.
Робота в парах №448
V І. Підсумок уроку
![]()
![]() ? Назвіть однаково напрямлені і протилежно напрямлені вектори
? Назвіть однаково напрямлені і протилежно напрямлені вектори
![]()
![]()
![]()
![]()
![]()
![]()
![]() а в с d
а в с d
![]() p
p
VІ. Домашнє завдання
Вивчити §14 пункт 14.1- 14.2
![]() №453 (6 балів),
№453 (6 балів),
№455(9 балів), № 467
№457(12 балів)
Урок №12
Тема уроку: Діі з векторами
Мета уроку:вдосконалювати вміння учнів виконувати дії з векторами, розв’язувати задачі на застосування основних означень і теорем; розвивати логічне мислення, культуру математичної мови і записів; виховувати самостійність, інтерес до математики, взаємодовіру.
Хід уроку
Тільки той,
хто не боїться великих невдач,
зможе досягти успіху.
Дж. Кенеді
І. Організаційний етап
Постановка цілей і завдань уроку: завдання уроку : вдосконалити вміння виконувати дії з векторами, розв’язувати задачі на застосування основних означень і теорем.
ІІ. Розминка «Чи готові до уроку?»
На екрані з’являються тестові завдання із домашньої роботи у різному порядку. Учням потрібно швидко, назвавши правило, обрати відповідь із запропонованих.
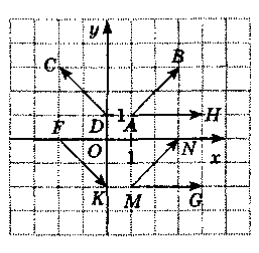 Тестова робота
Тестова робота
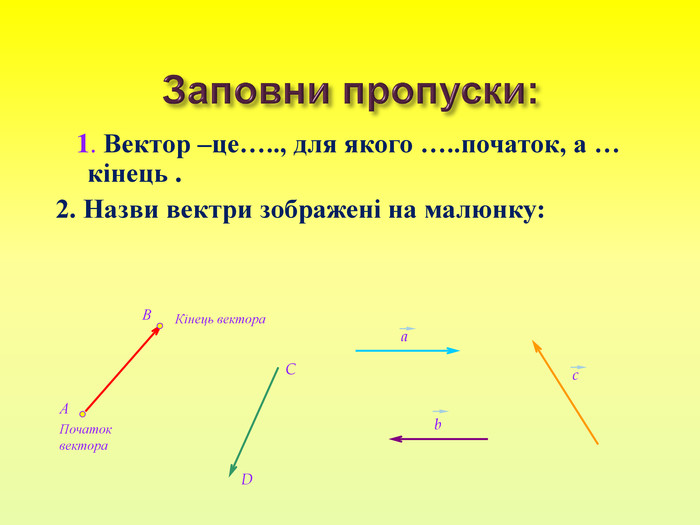
Користуючисьмалюнком,
виконайте завдання 1—6.
-
Знайдіть координати вектора
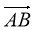 .
.
А (1; 1) Б (-2; 2) В (2; 2) Г (2; -2) -
Укажіть вектор, який дорівнює вектору
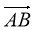 .
.
A ![]() Б
Б ![]() В
В ![]() Г
Г ![]()
-
Укажіть координати вектора
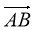 +
+ 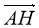 .
.
А (2; 5) Б (1; 2) В (5; 2) Г (1; -2)
-
Знайдіть
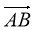 ∙
∙ 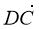 .
.
А ![]() Б 2 В 0 Г 1
Б 2 В 0 Г 1
-
При якому значенні вектори
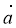 (1; -1) і
(1; -1) і 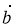 (п; 1) колінеарні?
(п; 1) колінеарні?
А Ні при яких п Б п = -1
В п = 1 Г п = ±1
- Знайдіть координати вершини D паралелограма ABCD, якщо А(0; 2), В(1; 0), С(2; 0).
А D(1; 2) Б D(2; 2) В D(1; -2) Г D(2; 1)
-
Знайдіть координати вектора
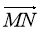 .
.
А(1; 1) Б (-2; 2) В (2; 2) Г(2; -2) -
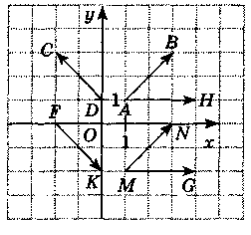 Укажіть вектор, який дорівнює вектору
Укажіть вектор, який дорівнює вектору 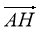 .
.
А ![]() Б
Б ![]() В
В ![]() Г
Г ![]()
-
Укажіть координати вектора
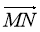 –
– 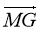 .
.
А (1; 2) Б(-1; 2) В (1; -2) Г(-1; -2)
-
Знайдіть
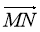 ∙
∙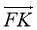 .
.
А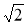 Б 2 В 0 Г 1
Б 2 В 0 Г 1
-
При якому значенні п вектори
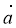 (-1; 1) і
(-1; 1) і 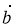 (п; -1) колінеарні?
(п; -1) колінеарні?
А n = 1 Б п = -1 В n = ±1 Г ні при яких п
-
При якому значенні п вектори
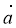 (1; -1) і
(1; -1) і 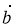 (п; 1) перпендикулярні?
(п; 1) перпендикулярні?
А Ні при яких n Б n = -1 В n = 1 Г n = ±1
ІІІ. Вдосконалення вмінь виконувати дії з векторами
Робота в парах за алгоритмом
Учням даються завдання + до окремих завдань даються детальні розв’язки, з метою, щоб учні самостійно могли перевірити правильність виконання завдань та зробити самоаналіз допущених помилок.
№ 1. Доведвіть, що для любих двох векторів ![]() і
і ![]() : (
: (![]() •
•![]() )2≤
)2≤ ![]() 2•
2•![]() 2 .
2 .
Доведення.
![]() •
•![]() =|
=| ![]() |• |
|• |![]() |cosα, тоді (
|cosα, тоді (![]() •
•![]() )2= |
)2= |![]() |2•|
|2•|![]() |2 cos2α,
|2 cos2α,
якщо -1≤сosα ≤1, тоді 0≤cos2α≤1, значить (![]()
![]() )2≤
)2≤![]() 2•
2•![]() 2.
2.
№ 2. Знайти кут між векторами ![]() (1;2),
(1;2), ![]() (1;-0,5).
(1;-0,5).
Розв’язання .
![]() •
•![]() =1•1+2•(-0,5)=0.
=1•1+2•(-0,5)=0.
![]() •
•![]() = |
= |![]() | |
| |![]() |cosα, звідси слідує, що
|cosα, звідси слідує, що
|![]() | |
| |![]() |cosα =0, cosα=0, так як
|cosα =0, cosα=0, так як ![]() ≠ 0,
≠ 0, ![]() ≠ 0, α=90˚
≠ 0, α=90˚
№3. Доведіть, що вектори ![]() (m;n) і
(m;n) і ![]() (-n;m) перпендикулярні, або обидва рівні нулю.
(-n;m) перпендикулярні, або обидва рівні нулю.
Доведення .
![]() •
•![]() = |
= |![]() | |
| |![]() | • cosα.
| • cosα. ![]() •
•![]() = -mn+mn=0. Звідси слідує, що cosα=0 або (
= -mn+mn=0. Звідси слідує, що cosα=0 або (![]() =0 і
=0 і ![]() =0),
=0), ![]() і
і ![]() перпендикулярні.
перпендикулярні.
№ 4. Дано вектори ![]() (1;0) і
(1;0) і ![]() (1;1). Знайдіть таке число λ, щоб вектор
(1;1). Знайдіть таке число λ, щоб вектор ![]() +λ
+λ![]() був перпендикулярний вектору
був перпендикулярний вектору ![]() .
.
Розв’язання .
Якщо ![]() і (
і (![]() +λ
+λ![]() ) перпендикулярні, тоді (
) перпендикулярні, тоді (![]() +λ
+λ![]() )•
)•![]() =0.
=0.
Розв’яжемо отримане рівняння : ![]() 2+λ
2+λ![]() •
•![]() =0, λ
=0, λ![]() •
•![]() = -
= -![]() 2, λ= - (
2, λ= - (![]() 2)/(
2)/( ![]() •
•![]() ).
).
![]() 2=1,
2=1, ![]() •
•![]() =1+1•0=1, λ=-1.
=1+1•0=1, λ=-1.
Додаткове завдання.
№5. Доведіть рівність ![]() 2=⌡
2=⌡![]() │2 ( скалярний квадрат вектора дорівнює квадрату його модуля)
│2 ( скалярний квадрат вектора дорівнює квадрату його модуля)
Розв’язання .
Нехай ![]() (а1;а2). Тоді |
(а1;а2). Тоді |![]() │=√а12+а22; ⌡
│=√а12+а22; ⌡![]() │2=а12+а22;
│2=а12+а22;
![]() 2=
2=![]() •
•![]() =(а1а2)•(а1а2)=а12+а22. Значить,
=(а1а2)•(а1а2)=а12+а22. Значить, ![]() 2=│
2=│![]() │2 .
│2 .
№6. Виведіть формулу квадрата суми двох векторів.
Розв’язання.
Тоді (![]() +
+![]() )2=(
)2=(![]() +
+![]() )•(
)•(![]() +
+![]() )=(
)=(![]() +
+![]() )•
)•![]() +(
+(![]() +
+![]() )•
)•![]() =
=![]()
![]() +
+![]()
![]() +
+![]()
![]() +
+![]()
![]() =
=![]() 2+2
2+2![]()
![]() +
+![]() 2.
2.
№7. Доведіть, що (![]() +
+![]() )(
)(![]() -
-![]() )=
)=![]() 2-
2-![]() 2.
2.
Обчисліть (![]() +
+![]() )(
)(![]() -
-![]() ), якщо │
), якщо │![]() │=3, │
│=3, │![]() │=5.
│=5.
Розв’язування задач біля дошки
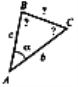
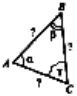
1.Розв’язати задачу № 641 на дошці і в зошитах (для кута А пояснює вчитель):
Розв’язання
|
|
1) cos A =
|
![]()
![]()
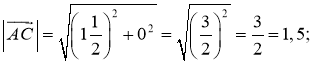
cos A = 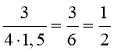 ; cos A =
; cos A = ![]() , то
, то ![]() A = 60°.
A = 60°.
2) cos B = 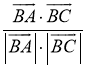 ;
; ![]()
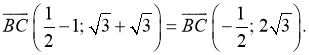
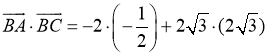 = 1 + 12 = 13;
= 1 + 12 = 13;
![]()
BC = 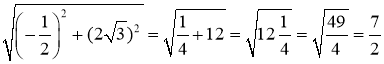 = 3,5;
= 3,5;
cos B = 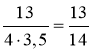 ≈ 0,9286;
≈ 0,9286; ![]() B знаходимо за таблицями Брадиса:
B знаходимо за таблицями Брадиса:
![]() B ≈ 21°47′.
B ≈ 21°47′.
3) ![]() C = 180° – 60° – 21°47′ ≈ 98°13′.
C = 180° – 60° – 21°47′ ≈ 98°13′.
відповідь: ![]() A = 60°;
A = 60°; ![]() B ≈ 21°47′;
B ≈ 21°47′; ![]() C ≈ 98°13′.
C ≈ 98°13′.
ІІІ. Підсумок уроку . «Дельта - плюс»
Учні спочатку висловлюють позитивні моменти уроку - « плюс», а потім про моменти які можна було замінити, або уникнути.цей метод навчає учнів дипломатично висловлювати свою думку, зважаючи на почуття оточуючих.
Що ми робили на уроці?
Навіщо ми це робили?
Чи досягли ви очікуваних результатів?
Чи працювали ви на завданнями разом(в групі , в парі)?
Чи узагальнювали видумки інших?
Чи доповнювали думки інших?
Чи вносили ви пропозиції, які були враховані в ході розв’язування?
ІV Домашнє завдання
§17-18 №644, №639, №654
Урок №11
Тема уроку: Діі з векторами
Мета уроку: виявити глибину учнівських знань, перевірити знання, вміння і навички учнів з теми «Вектори на площині» ; розвивати вміння мислити, застосовувати набуті знання до розв’язування вправ; виховувати самостійність, уміння самоорганізуватись.
Тип уроку: урок самостійної роботи.
Хід уроку
І. Організаційний етап
Повідомлення теми, мети і очікуваних результатів уроку. Коротка характеристика завдань самостійної роботи.
ІІ. Актуалізація опорних знань
Фронтальне опитування
З класом повторюються основні моменти теми «Вектори». Для цього дається завдання, пропонується учням відповідати по плану. Оцінюються відповіді.
1. Повторення теорії необхідної при розв'язанні задач. (проводиться у вигляді змагання між двома групами- рядами).
1) Означення вектора.
2) Координати вектора, як їх знайти.
3) Абсолютна величина вектора.
4) Сума і різниця векторів.
5) Добуток вектора на число.
6) Властивості колінеарних векторів.
7) Скалярний добуток векторів.
8) Що собою являє скалярний добуток векторів? (число чи вектор)
9) Якщо вектори перпендикулярні, що можна сказати про їх скалярний добуток? Чи вірне обернене твердження?
10) Косинус кута між векторами.
2. Задачі, які розв'язуються усно.
1) Вектор має кінець у точці А(![]() ; 0,3), а початок у точці В(0,3;
; 0,3), а початок у точці В(0,3; ![]() ).
).
Обчисліть координати даного вектора.
3) Знайдіть абсолютну величину вектора ![]() , якщо
, якщо![]() ?
?
4) Данo вектори ![]() (2; -1),
(2; -1), ![]() (-1 ; 3),
(-1 ; 3), ![]() (4; 0).
(4; 0).
Обчисліть різницю векторів ![]() +
+ ![]() і
і ![]() .
.
5) При якому значені b вектори ![]() (6; b) і
(6; b) і ![]() (5; -3) взаємно перпендикулярні
(5; -3) взаємно перпендикулярні
ІІІ. Виконання самостійної роботи
Текст контрольної роботи. Кожна правильна відповідь оцінюється в 3 бали.
Варіант 1
-
Знайдіть координати вектора
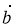 =
= 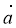 – 2
– 2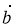 , якщо
, якщо 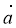 (1; 1),
(1; 1), 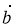 (3; 1).
(3; 1).
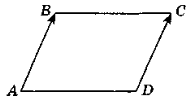
- Дано три вершини паралелограма ABCD: A(-2; 1), В(-1; 1), С(1; 1). Знайдіть координати вершини D.
-
Дано вектори
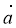 (4; 2) і
(4; 2) і 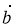 (x; -4). При якому значенні х ці вектори колінеарні?
(x; -4). При якому значенні х ці вектори колінеарні?
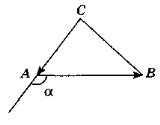
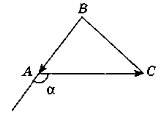
- Трикутник ABC задано координатами його вершин: А(-1; 1), В(0; 2), С(1; 1). Знайдіть зовнішній кут при вершині А.
Варіант 2
-
Знайдіть координати вектора
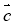 = 2
= 2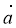 –
– 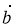 , якщо
, якщо 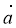 (1; 1),
(1; 1), 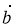 (3; 1).
(3; 1).
- Дано три вершини паралелограма ABCD: A(1; -3), В(2; -1), D(3; -3). Знайдіть координати вершини С.
-
Дано вектори
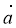 (4; 2) і
(4; 2) і 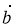 (x; -4). При якому значенні х ці вектори перпендикулярні?
(x; -4). При якому значенні х ці вектори перпендикулярні?
- Трикутник ABC задано координатами його вершин: А(3; 5), В(4; 6), С(5; 5). Знайдіть зовнішній кут при вершині А.
Варіант 3
-
Знайдіть координати вектора
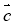 =
= 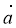 – 3
– 3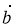 , якщо
, якщо 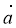 (-1; 2),
(-1; 2), 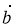 (1; -2).
(1; -2).
- Дано три вершини паралелограма ABCD: A(-4; 1), В(-1; 3), D(-2; 1). Знайдіть координати вершини С.
-
Дано вектори
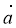 (2; 5) і
(2; 5) і 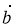 (-6; у). При якому значенні у ці вектори перпендикулярні?
(-6; у). При якому значенні у ці вектори перпендикулярні?
- Трикутник ABC задано координатами його вершин: А(1; 3), В(2; 4), С(3; 3). Знайдіть зовнішній кут при вершині А.
Варіант 4
-
Знайдіть координати вектора
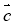 = 3
= 3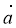 –
– 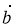 , якщо
, якщо 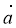 (-1; 2),
(-1; 2), 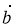 (1; -2).
(1; -2).
- Дано три вершини паралелограма ABCD: В(1; 3), С(-1;4), D(-2;2). Знайдіть координати вершини А.
-
Дано вектори
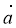 (2; 5) і
(2; 5) і 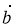 (-6; у). При якому значенні у ці вектори колінеарні?
(-6; у). При якому значенні у ці вектори колінеарні?
- Трикутник ABC задано координатами його вершин: А(0; 2), В(1; 3), С(2; 2). Знайдіть зовнішній кут при вершині А.
Відповіді та розв'язання до завдань тематичної контрольної роботи
Варіант 1
1. ![]() (1 – 2 ∙ 3; 1 – 2 ∙ 1) =
(1 – 2 ∙ 3; 1 – 2 ∙ 1) = ![]() (-5; -1). Відповідь.
(-5; -1). Відповідь. ![]() (-5; -1).
(-5; -1).
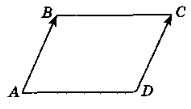
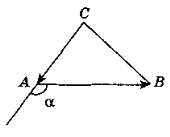
2. Нехай D(x; y), тоді ![]() (1; 0),
(1; 0), ![]() (1 – x; 1 – у) (рис. 213). Оскільки
(1 – x; 1 – у) (рис. 213). Оскільки ![]() =
= ![]() , то
, то 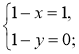
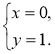 Отже, D(0; 1). Відповідь. D(0; 1).
Отже, D(0; 1). Відповідь. D(0; 1).
3. Вектори колінеарні, якщо ![]() , тоді х = -16, х = -8. Відповідь. х = -8.
, тоді х = -16, х = -8. Відповідь. х = -8.
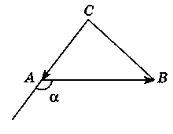
4. ![]() (-2; 0),
(-2; 0), ![]() (1; 1) (рис. 214).
(1; 1) (рис. 214). 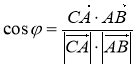 =
= 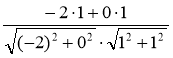 = =
= = 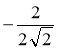 =
= ![]() =
= ![]() , звідси α = 135°. Відповідь. 135°.
, звідси α = 135°. Відповідь. 135°.
Варіант 2
1. ![]() (2 ∙ 1 – 3; 2 ∙ 1 – 1) =
(2 ∙ 1 – 3; 2 ∙ 1 – 1) = ![]() (-1; 1). Відповідь.
(-1; 1). Відповідь. ![]() (-1; 1).
(-1; 1).
2. Нехай С(х; у), тоді ![]() (1; 2),
(1; 2), ![]() (х – 3; у + 3) (рис. 215). Оскільки
(х – 3; у + 3) (рис. 215). Оскільки ![]() =
=![]() , то
, то 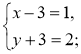
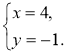 Отже, С(4; -1). Відповідь. С(4; -1).
Отже, С(4; -1). Відповідь. С(4; -1).
3. Дані вектори перпендикулярні, якщо 4 ∙ х + 2 ∙ (-4) = 0, тоді 4х – 8 = 0; 4х = 8; х = 2. Відповідь. 2.
4. ![]() (-2; 0),
(-2; 0), ![]() (1; 1), тоді (рис. 216)
(1; 1), тоді (рис. 216) 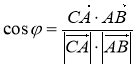 =
= 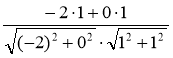 = =
= = 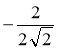 =
= ![]() =
= ![]() , звідси α = 135°. Відповідь. 135°.
, звідси α = 135°. Відповідь. 135°.
Варіант 3
1. ![]() (-1 – 3 ∙ 1; 2 – 3 ∙ (-2)) =
(-1 – 3 ∙ 1; 2 – 3 ∙ (-2)) = ![]() (-4; 8). Відповідь.
(-4; 8). Відповідь. ![]() (-4; 8).
(-4; 8).
2. Нехай С(х; у), тоді ![]() (3;2),
(3;2), ![]() (x + 2; y – 1) (рис. 217). Оскільки
(x + 2; y – 1) (рис. 217). Оскільки ![]() =
= ![]() , то
, то 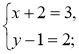
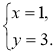 Отже, С(1; 3). Відповідь. С(1; 3).
Отже, С(1; 3). Відповідь. С(1; 3).
3. Дані вектори перпендикулярні, якщо 2 ∙ (-6) + 5 ∙ у = 0, звідси -12 + 5у = 0; 5у = 12; у = 2,4. Відповідь. 2,4.
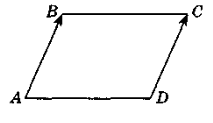
4. ![]() (-1; -1),
(-1; -1), ![]() (2; 0) (рис. 218), тоді
(2; 0) (рис. 218), тоді
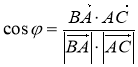 =
=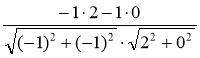 =
= 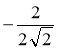 =
= ![]() =
= ![]() , звідси α = 135°. Відповідь. 135°.
, звідси α = 135°. Відповідь. 135°.
Варіант 4
1. ![]() (3 ∙ (-1) – 1; 3 ∙ 2 – (-2)) =
(3 ∙ (-1) – 1; 3 ∙ 2 – (-2)) = ![]() (-4; 8). Відповідь.
(-4; 8). Відповідь. ![]() (-4; 8).
(-4; 8).
2. Нехай А(х; у), тоді ![]() (1 – х; 3 – у),
(1 – х; 3 – у), ![]() (1; 2) (рис. 219). Оскільки
(1; 2) (рис. 219). Оскільки ![]() =
= ![]() , то
, то 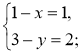
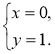 Отже, А(0; 1). Відповідь. А(0; 1).
Отже, А(0; 1). Відповідь. А(0; 1).
3. Вектори колінеарні, якщо ![]() , звідси 2у = -30; у = -15. Відповідь. -15.
, звідси 2у = -30; у = -15. Відповідь. -15.
4. ![]() (-1; -1),
(-1; -1), ![]() (2; 0) (рис. 220), тоді
(2; 0) (рис. 220), тоді
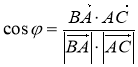 =
=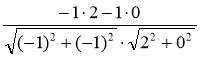 =
= 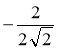 =
= ![]() =
= ![]() , звідси α = 135°. Відповідь. 135°.
, звідси α = 135°. Відповідь. 135°.
IV. Підсумок уроку
Звертається увага на завдання, які викликали забруднення.
Збираються зошити на перевірку.
V. Домашнє завдання
§16-19 (повторити основні означення,теореми і формули)
 Тестова робота
Тестова робота
Варіант 1
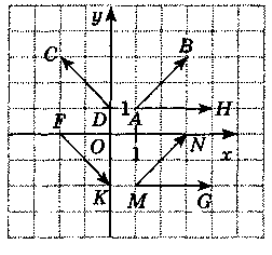
Користуючисьмалюнком,
виконайте завдання 1—6.
I рівень
-
Знайдіть координати вектора
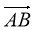 .
.
А (1; 1) Б (-2; 2) В (2; 2) Г (2; -2) -
Укажіть координати вектора -
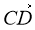 .
.
А (-2; 2) Б (2; -2); В (2; 2) Г (-2; -2)
-
Укажіть вектор, який дорівнює вектору
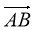 .
.
A ![]() Б
Б ![]() В
В ![]() Г
Г ![]()
II рівень
-
Укажіть координати вектора
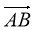 +
+ 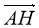 .
.
А (2; 5) Б (1; 2) В (5; 2) Г (1; -2)
-
Укажіть координати вектора
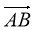 –
– 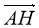 .
.
А (1; 2) Б (-1; 2) В (1; -2) Г(-1; -2)
-
Знайдіть
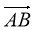 ∙
∙ 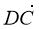 .
.
А ![]() Б 2 В 0 Г 1
Б 2 В 0 Г 1
ІІІ рівень
-
При якому значенні вектори
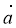 (1; -1) і
(1; -1) і 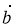 (п; 1) колінеарні?
(п; 1) колінеарні?
А Ні при яких п Б п = -1
В п = 1 Г п = ±1
-
При якому значенні п вектори
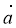 (1; 1) і
(1; 1) і 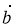 (п; 1) перпендикулярні?
(п; 1) перпендикулярні?
А п = 1 Б п = -1
В п = ±1 Г ні при яких п
- Знайдіть координати вершини D паралелограма ABCD, якщо А(0; 2), В(1; 0), С(2; 0).
А D(1; 2) Б D(2; 2) В D(1; -2) Г D(2; 1)
IV рівень
- Дано точки A(2; 1), B(3; 2), C(3; 1). Знайдіть внутрішній кут С трикутника ABC.
А 30° Б 45° В 60° Г 90°
- Знайдіть площу чотирикутника ABCD, якщо А(0; 1), В(1; 3), С(2; 1), D(1; -1).
А 2 Б 4 В 6 Г 8
-
Знайдіть кут А трикутника ABC, якщо А(0; 1), В(
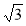 ; 2), С(
; 2), С(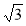 ; 1).
; 1).
А 30° Б 45° В 60° Г 90°
 Варіант 2
Варіант 2
Користуючисьмалюнком, виконайте завдання 1—6.
I рівень
-
Знайдіть координати вектора
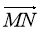 .
.
А(1; 1) Б (-2; 2) В (2; 2) Г(2; -2) -
2. Укажіть координати вектора -
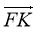 .
.
А (-2; 2) Б (2; -2); В (2; 2) Г (-2; -2) -
Укажіть вектор, який дорівнює вектору
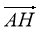 .
.
А ![]() Б
Б ![]() В
В ![]() Г
Г ![]()
II рівень
-
Укажіть координати вектора
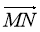 +
+ 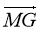 .
.
А (2; 5) Б (1; 2) В (5; 2) Г (1; -2)
-
Укажіть координати вектора
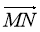 –
– 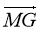 .
.
А (1; 2) Б(-1; 2) В (1; -2) Г(-1; -2)
-
Знайдіть
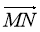 ∙
∙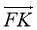 .
.
А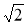 Б 2 В 0 Г 1
Б 2 В 0 Г 1
III рівень
-
При якому значенні п вектори
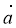 (-1; 1) і
(-1; 1) і 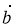 (п; -1) колінеарні?
(п; -1) колінеарні?
А n = 1 Б п = -1 В n = ±1 Г ні при яких п
-
При якому значенні п вектори
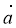 (1; -1) і
(1; -1) і 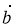 (п; 1) перпендикулярні?
(п; 1) перпендикулярні?
А Ні при яких n Б n = -1 В n = 1 Г n = ±1
- Знайдіть координати вершини А паралелограма ABCD, якщо В(1; 0), C(1; 1), D(-1; 0).
А А(2; 1) Б А(-1; -1) В А(0; 1) Г А(0; -1)
IV рівень
- Дано точки A(1; 1), В(2; 1), С(2; 2). Знайдіть внутрішній кут А трикутника ABC.
А 30° Б 45° В 60° Г 90°
- Знайдіть площу чотирикутника ABCD, якщо A(1; 1), В(2; 3), С(3; 1), D(2; -1).
А 2 Б 4 В 6 Г 8
-
Знайдіть кут В трикутника ABC, якщо А(0; -1), В(
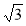 ; 0), С(
; 0), С(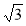 ; -1).
; -1).
А 30° Б 45° В 60° Г 90°
Відповіді до тестових завдань
|
Рівень |
Номер завдання |
Варіант 1 |
Варіант 2 |
|
І |
1 |
В |
В |
|
2 |
А |
А |
|
|
3 |
Б |
Г |
|
|
II |
4 |
В |
В |
|
5 |
Б |
Б |
|
|
6 |
В |
В |
|
|
III |
7 |
Б |
А |
|
8 |
Б |
В |
|
|
9 |
А |
Б |
|
|
IV |
10 |
Г |
Б |
|
11 |
Б |
Б |
|
|
12 |
А |
В |
Урок №13
Тема уроку: Застосування лінійних операцій над векторами.
Рішення геометричних задач векторними методами.
Мета уроку: Закріпити навички знаходження скалярного добутку векторів і кута між векторами;
Розвиток графічної культури і обчислювальних навичок школярів;
Виховання навичок навчальної праці.
Хід уроку
І. Організаційний етап.
Перевірка виконання домашнього завдання виконується на перерві (до уроку). На початку уроку робиться аналіз допущених помилок, та вказуються недоліки при розв’язанні задач. Паралельно проводиться фронтальне опитування учнів (перевіряється знання теоретичного матеріалу.)
ІІ. Актуалізація опорних знань
1) Математичний диктант
Варіант 1.
№1. Дано ромб АВСD, діагоналі якого перетинаються в точці О; АВ=ВD. Знайдіть кут між векторами: а) ![]() і
і ![]() ; б)
; б) ![]() і
і ![]() ; в)
; в) ![]() і
і ![]()
![]()
№2. Чому дорівнює кут між векторами ![]() і
і ![]() , якщо: а)
, якщо: а) ![]() •
•![]() = |
= |![]() | •|
| •| ![]() |; б)
|; б) ![]() •
•![]() = 0,5 • |
= 0,5 • |![]() | • |
| • |![]() |?
|?
№3. Скалярний квадрат вектора ![]() дорівнює 4. Знайдіть абсолютну величину вектора
дорівнює 4. Знайдіть абсолютну величину вектора ![]() .
.
№4. Чи перпендикулярні вектори ![]() (2;3) і
(2;3) і ![]() (3;-2)?
(3;-2)?
№5. Знайдіть координати і довжину вектора ![]() , якщо А(4;0), В(12;-2).
, якщо А(4;0), В(12;-2).
Варіант 2.
№1. Дано ромб АВСD, діагоналі якого перетинаються в точці О, АВ=ВD. Знайдіть кут між векторами: а) ![]() і
і ![]() ; б)
; б) ![]() і
і ![]() ; в)
; в) ![]() і
і ![]() .
.
№2. Чому дорівнює кут між векторами ![]() і
і ![]() , якщо :
, якщо :
а) ![]() •
•![]() = = - │
= = - │![]() │•│
│•│![]() │ ; б)
│ ; б) ![]() •
• ![]() =
= ![]() •│
•│![]() │ •│
│ •│ ![]() │?
│?
№3. Скалярний квадрат вектора ![]() дорівнює 9. Найдите абсолютну величину вектора
дорівнює 9. Найдите абсолютну величину вектора ![]() .
.
№4. Чи перпендикулярні вектори ![]() (-3;2) і
(-3;2) і ![]() (2;-3)?
(2;-3)?
№5. Знайдіть координати і довжину вектора ![]() , якщо С(-5;1), D(-5;-7).
, якщо С(-5;1), D(-5;-7).
Відповіді.
Варіант 1.
№1. а) 60˚; б) 60˚; в) 180˚ №2. а) 360˚; б) 60˚. №3. 4 №4. так
№5. ![]() (8;-2), │
(8;-2), │![]() │=
│=![]() .
.
Варіант 2.
№1. а) 120˚; б) 90˚; в) 120˚. №2. а) 180˚; б) 45˚. №3. 9 №4. Ні
№5. (0;-8), │![]() │=8.
│=8.
ІІІ .Тема уроку.
Мало мати хороший розум,
головне – добре його застосовувати.
Рене Декарт
Застосування інтерактивної технології «Синтез думок»
Завдання даного етапу уроку – розвинути пізнавальну активність учнів, логічне мислення.
А) робота в малих групах (3 чоловіка)
Завдання для груп однакові, кожна група висловлює свою думку щодо розв’язання задачі. Чия гіпотеза є найкращою , представник тієї групи розв’язує задачу біля дошки.
№1 Дано: А (1; –2); В (–1; 3); С (–3; 2).
а) Докведіть, що АВС – трикутник;
б) розкладіть![]() по векторам
по векторам ![]() і
і ![]() , якщо Р[AC] і |AP|:|PC| = 3:1;
, якщо Р[AC] і |AP|:|PC| = 3:1;
в) найдіть P (p1; p2); г) найдіть М (m1; m2), де М – точка перетину медіан АВС;
д) найдіть D (d1; d2), якщо точки A, B, C і D – вершини паралелограма.
Розв’язання:а) ![]() и
и ![]() – не колінеарні;
– не колінеарні;
б) ![]() =
= ![]() ;
;
в) P (–2; 1); г) М (–1; 1);
д) K – середина [BC]; K (–2; 2,5); K – середина [AD1];
г) D1 (–5; 7); ![]() ;
; ![]() ; D2 (–1; –3); В – середина [D1D3]; D3 (3; –1)]
; D2 (–1; –3); В – середина [D1D3]; D3 (3; –1)]
№2. За допомогою векторів доведемо властивість середньої лінії трапеції.
Розв’язання №1
I етап. Як у векторній формі записати, що АВСD - трапеція?
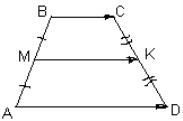
![]()
II етап. Необхідно виразити ![]() через
через ![]() и
и ![]() .
.
О ![]() і
і ![]() , звідси слідує, що
, звідси слідує, що ![]()
III етап. Так як ![]() , то
, то ![]() і
і ![]() , тобто, (MK) || (AD) и (MK) || (BC). В даному випадку,
, тобто, (MK) || (AD) и (MK) || (BC). В даному випадку, ![]() , щ. т. д.
, щ. т. д.
Розв’язання №2
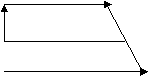 Доведемо векторну рівність
Доведемо векторну рівність ![]() =
=![]() (
(![]() +
+![]() ).
).
![]() А С
А С
М Н
В D
![]() =
=![]() ,
, ![]() =
=![]() .
.
![]() =
=![]() +
+![]() +
+![]() ,
,
![]() =
=![]() +
+![]() +
+![]() .
.
Складемо почленно ліві і праві частини:
2![]() =(
=(![]() +
+![]() )+(
)+(![]() +
+![]() )+(
)+(![]() +
+ ![]() ).
). ![]() +
+![]() =0,
=0, ![]() +
+![]() =0. 2
=0. 2![]() =
=![]() +
+![]()
![]()
![]() =
=![]() (
(![]() +
+![]() ).
).
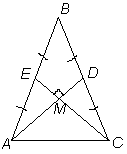 №3. У рівнобедреному трикутнику АВС з основою АС медіани, проведені до бічних сторін перпендикулярні. Знайдіть косинус кута АВС.
№3. У рівнобедреному трикутнику АВС з основою АС медіани, проведені до бічних сторін перпендикулярні. Знайдіть косинус кута АВС.
Нехай ABC = ; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
Так як (AD)(CE), то ![]() , тобто,
, тобто, ![]() ;
; ![]() .
.
№4.Теорема. Сума квадратів діагоналей паралелограма дорівнює сумі квадратів його сторін.
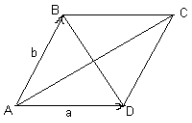
Дано: АВСD – паралелограм.
Довести: |AC|2 + |BD|2 = |AB|2 + |BC|2 + |CD|2 + |DA|2.
Доведення: ![]() ;
; ![]() ;
;
![]() |AC|2 + |BD|2 = |AB|2 + |BC|2 + |CD|2 + |DA|2, щ. т. д.
|AC|2 + |BD|2 = |AB|2 + |BC|2 + |CD|2 + |DA|2, щ. т. д.
Б)Самостійна робота
Варіант 1.
№1 (1 бал) Дано точки А(2;4), В(5;8), С(-7;-1), D(-12;-13). Знайдіть скалярний добуток векторів ![]() і
і![]() і косинус кута між ними.
і косинус кута між ними.
№2. (1 бал).Визначте, які із даних векторів, перпендикулярні:
![]() (-1;3),
(-1;3), ![]() (2;-
(2;- ![]() ),
), ![]() (-
(-![]() ;-3).
;-3).
№3 (1 бал) відомо,що А(3;2), В(-1;5), С(2;0), D(-3;-4). Знайдіть косинус кута φ між векторами ВА і DС.
№4. (3 бала) В рівнобедреному трикутнику АВС кут В дорівнює 90°, АС=![]() , ВD – медіана. Знайдіть скалярний добуток векторів
, ВD – медіана. Знайдіть скалярний добуток векторів ![]()
№5 (4 бала) Доведіть, що чотирикутник АВСD з вершинами в точках А(8;-3), В(2;5), С(10;11), D(16;3) паралелограм.![]()
Варіант 2.
![]()
![]() №1. (1 бал) Дано точки М(2;3), Р(-2;0), О(0;0), К(-5;12). Знайдіть скалярний добуток векторів МР і ОК і косинус кута між ними.
№1. (1 бал) Дано точки М(2;3), Р(-2;0), О(0;0), К(-5;12). Знайдіть скалярний добуток векторів МР і ОК і косинус кута між ними.
№2. (1 бал): Визначте, які із даних векторів, перпендикулярні: ![]()
№3 (1 бал) Відомо,що А(3;2), В(-1;5), С(2;0), D(-3;-4). Знайдіть косинус кута між векторами ![]()
№4 (3 бала). В рівносторонньому трикутнику МНР бісектриса МН=2. Знайдіть скалярний добуток векторів ![]()
№5 (4 бала) Доведіть,що чотирикутник АВСD с вершинами в точках А(4;2), В(5;7), С(-3;4), D(-4;-1) – паралелограм.
Варіант 3.
№1 (2 бала) Знайдіть кут А в трикутнику з вершинами А(1;2![]() ), В(-1;0), С(1;0).
), В(-1;0), С(1;0).
№2 (2 бала) Накресліть квадрат АВСD, діагоналі якого перетинаються в точці О. Вкажіть градусні міри кутів між векторами ![]()
№3 (6 балів) Доведіть за допомогою векторів, що сума квадратів діагоналей паралелограма дорівнює сумі квадратів всіх його сторін.
Варіант 4.
№1 (2 бала) Знайдіть кут між векторами ![]()
№2 (2 бала) Зобразіть квадрат АВСD, діагоналі якого перетинаються в точці О. Назвіть кути між векторами ![]() і знайдіть їх градусну міру.
і знайдіть їх градусну міру.
№3 ( 6 балів) Відомо, що ![]() , кут між векторами
, кут між векторами ![]() дорівнює 60°. Знайдіть
дорівнює 60°. Знайдіть ![]() .(Вказівка: Піднесіть до квадрату рівність
.(Вказівка: Піднесіть до квадрату рівність ![]() . )
. )
ІV. Підсумок уроку
Учні повторюють поняття і теореми, які були використані в ході уроку.
V. Домашнє завдання
№1. Доведіть, якщо в трикутнику АВС ![]() •(
•(![]() -
-![]() )=0, то трикутник АВС прямокутний.
)=0, то трикутник АВС прямокутний.
№2. Дано два неколінеарних вектора ![]() и
и ![]() . Побудуйте вектор 3
. Побудуйте вектор 3![]() +
+![]()
![]() .
.
Урок №14
Тема. Узагальнення і систематизація знань.
Мета: проаналізувати помилки, допущені учнями в самостійній роботі; формування практичних навичок рішення задач обов'язкового рівня, а також більш складних по темі «Вектори на площині»; сприяти розвитку пам'яті, мислення, мовлення; виховання взаємовиручки, дисциплінованості.
Обладнання: абсолютна величина вектора (табл.); скалярний добуток векторів (табл.)
Тип уроку: урок узагальнення та систематизації знань.
Хід уроку.
І. Організація дітей до роботи на уроці
ІІ. Повідомлення теми і цілей уроку
На уроці будуть проаналізовані помилки, допущені учнями в самостійній роботі; проведена корекційна робота, спрямована на вироблення навичок учнів при вирішенні завдань різного рівня складності.
ІІІ. Актуалізація опорних знань
- Що називається вектором?
- Як знайти модуль вектора?
- Що таке скалярний квадрат?
- Як знайти скалярний добуток векторів (за визначенням)?
- Чи можна визначити кут між векторами, заданими своїми координатами? Поясніть.
ІV. Розв’язування вправ на закріплення вивченого матеріалу
- Інтерактивна вправа «Мозковий штурм»
Після презентації умови задачі, яку необхідно розв’язати, учням пропонується виловити свої ідеї, коментарі, шляхи розв’язання. Усі пропозиції записуються на дошці в порядку їх оголошення без зауважень, коментарів чи запитань. Після цього обирається найраціональніше і правильне розв’язання вправи.
№1. Для векторів із №1 обчислити ![]() 2,
2, ![]() 2,
2, ![]() 2.
2.
![]() .
.
№2. Дано вектори ![]() (-1;2),
(-1;2), ![]() (2;-7),
(2;-7), ![]() (0;3),
(0;3), ![]() (0;0),
(0;0), ![]() (6;3). Знайдіть скалярний добуток векторів
(6;3). Знайдіть скалярний добуток векторів ![]() •
•![]() ,
, ![]() •
•![]() ,
, ![]() •
•![]() ,
, ![]() •
•![]() ,
, ![]() •
•![]() ,
, ![]() •
•![]() .
.
Розв’язання .
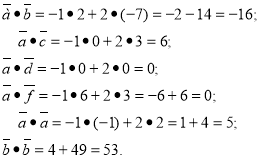
№3. Чому дорівнює кут між колінеарними векторами?
Розв’язання : Якщо колінеарні вектори однаково спрямовані, то кут між ними дорівнює 0. Якщо ці вектори протилежно спрямовані, то кут між ними дорівнює куту між рівними їм векторами зі спільним початком.
№4. На малюнку зображено рівносторонній трикутник зі стороною 6.
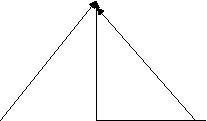 В
В
![]()
А Д С
Знайдіть скалярний добуток векторів : а) ![]() і
і ![]() ; б)
; б) ![]() і
і ![]() ; в)
; в) ![]() і
і ![]() .
.
Розв’язання .
а) ![]() б)
б) ![]()
в) ![]()
№5. Знайдіть кут між векторами :![]()
Відповідь : соs ![]()
Додаткове завдання :
№6. Чи будуть колінеарні вектори ![]()
№7. Дано вектори ![]() Знайдіть координати вектора
Знайдіть координати вектора ![]() .
.
-
Колективне розв’язування (випереджаюче навчання)
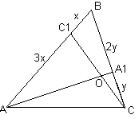
Дано: АВС; С1[AB]; |AC1|:|C1B| = 3:1;
A1[BC]; |BA1|:|A1C| = 2:1; [AA1][CC1] = O.
Знайти: |AО|:|ОА1| и |CО|:|ОC1|.
Розвязання:Яким методом ми вже вміємо вирішувати подібні завдання? [За допомогою теореми про пропорційні відрізки] Розглянемо векторний метод рішення, який дуже нагадує рішення текстових завдань у алгебрі.
Нехай ![]() ;
; ![]() , тоді
, тоді ![]() ;
; ![]() .
.
Так як ![]() , то x |
, то x | ![]() ;
;
аналогічно, y | ![]() .
.
Так як ![]() , то складаємо рівняння:
, то складаємо рівняння: ![]() .
.
По теоремі про розкладання векторів за не колінеарними векторами (![]() и
и ![]() – не колінеарні)рівняння рівносильне системі:
– не колінеарні)рівняння рівносильне системі:
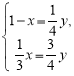
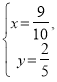 .
.
Звідси слідує, що |AО|:|ОА1| = 9:1; |CО|:|ОC1| = 2:3]
V. Підсумок уроку
Які з наступних тверджень неправильні:
а) два вектора рівні, якщо їх довжини рівні;
б) два вектори однаково спрямовані, якщо вони однаково спрямовані з третім вектором;
в) для трьох довільних точок А, В, С виконується векторна рівність ![]()
г) абсолютная величина вектора ![]() .
.
- Заповнення листа самоконтролю
- Чи досяг я мети уроку?
Так_____ Ні______
- Я працював на уроці на _________%
- Я заслуговую оцінку______________
- Чи потрібна мені допомога під час виконання домашнього завдання?
Так_____ Ні______
VІ. Домашнє завдання
Повторити §14-17
Розв’язати вправи:
№1 В трикутнику АВС вершина А(0;2), а точки М(3;5) і Р(7;4) являються серединами сторін АВ і ВС відповідно . Знайдіть координати вершини С(х;у).
№2 Знайдіть координати вектора ![]() якщо
якщо ![]() .
.
Урок №15.
Тема. Контрольна робота за темою "Вектори на площині».
Мета: оцінити знання, вміння і навички учнів за темою " Вектори на площині "; сприяти розвитку пам'яті, уваги, мислення;
виховання акуратності, дисциплінованості.
Обладнання: варіанти контрольної роботи
Тип уроку: урок контролю.
Хід уроку.
І. Організація дітей до роботи на уроці
ІІ. Повідомлення теми і цілей уроку
На уроці буде проведена контрольна робота за темою " Вектори на площині ".
ІІІ. Контрольна робота
Початковий рівень
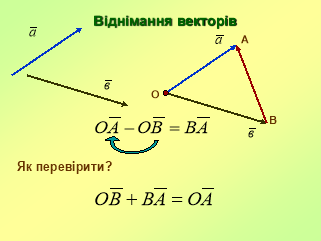
1. Дано паралелограм MNFC (рис.1), точка О- точка перетину його діагоналей. Записати:
а) всі вектори з початком у точці С; б) три пари рівних векторів;
в) три пари однаково напрямлених векторів;
г) три пари протилежно напрямлених векторів;
д) три пари рівних векторів;
 е) знайти суму векторів MN, MC, NF, FC.
е) знайти суму векторів MN, MC, NF, FC.
- Дано ромб СДNF (рис.2), G-точка перетину його діагоналей. Записати:
а) всі вектори з початком у точці F;
б) три пари рівних векторів;
в) три пари однаково напрямлених векторів;
 г) три пари протилежно напрямлених векторів;
г) три пари протилежно напрямлених векторів;
д) три пари рівних векторів;
е) знайти суму векторів MN, MC, NF, FC.
Середній рівень
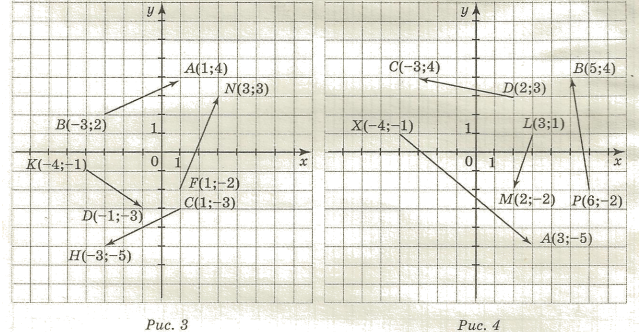
2. На рис 3 дано вектори. 2. На рис 4 дано вектори.
а) записати всі зображені вектори;
б) знайти координати всіх записаних векторів;
в) обчислити довжини всіх записаних векторів;
г) обчислити суму найменшого і найбільшого векторів;
д) три пари рівних векторів;
е) обчислити скалярний добуток найбільшого і найменшого векторів.
Достатній рівень
-
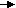 На рис.5 дано вектор n(7; -1).
На рис.5 дано вектор n(7; -1).
![]() Обчислити координати точки С та І n І
Обчислити координати точки С та І n І
-
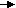
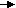
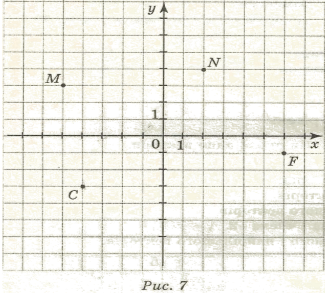
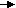 На рис. 7 дано точки M, N, F, C. Обчислити координати і модулі векторів 2MN, -3MC, 1/2FN.
На рис. 7 дано точки M, N, F, C. Обчислити координати і модулі векторів 2MN, -3MC, 1/2FN.
- На рис. 8 ∆АВС- рівносторонній. Обчислити :
-
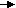
 На рис.6 дано вектор
На рис.6 дано вектор
![]() n(-7; -1). Обчислити координати точки С та І n І
n(-7; -1). Обчислити координати точки С та І n І
-
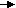
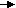
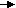 На рис. 7 дано точки M, N, F, C. Обчислити координати і модулі векторів 3NF, -2NC, 1/5MF.
На рис. 7 дано точки M, N, F, C. Обчислити координати і модулі векторів 3NF, -2NC, 1/5MF.
- На рис. 9 MNKL- прямокутник. Обчислити :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
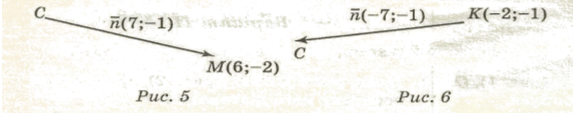 а) АМ·ВС, б)АМ·АВ, в)ВС·СМ
а) АМ·ВС, б)АМ·АВ, в)ВС·СМ
![]()
![]()
![]()
![]()
![]()
![]() а)МL·MN, б)OK·OL, в)KN·LМ
а)МL·MN, б)OK·OL, в)KN·LМ


Високий рівень
-
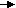
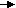
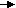
 На рис. 7 дано точки M, N, F, C. Обчислити координати і модулі векторів:
На рис. 7 дано точки M, N, F, C. Обчислити координати і модулі векторів:
а) 2MN+3CF, б)1/3(CM-NF) а) 4CN+2FM, б) 1/6(NM-FC)
7. На рис.10 дано трикутник XYZ. Обчислити зовнішній кут при вершині даного трикутника.
![]()
![]() 8. Користуючись рис.11, знайти |m-2n|.
8. Користуючись рис.11, знайти |m-2n|.
7. На рис.10 дано трикутник MNF. Довести, що даний трикутник гострокутний.
![]()
![]() 8.Користуючись рис.12, знайти |n-2m|
8.Користуючись рис.12, знайти |n-2m|
III. Підбиття підсумків уроку
 З'ясувати, які завдання викликали труднощі в учнів, та відповісти на запитання учнів.
З'ясувати, які завдання викликали труднощі в учнів, та відповісти на запитання учнів.
VІ. Домашнє завдання: підготувати презентацію на тему «Вектори».
Урок № 3
Тема. Координати вектора. Додавання векторів, його властивості.
Мета: формування поняття координат вектора, додавання і віднімання векторів, формування навичок застосування правил «трикутника» і «паралелограма» для вирішення завдань, сприяти розвитку уяви, уваги, виховання колективізму, дисциплінованості.
Обладнання: властивості додавання векторів (презентація.), формула знаходження відстані між точками (презентація.).
Тип уроку: урок ознайомлення з новим матеріалом.
Хід уроку.
І. Організаційний етап.
1. Оголошення теми і цілей уроку
Сьогодні ми познайомимося з координатами вектора, дізнаємося, як можна знайти абсолютну величину вектора, використовуючи його координати. Перед нами стоїть завдання: з'ясувати, які операції визначені для векторів і в чому особливість виконання цих операцій для векторів
ІІ. Актуалізація опорних знань
Перевірка домашнього завдання
Самостійна робота , один учень працює біля дошки
Задача: Дано вектори АВ і точка С. Відкладіть від точки С вектор, рівний вектору АВ, якщо: 1) точка С лежить на прямій АВ, 2) точка С не лежить на прямій АВ.
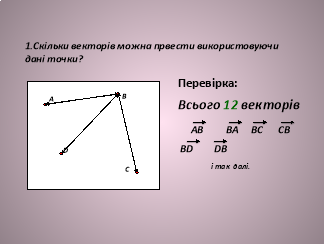 Самоперевірка (Презентація №1, слайди 14-15 ) (розв’язання Д/З проектується на екран)
Самоперевірка (Презентація №1, слайди 14-15 ) (розв’язання Д/З проектується на екран)
Фронтальна бесіда
- Що таке вектор?
- Які вектори називаються однаково напрямленими (протилежно напрямленими)?
- Чим характеризується вектор?
- Що таке модуль вектора?
- Який вектор має такі властивості: його початок збігається з його кінцем, напрямок визначити не можна
-
Сформулюйте твердження, зворотне даному: рівні вектори
однаково напрямлені і рівні по абсолютній величині. -
Закінчите речення: від будь-якої точки можна відкласти вектор,
рівний даному .... (вектору, і тільки один).
ІІІ. Тема уроку. Знайомство з новим матеріалом
Лекція
Кожна точка на площині задається двома координатами (х, у). Нехай вектор а починається в крапці А1 (х1, у1) і закінчується в точці А2 (х2, у2).
Координатами вектора а називається число х = х2-х1, у = у2-у1: а (х, у).
Питання. Що можна сказати про координати нульового вектора? (Вони дорівнюють нулю)
Знаючи формулу відстані між двома точками А1(х1;у1) і А2(х2;у2) можна знайти довжину вектора А1А2=√(х1-х2)2+(у1-у2)2 = √х2+у2. Отриманий вираз є абсолютною величиною вектора ![]() (х;у).
(х;у).
Теорема(властивість і ознака координат рівних векторів): Рівні вектори мають рівні відповідні координати.
Доведення:
Нехай А1(х1;у1) і А2(х2;у2) - початок і кінець вектора а.
Вектор ![]() ΄=
΄=![]() отримується паралельним переносом а, то його початком і кінцем будуть відповідно точки А1΄(х1+с;у1+d), А2(х2+с;у2+d).
отримується паралельним переносом а, то його початком і кінцем будуть відповідно точки А1΄(х1+с;у1+d), А2(х2+с;у2+d).
Знайдемо координати: ![]() ´(х2-х1;у2-у1); а´(х2+с-х1-с;у2+d-у1-d)=(х2-х1;у2-у1). Отже,
´(х2-х1;у2-у1); а´(х2+с-х1-с;у2+d-у1-d)=(х2-х1;у2-у1). Отже, ![]() і
і ![]() ´ мають однакові координати.
´ мають однакові координати.
Обернена : якщо у векторів відповідні координати рівні, то вектори рівні .
Доведення .
Нехай А1А2(х1;у1) і А1´А2´(х1´;у1´) мають рівні координати,
де А1´(х1´;у1´), А2´(х2´;у2´).
Із умови теореми х2-х1=х2´-х1´, у2-у1=у2´-у1´.
Звідси, х2´=х2+х1´-х1, у2´=у2+у1´-у1.
Паралельний перенос задається формулами: х´=х+х1´-х1, у´=у+у1´-у1 і переводить точку А1 в точку А1´, а точку А2 - в точку А2´,
тобто вектори ![]() і
і ![]() рівні.
рівні.
Для векторів визначені операції додавання і віднімання.
Сумою векторів ![]() з координатами а1, а2 і b1, b2 називаеться вектор
з координатами а1, а2 і b1, b2 називаеться вектор ![]() з координатами (а1+b1;а2+в2):
з координатами (а1+b1;а2+в2): ![]() (а1;а2)+
(а1;а2)+![]() (b1;b2)=
(b1;b2)= ![]() (а1+b1;а2+b2).
(а1+b1;а2+b2).
Властивості : 1) ![]() +
+![]() =
=![]() +
+![]() ; 2)
; 2) ![]() +(
+(![]() +
+![]() )=(
)=(![]() +
+![]() )+
)+![]() .
.
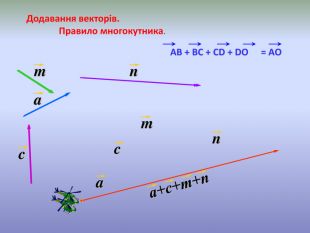
Суму векторів можна побудувати: за правилом «паралелограма» і за правилом "трикутника". (Презентація №1, слайди 16-18 )
-
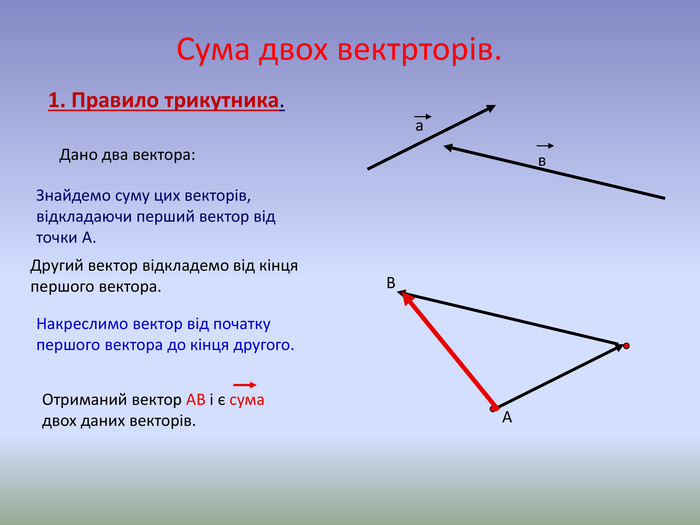
 Правило трикутника А В
Правило трикутника А В
Дано два вектора:
Знайдемо суму цих векторів, відкладаючи перший вектор від точки А.
Другий вектор відкладемо від кінця першого вектора.
Накреслимо вектор від початку першого вектора до кінця другого.
Отриманий вектор АВ і є сума двох даних векторів.
Теорема (про суму векторів)
Які б не були точки А, В, С виконується векторна рівність: ![]() +
+![]() =
=![]() .
.
Доведення .
Нехай А(х1;у1), В(х2;у2), С(х3;у3) - дані точки .
![]()
![]() В
В
![]()
А С
Координати ![]() (х2-х1;у2-у1),
(х2-х1;у2-у1), ![]() (х3-х2;у3-у2),
(х3-х2;у3-у2), ![]() +
+![]() (х2-х1+х3-х2;у2-у1+у3-
(х2-х1+х3-х2;у2-у1+у3-
-у2)=(х3-х1;у3-у1), ![]() (х3-х1;у3-у1).
(х3-х1;у3-у1). ![]() =
=![]() +
+![]() , так як ці вектори мають однакові координати.
, так як ці вектори мають однакові координати.
 З теореми про суму векторів отримуємо спосіб побудови суми векторів за правилом "трикутника". Для застосування цього правила потрібно розташовувати вектори так, щоб кінець першого був початком другого. Тоді сумою цих векторів буде третій вектор, початок якого збігається з початком першого вектора, а кінець з кінцем другого.
З теореми про суму векторів отримуємо спосіб побудови суми векторів за правилом "трикутника". Для застосування цього правила потрібно розташовувати вектори так, щоб кінець першого був початком другого. Тоді сумою цих векторів буде третій вектор, початок якого збігається з початком першого вектора, а кінець з кінцем другого.
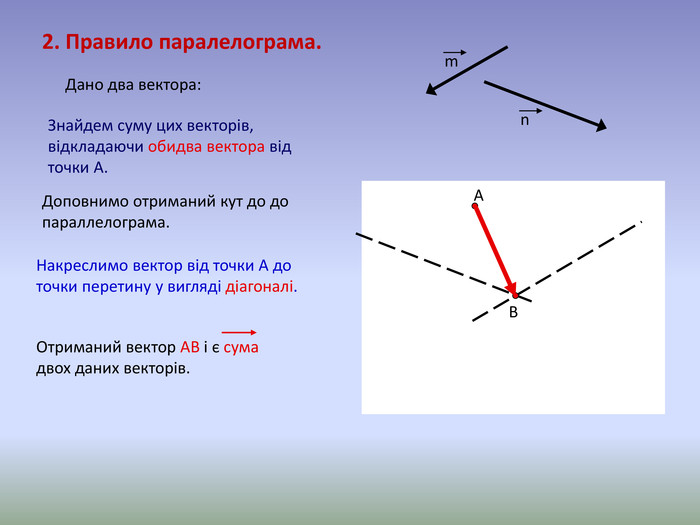
Для векторів із загальним початком їх сума
зображується діагоналлю паралелограма,
побудованого на цих векторах. Це правило «паралелограма».
![]() +
+![]() =
=![]() ,
, ![]() =
=![]() , тоді
, тоді ![]() +
+![]() =
=![]()
Різницею векторів ![]() (а1;а2) і
(а1;а2) і ![]() (b1;b2) називаеться такий вектор
(b1;b2) називаеться такий вектор ![]() , який в сумі з вектором
, який в сумі з вектором ![]() дає вектор
дає вектор ![]() :
: ![]() +
+![]() =
=![]() ; координати вектора
; координати вектора ![]() : с1=а1-b1, с2=а2-b2.
: с1=а1-b1, с2=а2-b2.
V. Формування навичок знаходження координат вектора, абсолютної величини вектора, суми і різниці векторів
Фронтально-колективна робота
Учні, які зрозуміли поданий матеріал, можуть розв’язувати завдання самостійно, консультуючись у вчителя
№1. Вектори ![]() (2;4),
(2;4), ![]() (-1;2) і
(-1;2) і ![]() (с1;с2) відкладені від початку координат. Чому дорівнюють координати їх кінців?
(с1;с2) відкладені від початку координат. Чому дорівнюють координати їх кінців?
Розвязання .
1) Дано вектор ![]() (2;4). Початок вектора - точка О(0;0),
(2;4). Початок вектора - точка О(0;0),
кінець вектора - А(а;b). Тоді 2=а-0, а=2; 4=b-0. b=4.
Отримали А(2;4).
2) В(х;у): -1=х-0, х=-1; 2=у-0, у=2. В(-1;2).
3) С(х1;у1): с1=х1-0, х1=с1; с2=у1-0, с2=у1. С(с1;с2).
№2. ) Абсолютна величина вектора ![]() (5;m) рівна 13,
(5;m) рівна 13,
а вектора ![]() (n;24) рівна 25. Знайти m, n.
(n;24) рівна 25. Знайти m, n.
Розв’язання .
Дано вектор ![]() (5;m). Тоді √25+m² =13, 25+m²=169, m²=144, m1=12, m2= -12.
(5;m). Тоді √25+m² =13, 25+m²=169, m²=144, m1=12, m2= -12.
Дано вектор ![]() (n;24). Тоді √n²+242 = 25, n²+576= 625, n²=49, n1=7, n2= -7.
(n;24). Тоді √n²+242 = 25, n²+576= 625, n²=49, n1=7, n2= -7.
№3. Дано точки А(0;1), В(1;0), С(1;2), D(2;1). Доведіть рівність векторів ![]() і
і ![]() .
.
Доведення .
Знайдемо довжини векторів ![]() і
і ![]() :
: ![]() = √(0-1)2+(1-0)2 =
= √(0-1)2+(1-0)2 = ![]() .
.
Для того щоб вектори ![]() і
і ![]() були рівні між собою, вони повинні суміщатися паралельним переносом,
були рівні між собою, вони повинні суміщатися паралельним переносом,
тобто С(1;2)=А(0+m;1+n) і D(2;1) =В(1+m;0+n).
Перевіримо, чи рівні m і n для точок С і D.
Для точки С: 1=0+m, m=1; 2=1+n, n=1.
Для точки D: 2=1+m, m=1; 1=0+n, n=1.
Значення m і n рівні, отже, вектори ![]() і
і ![]() суміщаються паралельним переносом. Отже,
суміщаються паралельним переносом. Отже, ![]() =
=![]() .
.
№4.Знайдіть вектор ![]() , рівний сумі векторів
, рівний сумі векторів ![]() і
і ![]() і абсолютну величину вектора
і абсолютну величину вектора ![]() , якщо
, якщо ![]() (1;-4),
(1;-4), ![]() (-4;8).
(-4;8).
Розв’язання .
![]() (1:4),
(1:4), ![]() (-4;8),
(-4;8), ![]() =
=![]() +
+![]() ;
; ![]() (1-4;-4+8),
(1-4;-4+8), ![]() (-3;4).
(-3;4). ![]() =√(-3)2+42 =
=√(-3)2+42 = ![]() = 5.
= 5.
№5. Дано ∆АВС. Знайдіть суму векторів : 1) ![]() і
і ![]() ; 2)
; 2) ![]() і
і ![]() .
.
Розв’язання .
![]()
![]() В
В
![]() А С
А С
![]() +
+![]() =
=![]() .
.
![]() В′
В′
![]()
![]() В(А)
В(А)
![]() А
А
С
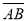 +
+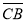 =
=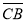 ´,
´, 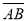 ´=
´=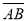 ; (А→В; В→В′)
; (А→В; В→В′)
№6. Знайдіть вектор ![]() =
=![]() -
-![]() і його абсолютну величину,
і його абсолютну величину,
якщо ![]() (1;-4),
(1;-4), ![]() (-4;8).
(-4;8).
VІ. Підсумок уроку
- З якими поняттями познайомилися на уроці?
- В чому особливість операції стеження для векторів?
- Для яких векторів можна виконати додавання по правилу "трикутника", за правилом «паралелограма”?
VІІ. Домашнє завдання
§ 14 пункт 14.3, §15
А- №458, №494(а,б) В- № 459, №496 С- №462, №503(а,б)
Урок №5
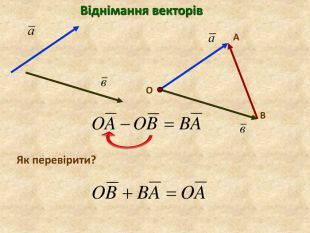
Тема : Віднімання векторів.
Мета уроку: ввести поняття різниці двох векторів, навчити будувати різницю двох даних векторів двома способами; вчити вирішення завдань. Розвивати інтелект учнів, уміння аналізувати, порівнювати. Виховувати позитивне ставлення учнів до навчально-пізнавальної діяльності.
Обладнання: : таблиця «Декартові координати та вектори на площині», креслярські інструменти,ноутбук, проектор.
Тип уроку: комбінований
Хід уроку
І. Організаційний етап.
- Аналіз результатів самостійної роботи.
-
Проаналізувати характерні помилки, допущені в самостійній роботі.
2. Розв’язати на дошці завдання, що викликали труднощі в учнів.
ІІ. Перевірка домашнього завдання
- Перевірка правильності виконання домашнього завдання здійснити за записами, зробленими на дошці до початку уроку.
- Математичний диктант
Дано точки:
Варіант 1 Варіант 2
А(4; 5), В(1; 1) А(2; 3), В(-1; -1)
Запишіть:
а) координати вектора ![]() ;
;
б) координати вектора ![]() +
+ ![]() ;
;
в) довжину вектора ![]() ;
;
г) довжину вектора ![]() ;
;
д) довжину вектора ![]() ;
;
є) довжину вектора ![]() +
+ ![]() .
.
ІII. Сприймання та усвідомлення нового матеріалу
План вивчення теоретичного матеріалу
- Різниця векторів, які задані своїми координатами.
- Побудова вектора — різниці двох векторів.
- Означення протилежних векторів.
- Деякі властивості різниці векторів:
а) ![]() –
– ![]() = 0;
= 0;
б) ![]() –
– ![]() =
= ![]() .
.
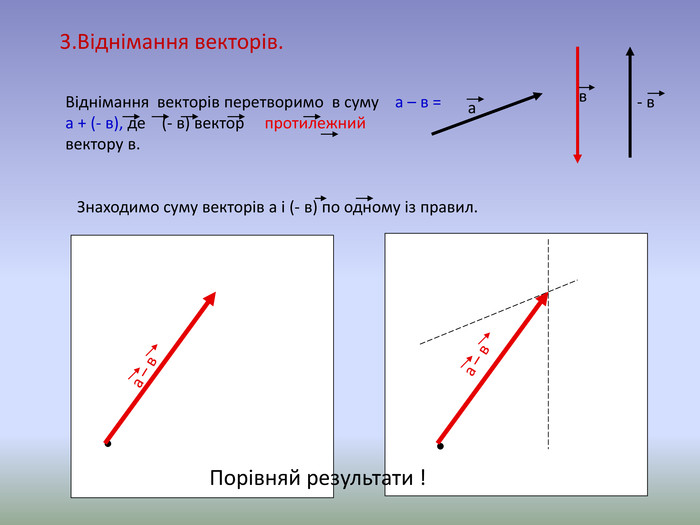
Вивчення нового матеріалу можна провести відповідно до п. 15.2 підручника
1. Нагадати учням означення різниці двох чисел:
а - в = с, то а = с + в,
наприклад, 20 - 14 = 6, то 20 = 6 + 14.
2.Запропонувати учням самим «придумати» означення різниці двох векторів.
Різницею векторів ![]() і
і ![]() називають такий вектор
називають такий вектор ![]() , сума якого з вектором
, сума якого з вектором ![]() дорівнює вектору
дорівнює вектору ![]() .
.
Пишуть: ![]() =
= ![]() –
– ![]() .
.
Якщо координати векторів ![]() і
і ![]() відповідно дорівнюють (a1; a2) і (b1; b2), то координати вектора
відповідно дорівнюють (a1; a2) і (b1; b2), то координати вектора ![]() –
–![]() дорівнюють (a1 – b1; a2 – b2).
дорівнюють (a1 – b1; a2 – b2).
.
Теорема. Для векторів ![]() і
і ![]() із спільним
із спільним
початком ![]() .
.
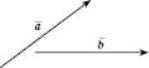
Щоб знайти різницю векторів ![]() і
і ![]() , треба від однієї точки відкласти вектори в
, треба від однієї точки відкласти вектори в ![]() і
і ![]() , що дорівнюють їм (див. рисунок). Тоді вектор, початок якого збігається з кінцем вектора
, що дорівнюють їм (див. рисунок). Тоді вектор, початок якого збігається з кінцем вектора ![]() , а кінець — з кінцем
, а кінець — з кінцем ![]() , буде різницею
, буде різницею ![]() і
і ![]() .
.
Тобто, якщо вектори ![]() і
і ![]() мають спільний початок, вектор
мають спільний початок, вектор ![]() іде з кінця від’ємника в кінець зменшуваного. (Презентація №1, слайди 22,23)
іде з кінця від’ємника в кінець зменшуваного. (Презентація №1, слайди 22,23)
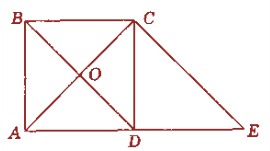 III. Закріплення й осмислення нового матеріалу
III. Закріплення й осмислення нового матеріалу
Розв'язування задач :фронтально-колективна робота (учні, за бажанням можуть працювати самостійно, консультуючись у вчителя)
- На малюнку зображено квадрат ABCD, CE || BD.
- Доведіть, що:
a) ![]() +
+ ![]() =
= ![]() +
+ ![]() ; б) (
; б) (![]() +
+ ![]() ) +
) + ![]() =
= ![]() ;
;
в) (![]() +
+ ![]() ) + (
) + (![]() +
+ ![]() ) =
) = ![]() ; г) (
; г) (![]() +
+ ![]() ) +
) + ![]() =
= ![]() +
+ ![]() ;
;
д) ![]() +
+ ![]() =
= ![]() .
.
-
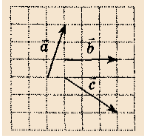 Побудуйте вектор: а)
Побудуйте вектор: а) 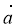 +
+ 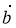 –
– 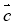 ; б)
; б) 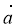 –
– 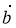 +
+ 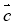 ; в) -
; в) -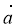 +
+ 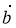 +
+ 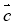 ; г)
; г) 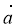 –
– 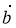 –
– 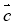 .
.
4. У рівнобедреному трикутнику ABC точка М — середина основи АС.
а) Спростіть: ![]() –
– ![]() +
+ ![]() ;
;
б) знайдіть ![]() , якщо АВ = 5 см, ВМ = 4 см.
, якщо АВ = 5 см, ВМ = 4 см.
-
ABCD — ромб, AD = 20 см, BD = 24 см, О — точка перетину діагоналей. Знайдіть
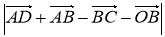 .
.
-
У трапеції ABCD кут А прямий, АС — діагональ,
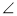 BCA = 45°,
BCA = 45°, 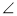 ACD = = 90°, AC = a. Знайдіть
ACD = = 90°, AC = a. Знайдіть  .
.
«Аукціон ідей»:Учні працюють в парах, обираючи завдання по силі. Дерез декілька хвилин учні виставляють на аукціон ідеї щодо розв’язання тієї чи іншої задачі. Кожна ідея оцінюється класом.(Презентація №2 слайди 1-10)
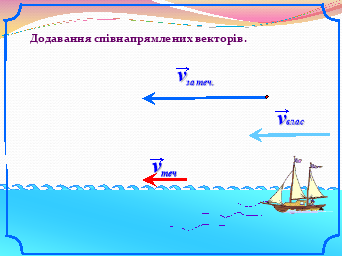
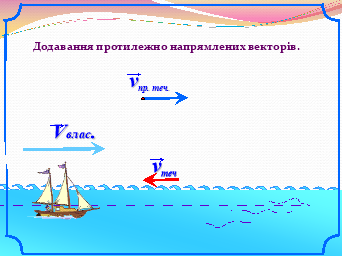
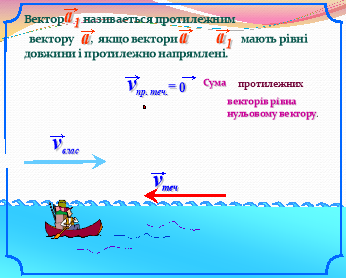
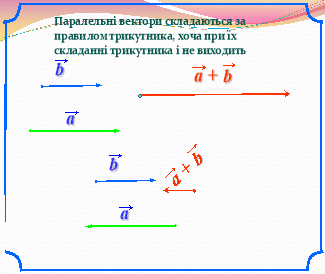
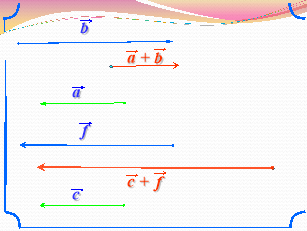
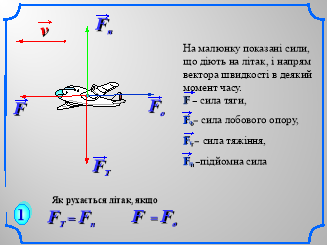
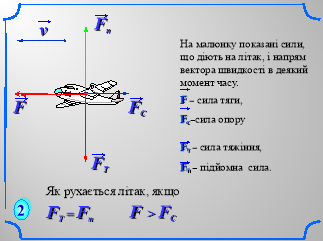
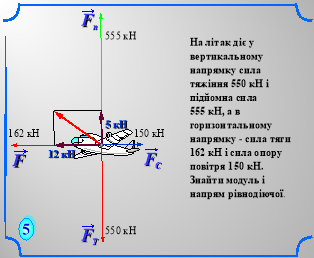
IV. Перевірочна самостійна робота.
Варіант I
Дано прямокутний трикутник АВС з гіпотенузою ВС. Побудуйте вектор![]()
і знайдіть ![]() , якщо
, якщо
AB = 8 см.
Варіант II
Дано прямокутний трикутник АВС з гіпотенузою АВ. Побудуйте ![]()
і знайдіть ![]() ,
,
якщо BС = 9 см.
Варіант III
(Для більш підготовлених учнів)
Дана трапеція ABCD з основами АD і BC. Побудуйте вектор ![]() і знайдіть
і знайдіть ![]() , якщо АD = 12 см, BC = 5 см.
, якщо АD = 12 см, BC = 5 см.
V. Підсумок уроку :
Заповніть пропуски в тексті.
-
Щоб побудувати вектор
 , який дорівнює
, який дорівнює 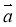 –
– 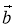 , досить додати вектори
, досить додати вектори 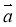 і ...
і ...
-
Щоб побудувати вектор
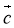 , який дорівнює
, який дорівнює 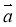 –
– 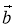 , треба відкласти ці вектори від однієї точки, тоді початок вектора
, треба відкласти ці вектори від однієї точки, тоді початок вектора 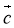 збігається з кінцем вектора ..., а кінець вектора
збігається з кінцем вектора ..., а кінець вектора 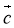 збігається з кінцем вектора ...
збігається з кінцем вектора ...
-
Для будь-яких трьох точок А, В, С справджується рівність
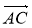 –
– 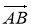 = ... .
= ... .
VІ. Домашнє завдання
Розв'язати задачі.
- Трикутник ABC рівнобедрений, СМ — медіана, проведена з вершини його прямого кута.
а) Спростіть: ![]() –
– ![]() +
+ ![]() ;
;
б) знайдіть ![]() , якщо АВ = 10 см.
, якщо АВ = 10 см.
-
У прямокутнику ABCD AD = 12 см, CD = 5 см, О — точка перетину діагоналей. Знайдіть
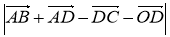 .
.
- Від пристані до протилежного берега річки вийшов катер зі швидкістю 40 км/год. Швидкість течії річки 5 км/год. Позначте на рисунку напрям, у якому має рухатися катер, щоб прийти до найближчої точки протилежного берега річки.
- Вантаж спускається на парашуті зі швидкістю 3 м/с. Вітром його відносить убік зі швидкістю 2 м/с. Під яким кутом до вертикалі буде спускатися вантаж за цих умов?
Урок №9
Тема уроку: Скалярний добуток векторів у координатах і його властивості
Мета уроку: сформулювати і довести теорему про скалярний добуток двох векторів у координатах і її наслідки; ознайомити учнів з властивостями скалярного добутку векторів; показати застосування скалярного добутку векторів при вирішенні задач. Розвивати вміння лаконічно й математично грамотно висловлювати свою думку. Виховувати працьовитість, спостережливість, кмітливість.
Матеріали та обладнання уроку: мультимедіа проектор, слайд-фільм (презентація в PowerPoint), комп'ютерний клас (бажано).
План проведення уроку:
I. Організація учнів.
II. Повідомлення нової теми і постановка мети уроку.
III. Математична розминка:
а) теоретична розминка;
б) математичний тест.
IV. Пояснення нового матеріалу.
V. Закріплення вивченого матеріалу.
VI. Д / з та інструкція до нього.
VII. Підведення підсумків уроку (повідомлення оцінок учням).
Хід уроку
I. Організаційний етап (Презентація№3, Слайд № 1)
На дошці висловлювання про математику:
"Виміряй свої бажання,
зважуй свої думки,
перелічиш свої слова".
Піфагор
Взаємне привітання, з'ясування відсутніх (причини); організація уваги, оголошення теми та мети уроку.
Нагадати, що б зошити з виконаним д / з учні здали в кінці уроку.
II. Постановка мети уроку.
Ми продовжуємо вивчення теми співвідношення між сторонами і кутами трикутника і сьогодні з'ясуємо:
• як обчислюється скалярний добуток двох векторів, знаючи координати цих векторів;
• сформулюємо основні властивості скалярного твори векторів.
А почнемо ми наш урок з теоретичної розминки.
ІІІ. Математична розминка. (Слайд № 2 ,Презентація №3)
1 частина.
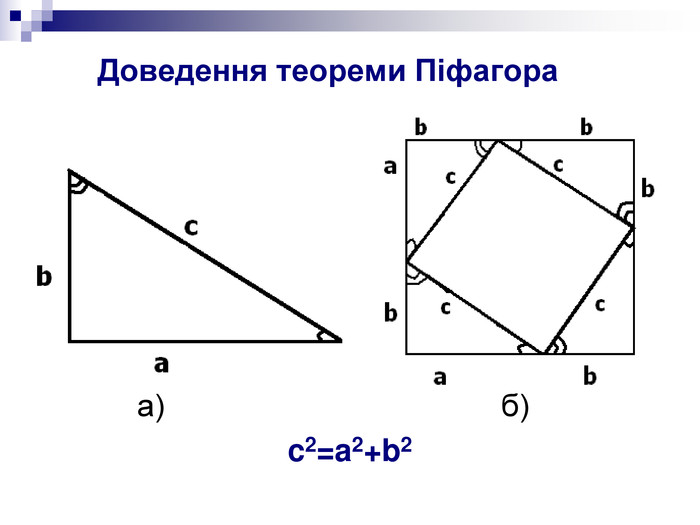
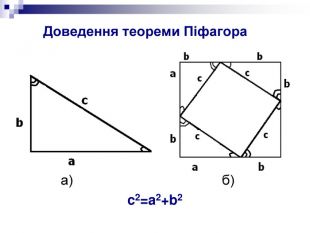
Двоє учнів проводили дослідницьку роботу на доведення теореми Піфагора із застосуванням
1) теореми косинусів ,
2) знаходження довжини вектора.
Поки учні оформляють доведення біля дошки, ми перевіримо ваші знання, проведемо теоретичну розминку (усно).
Теоретична розминка (усно).:
• Сформулюйте теорему синусів (написати формулу на дошці).
• Сформулюйте теорему косинусів (написати формулу на дошці).
• Що значить "розв’язати трикутник"?
• Яке найменше число елементів треба знати, щоб "розв’язати трикутник"?
• Сформулюйте означення скалярного добутку векторів (написати формулу на дошці).
2 частина.
Називаючи правильні відповіді, ми розгадаємо по буквах зашифроване слово.
![]()
Завдання (Презентація№3, Слайд № 3)
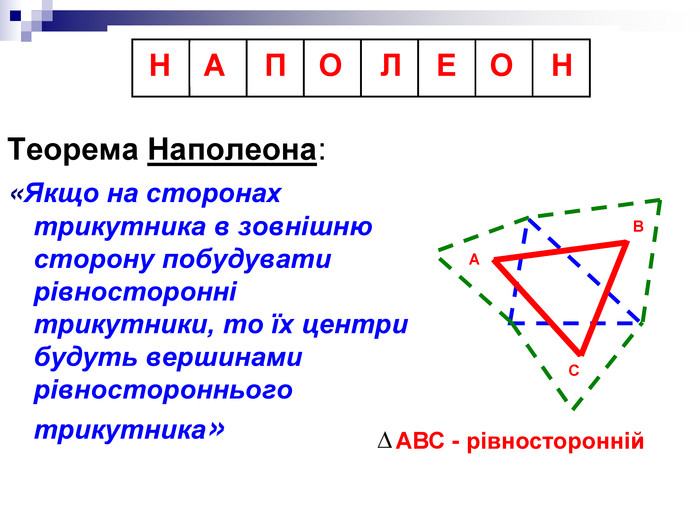
Тут зашифровано ім'я автора цієї красивої теореми:
"Якщо на сторонах трикутника в зовнішню сторону побудувати рівносторонній трикутники, то їх центри будуть вершинами рівностороннього трикутника".
Цей трикутник носить ім'я автора. Це ім'я кожному відомо, але не в математики. Математикою ця людина займався задоволення ради. Він - автор кількох теорем і відомих цікавих геометричних задач. А своє ім'я він прославив на весь світ зовсім з іншого приводу. Отже, давайте спробуємо розгадати ім'я автора цієї теореми (Наполеон Бонапарт).(Презентація№3, Слайд № 4)
Визначте, до якого типу задач "рішення трикутника" можна віднести дану модель малюнка:
(З'являються моделі задач по черзі, варіанти відповідей внизу під певною буквою)
|
Модель 1 |
Модель 2 |
Модель 3 |
Модель 4 |
Модель 5 |
Модель 6 |
п) розв’язування трикутника за трьома сторонами.
л) розв’язування трикутника за двома сторонами і куту, протилежного однієї з них.
о) розв’язування трикутника по стороні і кутах, один з яких лежить проти даної сторони.
н) розв’язування трикутника за двома сторонами і куту між ними.
о) розв’язування трикутника за трьома кутах.
е) розв’язування я трикутника не здійснюється.
а) розв’язування трикутника по стороні і прилеглих кутах.
(Презентація №3, Слайд № 5)
-
Результатом скалярного добутку векторів є ...
а) вектор. о) число. л) градус.
-
Скалярний квадрат координатного вектора
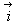 рівний:
рівний:
а) -1. б) 0. в) 1.
(Презентація №3, Слайд № 6)
Після відгадування слова, можна запропонувати учневі (або декільком) за бажанням дома провести дослідницьку роботу з доведення Теореми Наполеона.
Далі учні приводять доведення теорем Піфагора.
Паралельно на екрані Презентація. Слайд № 7 висвічується доведення теореми, яке було застосоване в 8-му класі.
Тест з подальшою взаємоперевіркою
Час відведений на виконання тесту - 5 хвилин
В-1
![]()
![]() 1. Відомо, що
1. Відомо, що ![]() , де і і ј - одиничні вектори. Координати вектора
, де і і ј - одиничні вектори. Координати вектора ![]() рівні:
рівні:
а) ![]() . б)
. б) ![]() . в)
. в) ![]() .
.
![]()
![]()
![]()
![]() 2. Дано вектори а(-1;2) і в(2;4). Координати суми векторів а і в дорівнює:
2. Дано вектори а(-1;2) і в(2;4). Координати суми векторів а і в дорівнює:
а) ![]() . б)
. б) ![]() . в)
. в) ![]() .
.
3. Знайдіть координати вектора ![]() , Якщо
, Якщо ![]() .
.
а) ![]() . б)
. б) ![]() . в)
. в) ![]() .
.
4. Дві сторони трикутника рівні 7 см і 3 см, кут між ними дорівнює 1200. Третя сторона трикутника рівна:
а) ![]() . б)
. б) ![]() . в)
. в) ![]() .
.
![]()
![]() 5. Скалярний добуток координатних векторів і і ј дорівнює:
5. Скалярний добуток координатних векторів і і ј дорівнює:
а) 1; б) -1; в) 0.
В-2
![]()
![]() 1. Відомо, що
1. Відомо, що![]() , де і і ј - одиничні вектори. Координати вектора
, де і і ј - одиничні вектори. Координати вектора ![]() дорівнюють:
дорівнюють:
а) ![]() . б)
. б) ![]() . в)
. в) ![]() .
.
![]()
![]() 2. Дано вектори а(-1;2) і в(2;1). Координати різниці векторів дорівнює:
2. Дано вектори а(-1;2) і в(2;1). Координати різниці векторів дорівнює:
а) ![]() . б)
. б) ![]() . в)
. в) ![]() .
.
3. Знайдіть координати вектора ![]() , якщо
, якщо ![]() .
.
а) ![]() . б)
. б) ![]() . в)
. в) ![]() .
.
4. дві сторони трикутника дорівнюють 3 см і 9 см, кут між ними дорівнює 600. Третя сторона трикутника рівна:
а) ![]() . б)
. б) ![]() . в)
. в) ![]() .
.
![]()
![]() 5. Скалярний добуток двох ненульових векторів а і в дорівнює нулю. Чому дорівнює кут між векторами?
5. Скалярний добуток двох ненульових векторів а і в дорівнює нулю. Чому дорівнює кут між векторами?
а) 1800; б) 900; в) 00.
(зникнення фігур Презентація№3, Слайд № 8).
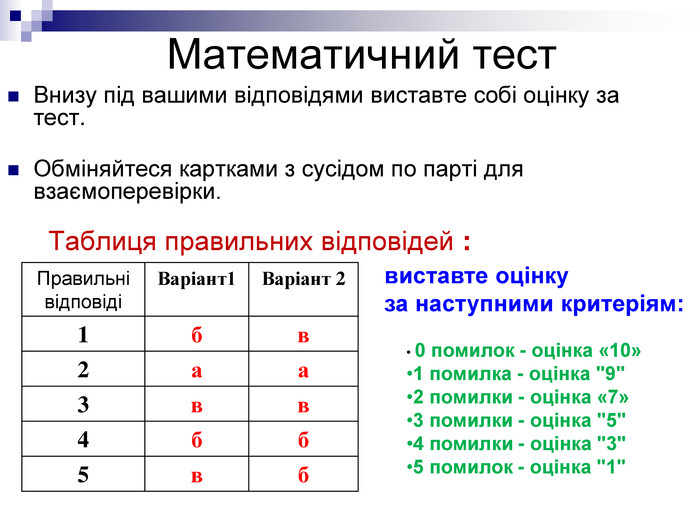
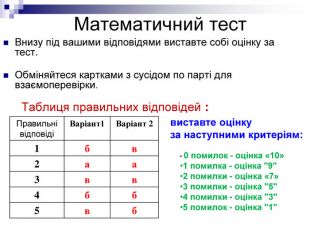
Учні спочатку виставляють собі оцінку, потім обмінюються картками і перевіряють відповіді один в одного за відповідями, заздалегідь підготовленим на екрані у вигляді такої таблиці:(Слайд № 9)
|
Правильні відповіді |
Варіант 1 |
Варіант 2 |
|
1 |
б |
в |
|
2 |
а |
а |
|
3 |
в |
в |
|
4 |
б |
б |
|
5 |
в |
б |
Виставляють оцінку за такими критеріями:
- 0 помилок - оцінка «10»
- 1 помилка - оцінка "9"
- 2 помилки - оцінка «7»
- 3 помилки - оцінка "5"
- 4 помилки - оцінка "3"
- 5 помилок - оцінка "1"
Картка для відповідей математичного тесту:
В-____ Роботу виконав П.І.___________________
|
№ питання |
Відповіді |
Роботу перевіривП.і.______________ |
Підсумкова оцінка (учителя) |
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
Оцінка |
|
|
|
![]()
![]() IV. Пояснення нового матеріалу.
IV. Пояснення нового матеріалу.
Скалярний добуток двох векторів можна обчислити, знаючи координати цих векторів.(Презентація. Слайд № 10)
Теорема: Скалярний добуток векторів а(х1;х2) і в(у1;у2)
![]() выражаєтся формулою
выражаєтся формулою
![]()
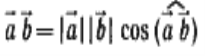 Порівняємо формули :
Порівняємо формули :
Один учень доводить теорему.
Для введення 2 наслідків з теореми можна запропонувати всім учням вирішити два завдання (1 завдання слабким учням, 2 - більш сильним).
Задача 1.
![]()
![]()
![]() Відомо, що ненульові вектори а(х1;х2) і в(у1;у2 )перпендикулярні. Знайдіть
Відомо, що ненульові вектори а(х1;х2) і в(у1;у2 )перпендикулярні. Знайдіть ![]() .
.
Дано:
Знайти: ![]()
![]() Розв’язання:
Розв’язання:![]() і
і
Якщо рівні ліві частини, то і рівні праві. Отже : 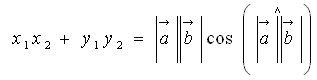
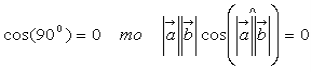
Тоді ![]()
Наслідок 1:Два ненульові вектори тоді і тільки тоді взаємно
перпендикулярні, коли їх скалярний добуток дорівнює нулю,
тобто ![]()
![]()
![]()
![]()
![]() ·
· ![]() = 0 (
= 0 (![]()
![]()
![]() ,
, ![]()
![]()
![]() ).
).
Задача 2. Відомо, що ненульові вектори а(х1;х2) і в(у1;у2 ) і
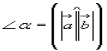 Знайти
Знайти ![]() .
.
Дано:, а(х1;х2) і в(у1;у2 ),
Знайти: ![]()
Розв’язання :
![]() і
і![]()
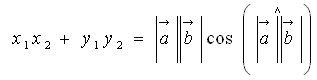 Якщо рівні ліві частини, то і рівні праві.
Якщо рівні ліві частини, то і рівні праві.
Отже:
Із формули слідує:
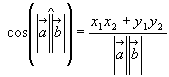 або
або 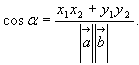
Так як 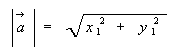 і
і 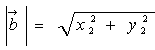 , то
, то
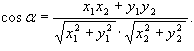
Наслідок 2: Косинус кута між ненульовим векторами ![]() та
та ![]() виражається формулою
виражається формулою 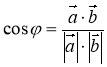
|
|
Закон |
дії з числами (властивості) a , b і с – довільні числа |
Дії над векторами (властивості)
|
|
1 |
переставний |
|
|
|
2 |
розподільний |
|
|
|
3 |
сполучний |
|
|
|
4 |
|
|
при |
Вирішивши завдання, ми разом сформулювали наслідки 1 і 2
(Презентація №3, Слайд №11 )
Читати самостійно наслідки на сторінці 166.
Далі вводимо властивості скалярного добутку векторів через порівняння дій над числами: (Презентація №3, Слайд №12 )
Учні перевіряють свої записи, зроблені на попередньому уроці.
![]() Зауваження: Розподільний закон має місце для будь-якого числа доданків. Наприклад,.
Зауваження: Розподільний закон має місце для будь-якого числа доданків. Наприклад,.
V. Закріплення вивченого матеріалу.( Презентація №3, Слайд № 13)
Колективне розв’язання з коментуванням
 Один з учнів, вирішуючи задачу біля дошки, коментує рішення вголос, інші уважно його слухають, роблячи при цьому записи в зошиті, і вносять виправлення, якщо учень припустився помилки.
Один з учнів, вирішуючи задачу біля дошки, коментує рішення вголос, інші уважно його слухають, роблячи при цьому записи в зошиті, і вносять виправлення, якщо учень припустився помилки.
-
Сторона рівностороннього трикутника ABC дорівнює 13. Знайдіть скалярний добуток
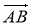 ·
·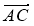
Розв'язання
Оскільки |![]() | = |
| = |![]() | = 13,
| = 13, ![]() A = 60°,
A = 60°,
то ![]() ·
·![]() = |
= |![]() |·|
|·|![]() |cos
|cos![]() A = 13 · 13 cos60°=
A = 13 · 13 cos60°=
= 169 · ![]() = 84,5. Відповідь. 84,5.
= 84,5. Відповідь. 84,5.
-
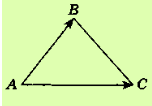 Задано вектори
Задано вектори 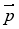 =
= 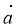 – 4
– 4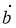 ,
, 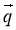 = 3
= 3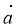 + 2
+ 2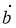 , які взаємно перпендикулярні. Вектори
, які взаємно перпендикулярні. Вектори 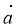 і
і 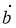 — одиничні вектори. Знайдіть кут між векторами
— одиничні вектори. Знайдіть кут між векторами 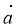 і
і 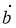 (в градусах).
(в градусах).
Розв'язання
Оскільки |![]() | = 1 і
| = 1 і ![]() ·
· ![]() = 0, то маємо
= 0, то маємо ![]() ·
·![]() = (
= (![]() – 4
– 4![]() )(3
)(3![]() + 2
+ 2![]() ) =
) =
= 3![]() 2 + 2
2 + 2![]()
![]() – 12
– 12![]()
![]() – 8b2 = 3 · |
– 8b2 = 3 · |![]() |2 – 10|
|2 – 10|![]() ||
||![]() | соsφ – 8|
| соsφ – 8|![]() |2 =
|2 =
= 3 - 10cosφ – 8 = - 5 – 10cosφ, тоді – 5 – 10cosφ = 0, соsφ = -![]() , φ = 120°.
, φ = 120°.
Відповідь. 120°.
«Геометрія є наймогутнішим засобом для розвитку
наших розумових здібностей і дає нам
можливість правильно мислити і міркувати »
Галілео Галілей
Самостійне розв’язування вправ: (№535, №547,№ 536, №537)
-
Знайдіть кут між векторами
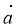 (1; 2) і
(1; 2) і 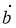
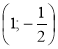 .
.
-
Дано вершини трикутника ABC: А
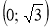 , В
, В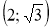 , С
, С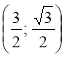 . Знайдіть його кути.
. Знайдіть його кути.
-
Доведіть, що вектори
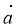 (т; п) і
(т; п) і 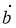 (-n; m) перпендикулярні або дорівнюють нулю.
(-n; m) перпендикулярні або дорівнюють нулю.
-
Дано вектори
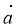 (3; 4) і
(3; 4) і 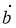 (m; 2). При якому значенні т вони перпендикулярні?
(m; 2). При якому значенні т вони перпендикулярні?
V І. Підсумок уроку
- З якою дією над векторами ми познайомилися на уроці?
- Що спільного між скалярним добутком векторів і натуральними числами? (Властивості)
- Як знайти скалярний добуток векторів, якщо задані їх координати?
- За якої умови можна говорити про перпендикулярність векторів?
VІІ. Домашнє завдання
Завдання для 1 групи (сильнішої- С).
№ 1. Дано: ![]() =
= ![]() +
+ ![]() + √З
+ √З ![]() ,
, ![]() =
= ![]() - √З
- √З ![]() ;
; ![]() ,
, ![]() - одиничні вектори.
- одиничні вектори.
Знайти ![]()
![]() .
.
№ 2. Довести, що сума квадратів діагоналей паралелограма дорівнює сумі квадратів його сторін.
№ 3. Довести, що діагоналі ромба перпендикулярні.
Завдання для 2 групи (слабшої-В).
№ 1. Задача №534
Знайти: І варіант: а), II варіант: в).
№2. Дано: ![]() (0; 1),
(0; 1), ![]() (2;-2).
(2;-2).
Знайти: І варіант: | 2![]() + З
+ З![]() |, II варіант: | -2
|, II варіант: | -2![]() - З
- З![]() |.
|.
№ 3. І варіант.
Дано: ![]() (2п; 3),
(2п; 3), ![]() (6; n) - колінеарні. Знайти: n.
(6; n) - колінеарні. Знайти: n.
II варіант.
Дано: ![]() (т; 1),
(т; 1), ![]() (2; 16) - перпендикулярні. Знайти: т.
(2; 16) - перпендикулярні. Знайти: т.
Урок №8
Тема уроку: Скалярний добуток векторів
Мета уроку: вивчити новий матеріал; реалізувати сформовану в учнів навчально-пізнавальну компетенцію;розвивати вміння працювати самостійно а також самостійно здобувати знання.
Тип уроку: урок самостійного вивчення нового матеріалу
Хід уроку
І. Організаційний етап
Пам'ять – це мідна дошка,
вкрита буквами, які час
непомітно згладжує, якщо
іноді їх не поновлювати різцем.
Д. Локк
1. Перевірка домашнього завдання
Запитання до класу (опитування)
- Які вектори називаються колінеарними?
- Сформулюйте ознаку колінеарності векторів.
- Сформулюйте властивість координат колінеарних векторів
- Дайте означення рівних векторів.
- Як визначити координати вектора.
- Дайте означення суми двох веторів.
- Дайте означення добутку вектора на число.
-
 Як побудувати вектор ка ?
Як побудувати вектор ка ?
Два учні розв’язують Д/З біля дошки
ІІ. Актуалізація опорних знань
Самостійна робота(2 учня працюють біля дошки )
№1. Знайти координати вектора ![]() (а1;а2), якщо задані координати його початку (х1;у1) і кінця(х2;у2).
(а1;а2), якщо задані координати його початку (х1;у1) і кінця(х2;у2).
Розв’язання .
а1=х1-х2, а2=у2-у1.
№2. Знайти абсолютну величину вектора ![]() із №1.
із №1.
Розв’язання .
а2=а12+а22.
ІІІ. Тема уроку
Складання конспекту матеріалу - метод «Відповіді на питання»
Обгрунтування доцільності вибору форми уроку.
На даному уроці учні застосовують один з методів складання конспекту матеріалу - метод «Відповіді на питання». Текст, наведений в підручнику по темі «Скалярний добуток векторів», містить, в основному, головний і важливий матеріал і практично не містить другорядний і вступний матеріал. В учнів може виникнути «спокуса» переписати весь текст повністю. А це вже не конспект! Тому учні, як правило, не можуть бути впевнені у правильності складання конспекту такого тексту - адже нелегко з головного вибрати головне. Заздалегідь складений учителем план показує учням, що навіть в такому непростому, з точки зору конспектуванні, тексту можна (і потрібно) вибрати основне.
Зауваження. 1) Наведений нижче план самостійного вивчення нового матеріалу складено в точній відповідності з § 16, пункт 2 навчального посібника А.П.Єршова та ін. «Геометрія 9».
2) Частина роботи, яку не встигнуть виконати на уроці, учні виконують вдома.
3) На наступному уроці проводиться повторне пояснення матеріалу вчителем, учні самостійно та під керівництвом вчителя доводять теореми і властивості.
Самостійне опрацювання матеріалу
Людина перестає читати –
перестає мислити
Дібро
Роздатковий матеріал
Скалярний добуток векторів
План самостійного вивчення матеріалу
-
Прочитайте текст підручника (§ 16, пункт 2 навчального посібника А.П.Єршова та ін. «Геометрія 9»).
2. Письмово дайте відповідь на наступні питання.- Як позначається кут між двома векторами?
- Як його побудувати (покажіть на прикладах)?
![]() .
. ![]()
3)Які вектори називаються перпендикулярними?
4) Що називається скалярним добутком двох векторів? Як він позначається? (Дайте словесне визначення поняття та визначення у вигляді формули).
5) В чому полягає необхідна і достатня умова перпендикулярності двох ненульових векторів? (Дайте словесну формулювання теореми і формулювання у вигляді формули).
6) Як залежить знак скалярного добутку двох ненульових векторів від виду кута між ними?
7) Що називається скалярним квадратом вектора, як він позначається? (Дайте словесне визначення поняття та визначення у вигляді формули).
8) Запишіть властивості скалярного множення векторів.
3. Розв’язати завдання: № 532 (а, б), № 536 , №534(в)
4. Завдання на додаткову оцінку.
Завдання 1. Довести необхідну і достатню умову перпендикулярності двох ненульових векторів.
Завдання 2. Довести сполучну властивість скалярного множення векторів.
Завдання 3. Довести розподільну властивість скалярного множення векторів.
ІV. Підсумок уроку
- Чи зрозуміли ви новий матеріал?
- Відповіді на які запитання ви знайшли найшвидше?
- На які питання ви не змогли дати відповіді?
- Які нові терміни вам не зрозумілі?
- Чи важко було самостійно опрацьовувати новий матеріал?
- Дайте означення скалярного добутку векторів та сформулюйте властивості скалярного добутку векторів.
- Сформулюйте властивість і ознаку перпендикулярних векторів.
V. Домашнє завдання
1. Закінчити роботу над конспектом (§ 16, пункт 2 навчального посібника А.П.Єршова та ін. «Геометрія 9»).
2. Розв’язати задачі (на окремих аркушах і здати на перевірку)
Група А
- Дано вершини трикутника A(1; 1), B(4; 1), С(4; 5). Знайдіть косинуси кутів цього трикутника.
-
Дано вектори
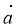 (3; 4) і
(3; 4) і 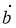 (m; 2). При якому значенні т вони перпендикулярні?
(m; 2). При якому значенні т вони перпендикулярні?
Група В
-
Дано вектори
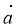 (1; 0) і
(1; 0) і 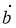 (1; 1). Знайдіть таке число х, щоб вектор
(1; 1). Знайдіть таке число х, щоб вектор 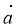 + x
+ x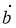 був перпендикулярний до вектора
був перпендикулярний до вектора 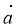 .
.
-
Дано вектори
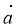 (3; 4) і
(3; 4) і 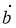 (m; 2). При якому значенні т вони перпендикулярні?
(m; 2). При якому значенні т вони перпендикулярні?
Група С
-
Доведіть, що коли
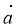 і
і 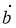 — одиничні неколінеарні вектори, то вектори
— одиничні неколінеарні вектори, то вектори 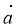 +
+ 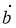 і
і 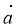 –
– 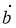 відмінні від нуля й перпендикулярні.
відмінні від нуля й перпендикулярні.
-
Дано вектори
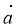 і
і 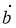 . Знайдіть абсолютну величину вектора
. Знайдіть абсолютну величину вектора 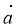 +
+ 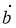 , якщо |
, якщо |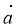 | = |
| = | | = 1, а кут між векторами
| = 1, а кут між векторами  і
і  дорівнює 60°.
дорівнює 60°.
- Дослідницька робота
Доведення теореми Піфагора за курс 8 класу(за бажанням)
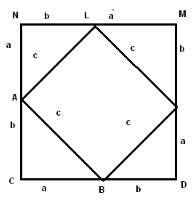 Побудуємо квадрат CDMN з стороною a+b
Побудуємо квадрат CDMN з стороною a+b
Тоді ΔАСВ = ΔBDK = ΔKLM = ΔLNA ( за двома катетами ) , звідки
AB = BK = KL = LA = c.
Отже, чотирикутник ABKL – ромб.
Оскільки ![]() АВК = 90°, то ABKL – квадрат. Маємо:
АВК = 90°, то ABKL – квадрат. Маємо:
![]()
Порівнюючи останні рівності, дістанемо:
![]()
Урок №10
Тема уроку: Скалярний добуток векторів . визначення кута між векторами.
Мета уроку:
- Закріпити знання формули для обчислення кута між двома векторами;
- Продовжувати формувати вміння і навички застосування векторів до вирішення завдань;
- Продовжувати формувати інтерес до математики за допомогою вирішення завдань;
- Виховувати усвідомлене ставлення до процесу навчання, прищеплювати почуття відповідальності за якість знань, здійснювати самоконтроль за процесом рішення та оформлення вправ.
Обладнання :
- Таблиця "Вектори на площині і в просторі";
- Картки-завдання для індивідуального опитування;
- Картки-завдання для перевірочної роботи;.
Хід уроку
І Організаційний етап.
- Перевірка Д/З
- Перевірка виконання письмових завдань здійснюється на перерві перед уроком. Вчитель вибірково перевіряє зошити різних варіантів, учні в свою чергу самостійно звіряються із перевіреними варіантами.
- При потребі на початку уроку робиться аналіз виконання Д/З, активізується увага учнів на допущених помилках.
- Індивідуальний опитування за картками.
Карточка 1.
1. Написати властивості складання двох векторів.
2. При якому значенні m вектори ![]() і
і ![]() будуть колінеарні?
будуть колінеарні?
Карточка 2.
1. що називають добутком вектора на число?
2. чи спів напрямлені вектори ![]() і
і ![]() ?
?
Карточка 3.
1. Сформулювати визначення скалярного добутку двох векторів.
2. При якому значенні к довжини векторів ![]() і
і ![]() будуть рівні?
будуть рівні?
Карточка 4.
1. Записати формули для обчислення координат вектора і довжини вектора?
2 Колінеарні вектори ![]() і
і ![]() ?
?
-
Питання для фронтального опитування:
1. Які дії можна виконувати над векторами, заданими своїми координатами?
2. Які вектори називаються колінеарними?
3. Умова колінеарності двох ненульових векторів?
4. Визначення кута між векторами?
5. Визначення скалярного добутку двох ненульових векторів?
6. Необхідна і достатня умова перпендикулярності двох векторів?
7. У чому полягає фізичний зміст скалярного добутку двох векторів?
8. Записати формули для обчислення скалярного добутку двох векторів через їх координати на площині і в просторі.
9. Записати формули для обчислення довжини вектора на площині і в просторі.
ІІ. Мотивація пізнавальної діяльності учнів.
Сьогодні на занятті ви навчитеся обчислювати кут між векторами, застосовувати отримані знання для вирішення завдань механіки і фізики. Так, при вивченні теми "Знаходження рівнодійної двох сил" застосовується формула обчислення кута між двома векторами.
Пропоную вам розв’язати одну із запропонованих задач, щоб перевірити на скільки добре ви запам’ятали формулу для знаходження кута між векторами.
Задача 1: Знайти кут мвж векторами: ![]() = (1; -2),
= (1; -2), ![]() = (-3; 1).
= (-3; 1).
Задача 2: Знайти кут між векторами ![]() і
і ![]() , якщо А (1; 6), В (1; 0), С (-2; 3).
, якщо А (1; 6), В (1; 0), С (-2; 3).
Розв’язання №1:
cos ![]() =
= 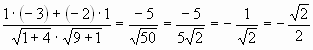
![]() = arccos
= arccos 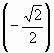 = 135°
= 135°
Розв’язання №2:
![]() = (0; -6)
= (0; -6) ![]() = (-3; 3)
= (-3; 3)
cos ![]() =
= ![]() =
= ![]() = –
= – ![]() ,
, ![]() = 135°
= 135°
IІІ. Застосування знань при вирішенні типових завдань.
ЗАВДАННЯ АНАЛІТИЧНОГО ХАРАКТЕРУ.
(учні обирають собі завдання за рівнем складності)
Задача 1. (8 балів)
Визначити кут між векторами ![]() і
і ![]() , якщо А (1; -3), В (-1; 0), С (2; -4), D (1; 1).
, якщо А (1; -3), В (-1; 0), С (2; -4), D (1; 1).
Задача 2. (10 балів)
Знайти скалярний добуток векторів ![]()
![]() ,
,
якщо ![]() ,
, ![]() = 30°.
= 30°.
Задача 3.(6 балів)
При яких значеннях ![]() довжини векторів
довжини векторів ![]() = (2m; 3),
= (2m; 3), ![]() = (-6; m) будуть рівні?
= (-6; m) будуть рівні?
Задача 4: (9 балів)
Трикутник АВС задано координатами вершин А(1; ![]() ), В(0; 0), С
), В(0; 0), С![]() . Знайдіть кут В трикутника.
. Знайдіть кут В трикутника.
ЗАДАЧІ ПРИКЛАДНОГО ХАРАКТЕРУ
Фронтально-колективна робота. (у розв’язанні задач беруть участь усі учні, вони пропонують варіанти розв'язання, перевіряють, обґрунтовують, розвивають найбільш вдалі, відкидають неправильні. Вчитель при цьому керує колективним пошуком рішень, спрямовує пізнавальну активність учнів.)
Успіх завжди результат індивідуальних зусиль,
але ви обдурюєте себе, якщо вважаєте, що можете
досягти успіху без співпраці з іншими людьми.
Наполеон Хілл
Задача 1.
Знайти рівнодіючу двох сил ![]() 1 і
1 і ![]() 2, якщо
2, якщо ![]() =
= ![]() 5H;
5H; ![]() = 7H,
= 7H,
кут між ними ![]() = 60°.
= 60°.
Розв’язання :
![]()
![]()
![]()
![]() ° +
° + ![]() .
.
![]()
Задача 2.
Обчислити роботу, яку виконує сила ![]() = (6; 2), якщо її точка прикладання, рухаючись прямолінійно, переміщається з положення А (-1; 3),
= (6; 2), якщо її точка прикладання, рухаючись прямолінійно, переміщається з положення А (-1; 3),
в положення В (3; 4).
Розв’язання:
![]()
![]()
![]()
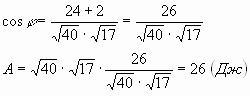
Задача 3.
Нехай ![]() – швидкість матеріальнї точки,
– швидкість матеріальнї точки, ![]() – сила,що діє на неї. Чому дорівнює потужність, що розвивається силою
– сила,що діє на неї. Чому дорівнює потужність, що розвивається силою ![]() , якщо
, якщо ![]() = 5H,
= 5H, ![]() = 3,5 м/с;
= 3,5 м/с; ![]()
![]() = 45°
= 45°
Розв’язання:
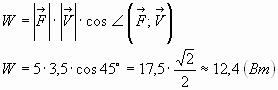
Задача 4.
Вектори ![]() і
і ![]() взаємно
взаємно ![]() . Який кут утворюють вектори
. Який кут утворюють вектори ![]() і
і ![]() , якщо
, якщо ![]() ?
?
ІV. Самостійне застосування знань, умінь і навичок.
Перевірочна робота з вибірковою системою відповідей.
Варіант 1.
-
При якому значенні
 вектори
вектори 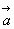 = (
= ( 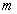 + 1; 1) и
+ 1; 1) и 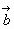 = ( 2; 3
= ( 2; 3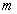 ) будуть перпендикулярні?
) будуть перпендикулярні?
а) -2;
б) 2
в)-2/3;
г) вірної відповіді немає.
-
Знайти довжину вектора
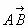 , якщо А (4; 0), В ( 2; -1):
, якщо А (4; 0), В ( 2; -1):
а)√5;
б) ![]()
в) ![]()
г)вірної відповіді немає.
3. Дано вектор ![]() (– 6; 1) і
(– 6; 1) і ![]() (5; – 3). Знайдіть
(5; – 3). Знайдіть ![]() +
+ ![]() .
.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
Варіант 2.
1. При якому значенні ![]() вектори
вектори ![]() ( 6;
( 6; ![]() ) і
) і ![]() (-3/4; 3) будуть колінеарні?
(-3/4; 3) будуть колінеарні?
а) -24;
б) 24;
в) 6
г) вірної відповіді немає.
2. Знайти роботу А, якщо ![]() = 3H;
= 3H; ![]() = 4м,
= 4м, ![]() = 30°
= 30°
а) 6;
б) ![]() ;
;
в) -6;
г)вірної відповіді немає.
3. Скалярний квадрат вектора ![]() дорівнює 9. Знайдіть абсолютну величину вектора
дорівнює 9. Знайдіть абсолютну величину вектора ![]() .
.
а) 3;
б)9;
в) -3;
г)вірної відповіді немає.
Варіант 3.
1. Знайти ![]() если; а(2;0), в(0; -2) кут між векторами 60°
если; а(2;0), в(0; -2) кут між векторами 60°
а) 8;
б) 9;
в) 17;
г)вірної відповіді немає
2. Дано вектори ![]() (х; –4) і
(х; –4) і ![]() (2; 3). Знайдіть значення х, якщо
(2; 3). Знайдіть значення х, якщо ![]()
![]()
![]() .
.
а) -6;
б) 6;
в) ![]() ;
;
г)вірної відповіді немає.
3. Знайти абсолютну величину рівнодійної сил F1 і F2
якщо | F1 | = 3H, a | F2 | = 4H.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() F1
F1
Варіант 3 F2 Варіант 4
Варіант 4.
1. При якому значенні ![]() вектори
вектори ![]() ( m-1;
( m-1; ![]() ) і
) і ![]() (4; 1-m) будуть перпендикулярні?
(4; 1-m) будуть перпендикулярні?
а) -3; -2;
б) 4;
в) 1; 4;
г) -3.
2. Обчислити скалярний добуток векторів ![]()
![]() , якщо а(2;0), в(0; -2), кут між векторами 60°
, якщо а(2;0), в(0; -2), кут між векторами 60°
а) 23;
б) 20;
в) 25;
г) 10.
3. Знайти абсолютну величину рівнодійної сил F1 і F2
якщо | F1 | = 3H, a | F2 | = 4H. (див мал)
V . Підведення підсумків заняття.
Учні повторюють поняття і теореми, які були використані в ході уроку.
VII. Домашнє завдання:
§16 №533 №548, №551
Урок № 6
Тема. Множення вектора на число.
Мета: формування навичок множення вектора на число, додавання і віднімання векторів, сприяти розвитку спостережливості, мислення та мови учнів, виховання самостійності, дисциплінованості.
Обладнання: опорний конспект
Тип уроку: комбінований урок.
Хід уроку.
 І. Організація дітей до роботи на уроці
І. Організація дітей до роботи на уроці
I. Усна робота.
За заздалегідь заготовленим кресленнях на дошці усно вирішити завдання:
1. На малюнку 1 ABCD - паралелограм, O - точка перетину діагоналей. Виразіть через вектори ![]() і
і ![]() вектори:
вектори:
а) ![]() Мал.1
Мал.1
б) ![]() де М – точка на стороні BC, така, що МВ : MC = 3 : 2;
де М – точка на стороні BC, така, що МВ : MC = 3 : 2;
в) ![]() де K – точка на стороні AD, така, що АK : KD = 1 : 3;
де K – точка на стороні AD, така, що АK : KD = 1 : 3;
 г)
г) ![]() де N – точка на діагоналі AC, така, що ON = NC.
де N – точка на діагоналі AC, така, що ON = NC.
2. На малюнку 2 ABCD – трапеція, О – точка перетину діагоналей, ВС || AD, AD = 2BC. Виразіть через вектори ![]() і
і ![]() вектори:
вектори:
а) ![]() б)
б) ![]() Мал. 2
Мал. 2
ПеревіркаД/З: біля дошки 4 учня пояснюють розв’язання задач.
-
 Трикутник ABC рівнобедрений, СМ — медіана, проведена з вершини його прямого кута.
Трикутник ABC рівнобедрений, СМ — медіана, проведена з вершини його прямого кута.

![]()
![]()

![]() а) Спростіть:
а) Спростіть: ![]() –
– ![]() +
+ ![]() =МС
=МС
![]() б) знайдіть
б) знайдіть ![]() , якщо АВ = 10 см.
, якщо АВ = 10 см.
![]()
![]()
![]()
![]() =5см
=5см
- У прямокутнику ABCD AD = 12 см, CD = 5 см, О — точка перетину
діагоналей.
Знайдіть ![]() .
.
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =ІАС-СОІ= ІАОІ,
=ІАС-СОІ= ІАОІ,
За т. Піфагора:144+25=169, ІАО І=13см.
![]()
![]()
![]()
- Від пристані до протилежного берега річки вийшов катер зі швидкістю 40 км/год. Швидкість течії річки 5 км/год. Позначте на рисунку напрям, у якому має рухатися катер, щоб прийти до найближчої точки протилежного берега річки.

![]()
![]()
40км/год 5км/год
45км/год
- Вантаж спускається на парашуті зі швидкістю 3 м/с. Вітром його відносить убік зі швидкістю 2 м/с. Під яким кутом до вертикалі буде спускатися вантаж за цих умов?
2м/с
3м/с соsα = 3/13
ІІ. Повідомлення теми і цілей уроку
Сьогодні ми познайомимося ще з однією математичної операцією, характерною для векторів, дізнаємося, в чому полягає геометричний сенс множення вектора на число. З метою закріплення будемо вирішувати завдання на додавання, віднімання векторів. В кінці уроку напишемо невелику самостійну роботу на вивчений матеріал по векторах.
3. Фронтальна бесіда
Питання:
1. Чому має місце поняття координат вектора?
2. Чому дорівнює абсолютна величина вектора із заданими координатами?
3. Які умови необхідні для рівності векторів?
4. Що називається сумою векторів?
5. Що називається різницею векторів?
6. Сформулюйте правило "трикутника" і правило "паралелограма"
для додавання векторів.
7. Які властивості додавання векторів ви знаєте?
ІІІ. Сприйняття і осмислення нового матеріалу : лекція
Приклад, що підводить до визначення твору вектора на число:
Автомобіль рухається прямолінійно зі швидкістю![]() . Його обганяє другий автомобіль, що рухається зі швидкістю, удвічі більшою. Назустріч їм рухається третій автомобіль, у якого величина швидкості така ж, як у другого автомобіля. Як визначити швидкості другого і третього автомобілів через швидкість
. Його обганяє другий автомобіль, що рухається зі швидкістю, удвічі більшою. Назустріч їм рухається третій автомобіль, у якого величина швидкості така ж, як у другого автомобіля. Як визначити швидкості другого і третього автомобілів через швидкість![]() першого автомобіля і як зобразити за допомогою векторів ці швидкості?
першого автомобіля і як зобразити за допомогою векторів ці швидкості?
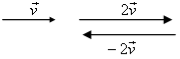
Відповідь дає малюнок. Природно вважати, що швидкість другого автомобіля дорівнює 2![]() (добутку швидкості першого автомобіля на число 2), а швидкості третього автомобіля дорівнює -2
(добутку швидкості першого автомобіля на число 2), а швидкості третього автомобіля дорівнює -2![]() (добутку швидкості на число 2).
(добутку швидкості на число 2).
Означення: Добутком вектора ![]() (х1;х2) називается вектор (λх1;λх2), тобто λ(х1;х2)=(λх1;λх2).
(х1;х2) називается вектор (λх1;λх2), тобто λ(х1;х2)=(λх1;λх2).
Наслідки:
1) для любого вектора а і чисел λ, μ (λ + μ) ![]() = λ
= λ![]() + μ
+ μ![]() ;
;
![]() 2) для любих двох векторів
2) для любих двох векторів ![]() і в і числа λ: λ(
і в і числа λ: λ(![]() +
+![]() ) = λ
) = λ![]() + λ
+ λ![]() .
.
Теорема . Абсолютна величина вектора λ![]() рівна
рівна ![]()
![]() . Напрямок вектора λ
. Напрямок вектора λ![]() при а≠0 співпадає з напрямком вектора
при а≠0 співпадає з напрямком вектора ![]() , якщо λ>0, і протилежний напрямку вектора
, якщо λ>0, і протилежний напрямку вектора ![]() , якщо λ<0.
, якщо λ<0.
Доведення.
1. Побудуємо вектори ОА = ![]() і ОВ = λ
і ОВ = λ![]() ( де О - початок координат). Нехай
( де О - початок координат). Нехай ![]() (а1;а2). Тоді А(а1;а2), В(λа1;λа2).
(а1;а2). Тоді А(а1;а2), В(λа1;λа2).
2.Рівняння прямої ОА має вид: αх+βу=0. Так як рівнянню задовольняють координати точки А(а1;а2), то йому задовольняють координати точки В(λа1;λа2).Отже, точка В лежить на прямій ОА.
3. Координати любої точки С(с1;с2), що лежить на півпрямій ОА, мають ті ж знаки, що і координати точки А(а1;а2), а координати любої точки, що лежить на доповненій півпрямій до ОА, мають протилежні знаки.
4. Якщо λ>0, то точка В належить ОА. Отже, векторі ![]() і λ
і λ![]() однаково напрямлені. Якщо λ<0, то точка В належить додатковій пів прямій до ОА. Звідси слідує, вектори
однаково напрямлені. Якщо λ<0, то точка В належить додатковій пів прямій до ОА. Звідси слідує, вектори ![]() і λ
і λ![]() протилежно напрямлені.
протилежно напрямлені.
5.Знайдемо абсолютну величину вектора λ![]() :
:
λ = √(λа1)2+(λа2)2= =![]() √а12+а22=
√а12+а22=![]()
![]() .
.
Питання. У чому полягає геометричний зміст операції множення вектора на число? (Розтягування чи стиснення вихідного вектора вздовж півпрямої, яка містить цей вектор)
IV. Формування навичок застосування теореми про множення вектора на число. (Презентація №2 , слайди 11,12)

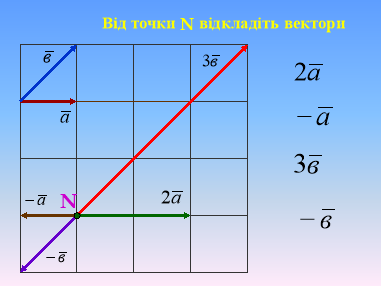 №1. Дано точки А(х1;у1) і В(х2;у2). Доведіть, що вектори
№1. Дано точки А(х1;у1) і В(х2;у2). Доведіть, що вектори ![]() і
і ![]() протилежно напрямлені.
протилежно напрямлені.
Розв’язання .
1. Знайдемо координати вектора ![]() :
: ![]() (х2-х1;у2-у1).Знайдемо координати вектора
(х2-х1;у2-у1).Знайдемо координати вектора ![]() :
: ![]() (х1-х2;у1-у2).
(х1-х2;у1-у2).
2. За теоремою про множення вектора на число: ![]() =λ
=λ![]() ;
; ![]() =(-1)
=(-1) ![]() ;
;
λ=-1<0. Отже, ![]() і
і ![]() протилежно напрямлені.
протилежно напрямлені.
№2. Доедіть, що вектори ![]() (1;2) і
(1;2) і ![]() (0,5;1) однаково напрямлені, а вектори
(0,5;1) однаково напрямлені, а вектори ![]() (-1;2) і
(-1;2) і ![]() (0,5;-1) протилежно напрямлені.
(0,5;-1) протилежно напрямлені.
Доведення.
1. ![]() (1;2),
(1;2), ![]() (0,5;1),
(0,5;1), ![]() =λ•
=λ•![]() . Знайдемо λ.
. Знайдемо λ.
![]() (1;2) =
(1;2) = ![]() (λ•1;λ•2)
(λ•1;λ•2)![]() λ=0,5.
λ=0,5.
Та як λ>0![]() вектори
вектори ![]() і
і ![]() однаково напрямлені.
однаково напрямлені.
2. ![]() (-1;2),
(-1;2), ![]() (0,5;-1),
(0,5;-1), ![]() =λ
=λ![]() . Знайдемо λ.
. Знайдемо λ.
![]() (-1;2)=
(-1;2)= ![]() (λ•(-1);λ•2)
(λ•(-1);λ•2)![]() λ•(-1)=0,5, λ•2=-1.
λ•(-1)=0,5, λ•2=-1.![]() λ=-0,5.
λ=-0,5.
Так як λ<0![]() вектори
вектори ![]() і
і ![]() протилежно напрямлені.
протилежно напрямлені.
Усні вправи : №516
Колективна робота учнів: №524, №527
Перевірочна самостійна робота.
Варіант I
1. Накресліть два вектора ![]() і
і ![]() так, що
так, що ![]() = 3 см,
= 3 см, ![]() = 2 см. Побудуйте
= 2 см. Побудуйте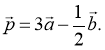
2. Чотирикутник KMNP – паралелограм. Виразіть через вектори ![]() і
і ![]() вектори
вектори ![]() і
і ![]() , де А – точка на стороні PN, така, що PA : AN = 2 : 1,
, де А – точка на стороні PN, така, що PA : AN = 2 : 1,
B – середина відрізка MN.
Варіант II
-
Накресліть два вектора
 і
і 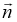 так, що
так, що 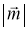 = 2 см,
= 2 см, 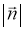 = 3 см.
= 3 см.
Побудуйте вектор 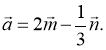
2. В паралелограмі ABCD точка M – середина сторони CD; N – точка на стороні AD, така, що AN : ND = 1 : 2. Виразіть вектори![]() і
і ![]() через вектори
через вектори ![]() і
і ![]() .
.
Варіант III
(група С)
1. В трикутнику ABC кут C = 90°, AC = 3 см, BC = 4 см.
Побудуйте вектор 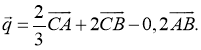
2. В трапеції ABCD AB || CD, AB = 3CD. Виразіть через вектори ![]() і
і ![]() вектори
вектори ![]() і
і ![]() , де M – середина сторони BC, а N – точка на стороні AB, така, що AN : NВ = 2 : 3.
, де M – середина сторони BC, а N – точка на стороні AB, така, що AN : NВ = 2 : 3.
V. Підбиття підсумків уроку
Запитання до класу
- Дайте означення множення вектора на число.
- Сформулюйте властивості добутку вектора на число
- Збираються зошити на перевірку, учням роздаються розв’язки відповідних варіантів для самоаналізу.
IV. Домашнє завдання
- Вивчити теоретичний матеріал §16
- Розв'язати задачі: №526, №529, або завдання з індивідуальних карток
-
Дано вектори
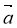 (3; 2) і
(3; 2) і 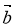 (0; -1). Знайдіть вектор
(0; -1). Знайдіть вектор 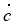 = -2
= -2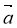 + 4
+ 4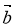 та його абсолютну величину.
та його абсолютну величину.
-
У паралелограмі ABCD О — точка перетину діагоналей, М — середина ВС. Виразіть
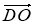 і
і 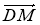 через вектори
через вектори 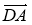 і
і 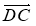 .
.
Урок №12
Тема уроку: Діі з векторами
Мета уроку:вдосконалювати вміння учнів виконувати дії з векторами, розв’язувати задачі на застосування основних означень і теорем; розвивати логічне мислення, культуру математичної мови і записів; виховувати самостійність, інтерес до математики, взаємодовіру.
Хід уроку
Тільки той,
хто не боїться великих невдач,
зможе досягти успіху.
Дж. Кенеді
І. Організаційний етап
Постановка цілей і завдань уроку: завдання уроку : вдосконалити вміння виконувати дії з векторами, розв’язувати задачі на застосування основних означень і теорем.
ІІ. Розминка «Чи готові до уроку?»
На екрані з’являються тестові завдання із домашньої роботи у різному порядку. Учням потрібно швидко, назвавши правило, обрати відповідь із запропонованих.
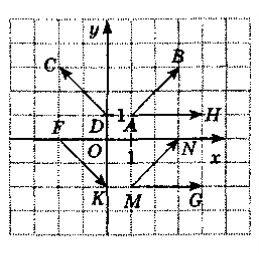 Тестова робота
Тестова робота
Користуючисьмалюнком,
виконайте завдання 1—6.
-
Знайдіть координати вектора
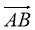 .
.
А (1; 1) Б (-2; 2) В (2; 2) Г (2; -2) -
Укажіть вектор, який дорівнює вектору
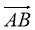 .
.
A ![]() Б
Б ![]() В
В ![]() Г
Г ![]()
-
Укажіть координати вектора
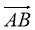 +
+ 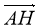 .
.
А (2; 5) Б (1; 2) В (5; 2) Г (1; -2)
-
Знайдіть
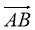 ∙
∙ 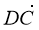 .
.
А ![]() Б 2 В 0 Г 1
Б 2 В 0 Г 1
-
При якому значенні вектори
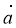 (1; -1) і
(1; -1) і  (п; 1) колінеарні?
(п; 1) колінеарні?
А Ні при яких п Б п = -1
В п = 1 Г п = ±1
- Знайдіть координати вершини D паралелограма ABCD, якщо А(0; 2), В(1; 0), С(2; 0).
А D(1; 2) Б D(2; 2) В D(1; -2) Г D(2; 1)
-
Знайдіть координати вектора
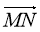 .
.
А(1; 1) Б (-2; 2) В (2; 2) Г(2; -2) -
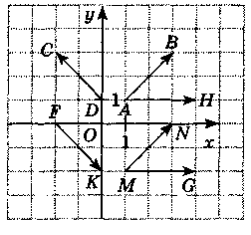 Укажіть вектор, який дорівнює вектору
Укажіть вектор, який дорівнює вектору 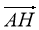 .
.
А ![]() Б
Б ![]() В
В ![]() Г
Г ![]()
-
Укажіть координати вектора
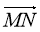 –
– 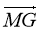 .
.
А (1; 2) Б(-1; 2) В (1; -2) Г(-1; -2)
-
Знайдіть
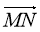 ∙
∙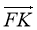 .
.
А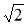 Б 2 В 0 Г 1
Б 2 В 0 Г 1
-
При якому значенні п вектори
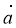 (-1; 1) і
(-1; 1) і  (п; -1) колінеарні?
(п; -1) колінеарні?
А n = 1 Б п = -1 В n = ±1 Г ні при яких п
-
При якому значенні п вектори
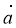 (1; -1) і
(1; -1) і  (п; 1) перпендикулярні?
(п; 1) перпендикулярні?
А Ні при яких n Б n = -1 В n = 1 Г n = ±1
ІІІ. Вдосконалення вмінь виконувати дії з векторами
Робота в парах за алгоритмом
Учням даються завдання + до окремих завдань даються детальні розв’язки, з метою, щоб учні самостійно могли перевірити правильність виконання завдань та зробити самоаналіз допущених помилок.
№ 1. Доведвіть, що для любих двох векторів ![]() і
і ![]() : (
: (![]() •
•![]() )2≤
)2≤ ![]() 2•
2•![]() 2 .
2 .
Доведення.
![]() •
•![]() =|
=| ![]() |• |
|• |![]() |cosα, тоді (
|cosα, тоді (![]() •
•![]() )2= |
)2= |![]() |2•|
|2•|![]() |2 cos2α,
|2 cos2α,
якщо -1≤сosα ≤1, тоді 0≤cos2α≤1, значить (![]()
![]() )2≤
)2≤![]() 2•
2•![]() 2.
2.
№ 2. Знайти кут між векторами ![]() (1;2),
(1;2), ![]() (1;-0,5).
(1;-0,5).
Розв’язання .
![]() •
•![]() =1•1+2•(-0,5)=0.
=1•1+2•(-0,5)=0.
![]() •
•![]() = |
= |![]() | |
| |![]() |cosα, звідси слідує, що
|cosα, звідси слідує, що
|![]() | |
| |![]() |cosα =0, cosα=0, так як
|cosα =0, cosα=0, так як ![]() ≠ 0,
≠ 0, ![]() ≠ 0, α=90˚
≠ 0, α=90˚
№3. Доведіть, що вектори ![]() (m;n) і
(m;n) і ![]() (-n;m) перпендикулярні, або обидва рівні нулю.
(-n;m) перпендикулярні, або обидва рівні нулю.
Доведення .
![]() •
•![]() = |
= |![]() | |
| |![]() | • cosα.
| • cosα. ![]() •
•![]() = -mn+mn=0. Звідси слідує, що cosα=0 або (
= -mn+mn=0. Звідси слідує, що cosα=0 або (![]() =0 і
=0 і ![]() =0),
=0), ![]() і
і ![]() перпендикулярні.
перпендикулярні.
№ 4. Дано вектори ![]() (1;0) і
(1;0) і ![]() (1;1). Знайдіть таке число λ, щоб вектор
(1;1). Знайдіть таке число λ, щоб вектор ![]() +λ
+λ![]() був перпендикулярний вектору
був перпендикулярний вектору ![]() .
.
Розв’язання .
Якщо ![]() і (
і (![]() +λ
+λ![]() ) перпендикулярні, тоді (
) перпендикулярні, тоді (![]() +λ
+λ![]() )•
)•![]() =0.
=0.
Розв’яжемо отримане рівняння : ![]() 2+λ
2+λ![]() •
•![]() =0, λ
=0, λ![]() •
•![]() = -
= -![]() 2, λ= - (
2, λ= - (![]() 2)/(
2)/( ![]() •
•![]() ).
).
![]() 2=1,
2=1, ![]() •
•![]() =1+1•0=1, λ=-1.
=1+1•0=1, λ=-1.
Додаткове завдання.
№5. Доведіть рівність ![]() 2=⌡
2=⌡![]() │2 ( скалярний квадрат вектора дорівнює квадрату його модуля)
│2 ( скалярний квадрат вектора дорівнює квадрату його модуля)
Розв’язання .
Нехай ![]() (а1;а2). Тоді |
(а1;а2). Тоді |![]() │=√а12+а22; ⌡
│=√а12+а22; ⌡![]() │2=а12+а22;
│2=а12+а22;
![]() 2=
2=![]() •
•![]() =(а1а2)•(а1а2)=а12+а22. Значить,
=(а1а2)•(а1а2)=а12+а22. Значить, ![]() 2=│
2=│![]() │2 .
│2 .
№6. Виведіть формулу квадрата суми двох векторів.
Розв’язання.
Тоді (![]() +
+![]() )2=(
)2=(![]() +
+![]() )•(
)•(![]() +
+![]() )=(
)=(![]() +
+![]() )•
)•![]() +(
+(![]() +
+![]() )•
)•![]() =
=![]()
![]() +
+![]()
![]() +
+![]()
![]() +
+![]()
![]() =
=![]() 2+2
2+2![]()
![]() +
+![]() 2.
2.
№7. Доведіть, що (![]() +
+![]() )(
)(![]() -
-![]() )=
)=![]() 2-
2-![]() 2.
2.
Обчисліть (![]() +
+![]() )(
)(![]() -
-![]() ), якщо │
), якщо │![]() │=3, │
│=3, │![]() │=5.
│=5.
Розв’язування задач біля дошки
1.Розв’язати задачу № 641 на дошці і в зошитах (для кута А пояснює вчитель):
Розв’язання
|
|
1) cos A =
|
![]()
![]()
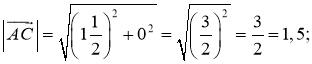
cos A = 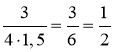 ; cos A =
; cos A = ![]() , то
, то ![]() A = 60°.
A = 60°.
2) cos B = 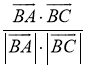 ;
; ![]()
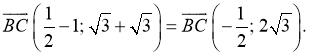
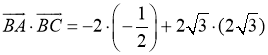 = 1 + 12 = 13;
= 1 + 12 = 13;
![]()
BC = 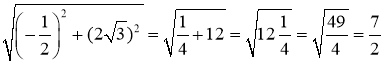 = 3,5;
= 3,5;
cos B = 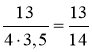 ≈ 0,9286;
≈ 0,9286; ![]() B знаходимо за таблицями Брадиса:
B знаходимо за таблицями Брадиса:
![]() B ≈ 21°47′.
B ≈ 21°47′.
3) ![]() C = 180° – 60° – 21°47′ ≈ 98°13′.
C = 180° – 60° – 21°47′ ≈ 98°13′.
відповідь: ![]() A = 60°;
A = 60°; ![]() B ≈ 21°47′;
B ≈ 21°47′; ![]() C ≈ 98°13′.
C ≈ 98°13′.
ІІІ. Підсумок уроку . «Дельта - плюс»
Учні спочатку висловлюють позитивні моменти уроку - « плюс», а потім про моменти які можна було замінити, або уникнути.цей метод навчає учнів дипломатично висловлювати свою думку, зважаючи на почуття оточуючих.
Що ми робили на уроці?
Навіщо ми це робили?
Чи досягли ви очікуваних результатів?
Чи працювали ви на завданнями разом(в групі , в парі)?
Чи узагальнювали видумки інших?
Чи доповнювали думки інших?
Чи вносили ви пропозиції, які були враховані в ході розв’язування?
ІV Домашнє завдання
§17-18 №644, №639, №654
Урок №11
Тема уроку: Діі з векторами
Мета уроку: виявити глибину учнівських знань, перевірити знання, вміння і навички учнів з теми «Вектори на площині» ; розвивати вміння мислити, застосовувати набуті знання до розв’язування вправ; виховувати самостійність, уміння самоорганізуватись.
Тип уроку: урок самостійної роботи.
Хід уроку
І. Організаційний етап
Повідомлення теми, мети і очікуваних результатів уроку. Коротка характеристика завдань самостійної роботи.
ІІ. Актуалізація опорних знань
Фронтальне опитування
З класом повторюються основні моменти теми «Вектори». Для цього дається завдання, пропонується учням відповідати по плану. Оцінюються відповіді.
1. Повторення теорії необхідної при розв'язанні задач. (проводиться у вигляді змагання між двома групами- рядами).
1) Означення вектора.
2) Координати вектора, як їх знайти.
3) Абсолютна величина вектора.
4) Сума і різниця векторів.
5) Добуток вектора на число.
6) Властивості колінеарних векторів.
7) Скалярний добуток векторів.
8) Що собою являє скалярний добуток векторів? (число чи вектор)
9) Якщо вектори перпендикулярні, що можна сказати про їх скалярний добуток? Чи вірне обернене твердження?
10) Косинус кута між векторами.
2. Задачі, які розв'язуються усно.
1) Вектор має кінець у точці А(![]() ; 0,3), а початок у точці В(0,3;
; 0,3), а початок у точці В(0,3; ![]() ).
).
Обчисліть координати даного вектора.
3) Знайдіть абсолютну величину вектора ![]() , якщо
, якщо![]() ?
?
4) Данo вектори ![]() (2; -1),
(2; -1), ![]() (-1 ; 3),
(-1 ; 3), ![]() (4; 0).
(4; 0).
Обчисліть різницю векторів ![]() +
+ ![]() і
і ![]() .
.
5) При якому значені b вектори ![]() (6; b) і
(6; b) і ![]() (5; -3) взаємно перпендикулярні
(5; -3) взаємно перпендикулярні
ІІІ. Виконання самостійної роботи
Текст контрольної роботи. Кожна правильна відповідь оцінюється в 3 бали.
Варіант 1
-
Знайдіть координати вектора
 =
=  – 2
– 2 , якщо
, якщо 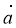 (1; 1),
(1; 1),  (3; 1).
(3; 1).
- Дано три вершини паралелограма ABCD: A(-2; 1), В(-1; 1), С(1; 1). Знайдіть координати вершини D.
-
Дано вектори
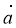 (4; 2) і
(4; 2) і  (x; -4). При якому значенні х ці вектори колінеарні?
(x; -4). При якому значенні х ці вектори колінеарні?
- Трикутник ABC задано координатами його вершин: А(-1; 1), В(0; 2), С(1; 1). Знайдіть зовнішній кут при вершині А.
Варіант 2
-
Знайдіть координати вектора
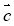 = 2
= 2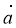 –
–  , якщо
, якщо 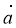 (1; 1),
(1; 1),  (3; 1).
(3; 1).
- Дано три вершини паралелограма ABCD: A(1; -3), В(2; -1), D(3; -3). Знайдіть координати вершини С.
-
Дано вектори
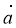 (4; 2) і
(4; 2) і  (x; -4). При якому значенні х ці вектори перпендикулярні?
(x; -4). При якому значенні х ці вектори перпендикулярні?
- Трикутник ABC задано координатами його вершин: А(3; 5), В(4; 6), С(5; 5). Знайдіть зовнішній кут при вершині А.
Варіант 3
-
Знайдіть координати вектора
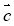 =
= 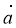 – 3
– 3 , якщо
, якщо 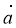 (-1; 2),
(-1; 2),  (1; -2).
(1; -2).
- Дано три вершини паралелограма ABCD: A(-4; 1), В(-1; 3), D(-2; 1). Знайдіть координати вершини С.
-
Дано вектори
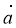 (2; 5) і
(2; 5) і  (-6; у). При якому значенні у ці вектори перпендикулярні?
(-6; у). При якому значенні у ці вектори перпендикулярні?
- Трикутник ABC задано координатами його вершин: А(1; 3), В(2; 4), С(3; 3). Знайдіть зовнішній кут при вершині А.
Варіант 4
-
Знайдіть координати вектора
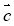 = 3
= 3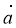 –
–  , якщо
, якщо 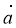 (-1; 2),
(-1; 2),  (1; -2).
(1; -2).
- Дано три вершини паралелограма ABCD: В(1; 3), С(-1;4), D(-2;2). Знайдіть координати вершини А.
-
Дано вектори
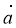 (2; 5) і
(2; 5) і  (-6; у). При якому значенні у ці вектори колінеарні?
(-6; у). При якому значенні у ці вектори колінеарні?
- Трикутник ABC задано координатами його вершин: А(0; 2), В(1; 3), С(2; 2). Знайдіть зовнішній кут при вершині А.
Відповіді та розв'язання до завдань тематичної контрольної роботи
Варіант 1
1. ![]() (1 – 2 ∙ 3; 1 – 2 ∙ 1) =
(1 – 2 ∙ 3; 1 – 2 ∙ 1) = ![]() (-5; -1). Відповідь.
(-5; -1). Відповідь. ![]() (-5; -1).
(-5; -1).
2. Нехай D(x; y), тоді ![]() (1; 0),
(1; 0), ![]() (1 – x; 1 – у) (рис. 213). Оскільки
(1 – x; 1 – у) (рис. 213). Оскільки ![]() =
= ![]() , то
, то 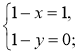
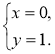 Отже, D(0; 1). Відповідь. D(0; 1).
Отже, D(0; 1). Відповідь. D(0; 1).
3. Вектори колінеарні, якщо ![]() , тоді х = -16, х = -8. Відповідь. х = -8.
, тоді х = -16, х = -8. Відповідь. х = -8.
4. ![]() (-2; 0),
(-2; 0), ![]() (1; 1) (рис. 214).
(1; 1) (рис. 214). 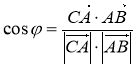 =
= 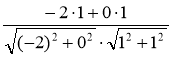 = =
= = 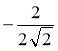 =
= ![]() =
= ![]() , звідси α = 135°. Відповідь. 135°.
, звідси α = 135°. Відповідь. 135°.
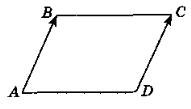
Варіант 2
1. ![]() (2 ∙ 1 – 3; 2 ∙ 1 – 1) =
(2 ∙ 1 – 3; 2 ∙ 1 – 1) = ![]() (-1; 1). Відповідь.
(-1; 1). Відповідь. ![]() (-1; 1).
(-1; 1).
2. Нехай С(х; у), тоді ![]() (1; 2),
(1; 2), ![]() (х – 3; у + 3) (рис. 215). Оскільки
(х – 3; у + 3) (рис. 215). Оскільки ![]() =
=![]() , то
, то 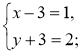
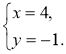 Отже, С(4; -1). Відповідь. С(4; -1).
Отже, С(4; -1). Відповідь. С(4; -1).
3. Дані вектори перпендикулярні, якщо 4 ∙ х + 2 ∙ (-4) = 0, тоді 4х – 8 = 0; 4х = 8; х = 2. Відповідь. 2.
4. ![]() (-2; 0),
(-2; 0), ![]() (1; 1), тоді (рис. 216)
(1; 1), тоді (рис. 216) 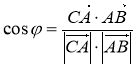 =
= 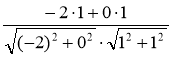 = =
= = 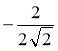 =
= ![]() =
= ![]() , звідси α = 135°. Відповідь. 135°.
, звідси α = 135°. Відповідь. 135°.
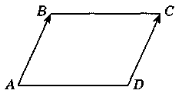
Варіант 3
1. ![]() (-1 – 3 ∙ 1; 2 – 3 ∙ (-2)) =
(-1 – 3 ∙ 1; 2 – 3 ∙ (-2)) = ![]() (-4; 8). Відповідь.
(-4; 8). Відповідь. ![]() (-4; 8).
(-4; 8).
2. Нехай С(х; у), тоді ![]() (3;2),
(3;2), ![]() (x + 2; y – 1) (рис. 217). Оскільки
(x + 2; y – 1) (рис. 217). Оскільки ![]() =
= ![]() , то
, то 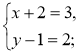
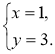 Отже, С(1; 3). Відповідь. С(1; 3).
Отже, С(1; 3). Відповідь. С(1; 3).
3. Дані вектори перпендикулярні, якщо 2 ∙ (-6) + 5 ∙ у = 0, звідси -12 + 5у = 0; 5у = 12; у = 2,4. Відповідь. 2,4.
4. ![]() (-1; -1),
(-1; -1), ![]() (2; 0) (рис. 218), тоді
(2; 0) (рис. 218), тоді
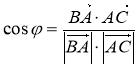 =
=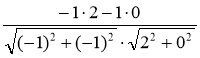 =
= 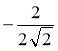 =
= ![]() =
= ![]() , звідси α = 135°. Відповідь. 135°.
, звідси α = 135°. Відповідь. 135°.
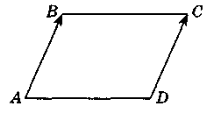
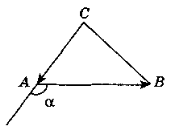
Варіант 4
1. ![]() (3 ∙ (-1) – 1; 3 ∙ 2 – (-2)) =
(3 ∙ (-1) – 1; 3 ∙ 2 – (-2)) = ![]() (-4; 8). Відповідь.
(-4; 8). Відповідь. ![]() (-4; 8).
(-4; 8).
2. Нехай А(х; у), тоді ![]() (1 – х; 3 – у),
(1 – х; 3 – у), ![]() (1; 2) (рис. 219). Оскільки
(1; 2) (рис. 219). Оскільки ![]() =
= ![]() , то
, то 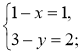
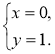 Отже, А(0; 1). Відповідь. А(0; 1).
Отже, А(0; 1). Відповідь. А(0; 1).
3. Вектори колінеарні, якщо ![]() , звідси 2у = -30; у = -15. Відповідь. -15.
, звідси 2у = -30; у = -15. Відповідь. -15.
4. ![]() (-1; -1),
(-1; -1), ![]() (2; 0) (рис. 220), тоді
(2; 0) (рис. 220), тоді
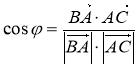 =
= =
= 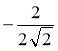 =
= ![]() =
= ![]() , звідси α = 135°. Відповідь. 135°.
, звідси α = 135°. Відповідь. 135°.
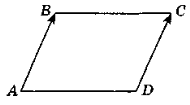
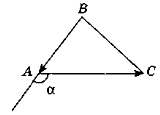
IV. Підсумок уроку
Звертається увага на завдання, які викликали забруднення.
Збираються зошити на перевірку.
V. Домашнє завдання
§16-19 (повторити основні означення,теореми і формули)
 Тестова робота
Тестова робота
Варіант 1
Користуючисьмалюнком,
виконайте завдання 1—6.
I рівень
-
Знайдіть координати вектора
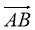 .
.
А (1; 1) Б (-2; 2) В (2; 2) Г (2; -2) -
Укажіть координати вектора -
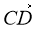 .
.
А (-2; 2) Б (2; -2); В (2; 2) Г (-2; -2)
-
Укажіть вектор, який дорівнює вектору
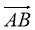 .
.
A ![]() Б
Б ![]() В
В ![]() Г
Г ![]()
II рівень
-
Укажіть координати вектора
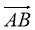 +
+ 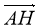 .
.
А (2; 5) Б (1; 2) В (5; 2) Г (1; -2)
-
Укажіть координати вектора
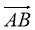 –
– 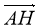 .
.
А (1; 2) Б (-1; 2) В (1; -2) Г(-1; -2)
-
Знайдіть
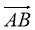 ∙
∙ 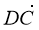 .
.
А ![]() Б 2 В 0 Г 1
Б 2 В 0 Г 1
ІІІ рівень
-
При якому значенні вектори
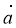 (1; -1) і
(1; -1) і  (п; 1) колінеарні?
(п; 1) колінеарні?
А Ні при яких п Б п = -1
В п = 1 Г п = ±1
-
При якому значенні п вектори
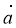 (1; 1) і
(1; 1) і  (п; 1) перпендикулярні?
(п; 1) перпендикулярні?
А п = 1 Б п = -1
В п = ±1 Г ні при яких п
- Знайдіть координати вершини D паралелограма ABCD, якщо А(0; 2), В(1; 0), С(2; 0).
А D(1; 2) Б D(2; 2) В D(1; -2) Г D(2; 1)
IV рівень
- Дано точки A(2; 1), B(3; 2), C(3; 1). Знайдіть внутрішній кут С трикутника ABC.
А 30° Б 45° В 60° Г 90°
- Знайдіть площу чотирикутника ABCD, якщо А(0; 1), В(1; 3), С(2; 1), D(1; -1).
А 2 Б 4 В 6 Г 8
-
Знайдіть кут А трикутника ABC, якщо А(0; 1), В(
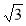 ; 2), С(
; 2), С(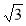 ; 1).
; 1).
А 30° Б 45° В 60° Г 90°
Варіант 2
Користуючисьмалюнком, виконайте завдання 1—6.
I рівень
-
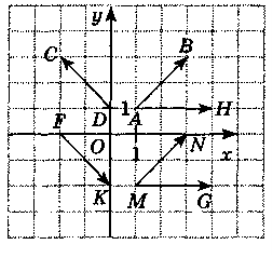 Знайдіть координати вектора
Знайдіть координати вектора 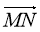 .
.
А(1; 1) Б (-2; 2) В (2; 2) Г(2; -2) -
2. Укажіть координати вектора -
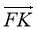 .
.
А (-2; 2) Б (2; -2); В (2; 2) Г (-2; -2) -
Укажіть вектор, який дорівнює вектору
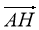 .
.
А ![]() Б
Б ![]() В
В ![]() Г
Г ![]()
II рівень
-
Укажіть координати вектора
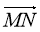 +
+ 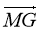 .
.
А (2; 5) Б (1; 2) В (5; 2) Г (1; -2)
-
Укажіть координати вектора
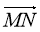 –
– 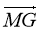 .
.
А (1; 2) Б(-1; 2) В (1; -2) Г(-1; -2)
-
Знайдіть
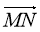 ∙
∙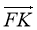 .
.
А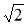 Б 2 В 0 Г 1
Б 2 В 0 Г 1
III рівень
-
При якому значенні п вектори
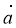 (-1; 1) і
(-1; 1) і  (п; -1) колінеарні?
(п; -1) колінеарні?
А n = 1 Б п = -1 В n = ±1 Г ні при яких п
-
При якому значенні п вектори
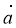 (1; -1) і
(1; -1) і  (п; 1) перпендикулярні?
(п; 1) перпендикулярні?
А Ні при яких n Б n = -1 В n = 1 Г n = ±1
- Знайдіть координати вершини А паралелограма ABCD, якщо В(1; 0), C(1; 1), D(-1; 0).
А А(2; 1) Б А(-1; -1) В А(0; 1) Г А(0; -1)
IV рівень
- Дано точки A(1; 1), В(2; 1), С(2; 2). Знайдіть внутрішній кут А трикутника ABC.
А 30° Б 45° В 60° Г 90°
- Знайдіть площу чотирикутника ABCD, якщо A(1; 1), В(2; 3), С(3; 1), D(2; -1).
А 2 Б 4 В 6 Г 8
-
Знайдіть кут В трикутника ABC, якщо А(0; -1), В(
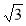 ; 0), С(
; 0), С(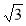 ; -1).
; -1).
А 30° Б 45° В 60° Г 90°
Відповіді до тестових завдань
|
Рівень |
Номер завдання |
Варіант 1 |
Варіант 2 |
|
І |
1 |
В |
В |
|
2 |
А |
А |
|
|
3 |
Б |
Г |
|
|
II |
4 |
В |
В |
|
5 |
Б |
Б |
|
|
6 |
В |
В |
|
|
III |
7 |
Б |
А |
|
8 |
Б |
В |
|
|
9 |
А |
Б |
|
|
IV |
10 |
Г |
Б |
|
11 |
Б |
Б |
|
|
12 |
А |
В |
Урок №2
Тема уроку: Модуль вектора, його напрям, рівність векторів
Мета уроку: розвивати вміння працювати самостійно і в групі. Розвивати самостійність пізнавальний інтерес. Виховувати такі людські якості, як сумлінність, здатність до переборення труднощів, працелюбство.
Тип уроку: урок комплексного застосування знань, умінь і навичок, урок самостійної роботи
Хід уроку
І. Організаційний етап.
Французький письменник Анатоль Франс (1844-1924) одного разу зауважив:« Вчитися можна тільки весело ... Щоб перетравлювати знання, треба поглинати їх з апетитом »
Так, давайте сьогодні на уроці будемо слідувати цій пораді письменника: будемо активні, уважні, будемо поглинати знання з великим бажанням, адже вони стануть в нагоді вам надалі.
ІІ. Актуалізація опорних знань і вмінь
Усні вправи . (Презентація №1, слайди 7-11 )
Учні працюють у групах (різнорівневі групи). У кожній групі є консультант, який в бланку обліку знань фіксує відповіді учнів. Правильна відповідь оцінюється в 1 бал. (максимум 7 балів)
- Заповни пропуски:
1. Вектор –це….., для якого …..початок, а … кінець .
2. Назви вектри зображені на малюнку: (Презентація №1, слайд 7)
3. Два ненульових вектора називаються колінеарними, якщо….. на паралельних … або ….. .
4. Два ненуьових вектора називаются співнапрямленими, якщо вони … і напрямлені … .
5. Назви співнапрямлені і протилежно напрямлені вектори (Презентація №1, слайд 9)
6. Два ненульових вектора називаються пролтилежно напрямленими, якщо вони …. і напрямлені… .
7. Вектори називаються рівними, якщо … і їх довжини…
8. № 449, №450
Застосуємо ці знання для розв’язання задач по готових кресленнях
Самостійна робота (Презентація №1, слайди 12-13 ) (учні за роботу отримують 4 бали. )Перевірка здійснюється вчителем.
- Які з векторів , зображених на малюнку:
- Співнапрямлені ;
- Протилежно напрямлені ;
- Мають рівні довжини?чи рівні при цьому самі вектори?
- На малюнку зображено паралелограм ABCD.Вкажіть вектори,довжини яких рівні. Чи рівні при цьому самі вектори?
ІІІ.Відпрацювання умунь інавичок
Робота в групах
На столах у кожної групи є картки з завданнями. Учні в групі попередньо обговорюють рішення завдання, потім представник від групи працює біля дошки, інші в зошиті. При розв’язуванні вправ учні користуються алгоритмом виправлення помилок. (вчитель виступає в ролі консультанта )
- Прочитайте завдання на картці.
- Задайте питання, якщо вони виникли .
- При виконанні завдання проявіть творчість.
- Кожне завдання оцінюється різною кількістю балів, залежно від складності.
А.П.Єршов «Геометрія 9 клас»
- №468(6 балів), №470
- №469(9 балів), №477
- №476 12 балів), №479
--- оцінюється робота учня, який працював біля дошки
IV. Рефлексія уроку.
Наш урок підійшов до кінця. Намалюйте в своїй роботі коло і підведемо підсумок. А підсумок підіб'ємо за допомогою старовинної притчі. Слухайте!
Йшов мудрець, а назустріч йому три чоловіка, які везли під сонцем візки з каменями для будівництва. Мудрець зупинився і поставив кожному по питанню. У першого запитав: «Що ти робив цілий день?» І той з усмішкою відповів, що цілий день возив кляті камені. У другого мудрець запитав: «А ти, ч то робив цілий день?» І той відповів: «А я сумлінно виконував свою роботу». А третій посміхнувся, його обличчя засвітилося радістю і задоволенням: «А я брав участь в будівництві храму».
Діти , давайте спробуємо оцінити кожен свою роботу за урок.
- Хто працював, як перша людина, зафарбовує коло синім кольором.
- Хто працював сумлінно - зеленим.
- Хто брав участь в будівництві храму - червоним.
VІ. Домашнє завдання.
Вивчити §14 пункт 14.1- 14.2
Випереджаюче завдання §16 пункт 16.3
Повторити формулу знаходження довжини відрізка.
1.Скільки векторів можна провести використовуючи дані точки?
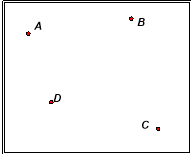 Група А: Знайти периметр трикутника, складеного із векторів, якщо /АВ/=12 см, /ВС/ = 17 см і /АС/ = 20 см.
Група А: Знайти периметр трикутника, складеного із векторів, якщо /АВ/=12 см, /ВС/ = 17 см і /АС/ = 20 см.
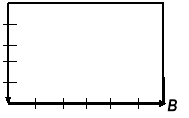 Група В: Чому рівна площа прямокутника, зображеного векторами, якщо модулі векторів показані штрихами.
Група В: Чому рівна площа прямокутника, зображеного векторами, якщо модулі векторів показані штрихами.
 Група С: Знайти модуль вектора АВ, зображеного на малюнку
Група С: Знайти модуль вектора АВ, зображеного на малюнку
![]()
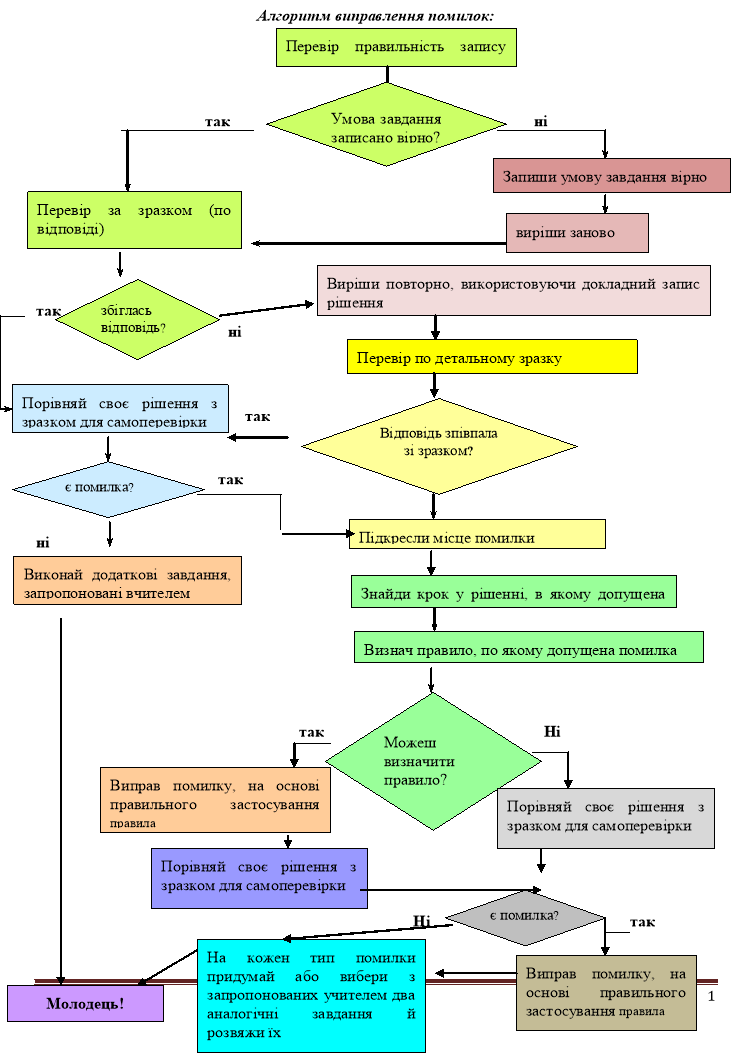
Урок №4
Тема уроку: Сума трьох і більше векторів.
Мета уроку:Формувати поняття суми трьох і більше векторів, навчити будувати суму двох і декількох векторів, використовуючи правило багатокутника, вчити розв'язувати задачі.
Розвивати логічне мислення, увагу, пам'ять, розумову активність, пізнавальний інтерес.
Виховувати зібраність самовладання, комунікативність (вміння працювати в колективі)
Обладнання : властивості додавання векторів (таблиці)
Тип уроку:урок комплексного застосування знань і вмінь з елементами групової роботи.
Хід уроку
І. Організаційний етап.
Формула успіху:
1% везіння
+ 99% потіння
У С П І Х
(Едісон)
Тому на уроці ми намагатимемось досягти такої ж відповіді .
- Перевірка домашнього завдання .
На перерві перевіряються зошити у одного з представників груп, вони, в свою чергу перевіряють у останній, і про результати перевірки доповідають вчителю на початку уроку. ( по потребі на дошці ведеться детальний запис розв’язання Д/З)
Успіх – це результат певних умінь і навичок
ІІ. Акктуалізація опорних знань. (Презентація №1, слайди 19-23 )
- Самостійна робота
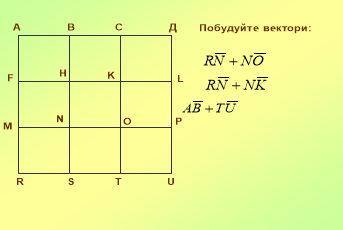 І варіант І І варіант
І варіант І І варіант
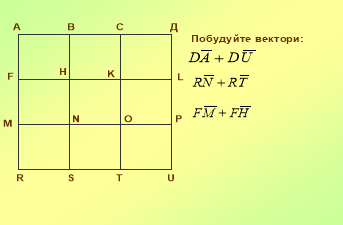
- «Мозкова атака» (Презентація №1, слайди 24-26 )
Розв’язування вправ на застосування властивостей суми векторів. Кожен учень працює самостійно над проблемою (задачами). По перебігу 3-5 хв. учні пропонують розв’язання задач . Той учень, який найкраще і найшвидше розв’язав задачу , має право захистити свій розв’язок біля дошки.(учні обирають задачі в довільному порядку).
№1. Доведіть, що ![]() .
.
Доведення:
![]()
![]()
![]() , рівність вірна.
, рівність вірна.
№2. Спростіть вираз:
1) ![]() ; 2)
; 2) ![]() .
.
Розв’язання:
Використаємо властивості векторів:
![]() 1)
1) ![]() ;
;
2) ![]() .
.
№3. Знайдіть вектор ![]() із умови:
із умови:
1) ![]() ; 2)
; 2) ![]() .
.
Розв’язання:
Використаємо властивості векторів:
1) ![]() ;
;
2) ![]() ;
;
![]() або ж
або ж
![]() , тоді
, тоді ![]() .
.
№4. Доведіть, що чотирикутник ABCD –
паралелограм, якщо![]() , де Р і х –довільні точки площини.
, де Р і х –довільні точки площини.
Доведення:
![]()
![]()
![]() ;
;
![]() , отримаємо, що вектори
, отримаємо, що вектори ![]() і
і ![]() рівні, а це означає,
рівні, а це означає,
що![]() і
і ![]() , тоді за означенням парллелограма ABCD – паралелограм.
, тоді за означенням парллелограма ABCD – паралелограм.
ІІІ. Тема уроку
Пояснення нового матеріалу (конспектування)
(Презентація №1, слайди 27-28 )
Правило многокутника: якщо A1, A2, .., An –довільні точки площини, то ![]() .
.
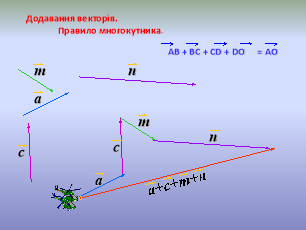 При додаванні декількох векторів сума даних векторів може дорівнювати нульовому вектору, якщо початок першого вектора збігається з кінцем останнього вектора.
При додаванні декількох векторів сума даних векторів може дорівнювати нульовому вектору, якщо початок першого вектора збігається з кінцем останнього вектора.
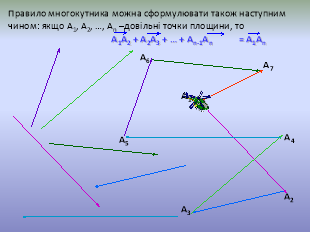
ІІІІ. Закріплення
Застосування інтерактивних методів «Навчаючись - учусь», «Робота в групах»
(Презентація №1, слайди 29-32 )
Учні об’єднані у три групи. Кожна група отримує по шість однакових завдань.
Кожен учень групи вибирає собі одне і розв’язує його, після цього пояснює розв’язання учням групи. За кожне завдання група отримує по два бали. У кожній групі є учень-консультант. Він коригує роботу в групі та може консультувати учнів інших членів групи.
Зібратися разом – це початок, працювати разом – це успіх.
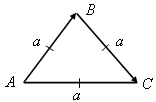 Задача №1: Дано трикутник АВС .знайти довжину вектора АС
Задача №1: Дано трикутник АВС .знайти довжину вектора АС
Розв’язання ![]() = a.
= a.
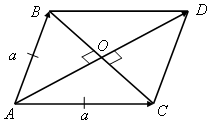 Відповідь : а.
Відповідь : а.
Задача №2: Знайти ![]() .
.
Розвязання:
Знайдемо суму векторів ![]() і
і ![]() по правилу паралелограма:
по правилу паралелограма: ![]() ; знайдемо довжину вектора
; знайдемо довжину вектора ![]() .
.
За умовою AB = AC = a, то ABDC – ромб; діагоналі ромба взаємно перпендикулярні: AD ![]() BC і точкою перетину діляться навпіл ,
BC і точкою перетину діляться навпіл ,
тоді BO = OC = ![]() і AO = OD. Із прямокутного трикутника AOC за теоремою Піфагора знайдемо AO:
і AO = OD. Із прямокутного трикутника AOC за теоремою Піфагора знайдемо AO:
AO = 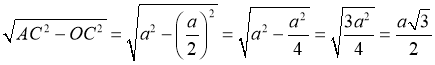 ;
;
AD = 2AO = 2![]() = a
= a![]() . Отже,
. Отже, ![]() = a
= a![]() .
.
Відповідь : a![]() .
.

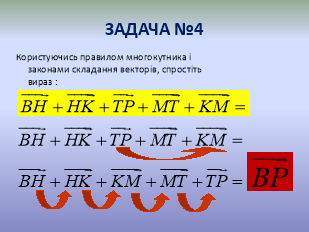

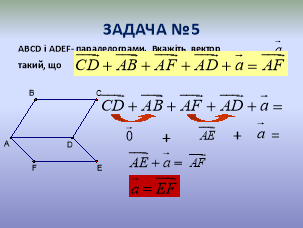
Самостійна робота (навчального характеру).
Варіант I
1. Накресліть чотири вектора так, щоб вони не лежали на паралельних прямих
![]() . Побудуйте вектор
. Побудуйте вектор ![]() .
.
2.Спростіть вираз : ![]() .
.
Варіант ІІ
1. Накресліть п’ять векторів так, щоб вони не лежали на паралельних прямих
![]() . Побудуйте вектор
. Побудуйте вектор ![]() .
.
2. Спростіть вираз: ![]() .
.
 IV. Підсумок уроку(Презентація №1, слайди33-34)
IV. Підсумок уроку(Презентація №1, слайди33-34)
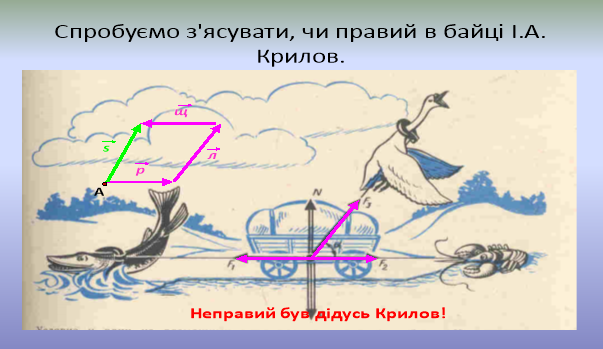
V. Домашнє завдання §15 №490(а), №495(а,б), №502(а,б)
УРОК № 7
Тема уроку. Колінеарні вектори.
Мета уроку: формування поняття «колінеарні вектори»; вивчення властивості та ознаки колінеарних векторів; формування навичок розкладання вектора за двома не колінеарними векторами, сприяти розвитку спостережливості, здатності узагальнювати і робити висновки, виховання працелюбності.
Обладнання: опорні конспекти, варіанти самостійної роботи
Тип уроку: урок знайомства з новим матеріалом
Хід уроку
- Організаційний етап.
Перевірка домашнього завдання
Правильність виконання домашніх завдань перевірити за записами на дошці, які зроблено до початку уроку.
Математичний диктант
Дано вектори:
Варіант 1 Варіант 2
![]() (3; 0);
(3; 0); ![]() (7; 4)
(7; 4) ![]() (-2; 2);
(-2; 2); ![]() (1; 6)
(1; 6)
Запишіть:
а) координати вектора ![]() +
+ ![]() ;
;
б) координати вектора ![]() –
– ![]() ;
;
в) координати вектора ![]() –
– ![]() ;
;
г) довжину вектора ![]() –
– ![]() ;
;
д) координати вектора 2![]() –
– ![]() ;
;
є) довжину вектора 2![]() –
– ![]() .
.
- Сприймання й усвідомлення нового матеріалу
Повідомлення теми і цілей уроку, мотивація
Урок присвячений поняттю колінеарних векторів. Воно дасть можливість розкладати вектор за двома не колінеарними векторами і вирішувати завдання виду:
Дано паралелограм АВСD, О - точка перетину діагоналей. Виразіть:
а) вектор ![]() через вектор
через вектор ![]() ,
,
б) ![]() через
через ![]() ,
,
в) знайдіть k, якщо ![]() =k•
=k•![]() .
.
Пояснення нового матеріалу (бесіда)
Два ненульових вектора називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих

![]()
![]()

Колінеарні вектори або однаково напрямленіі, або протилежно напрямлені.
Нехай ![]() і
і ![]() - відмінні від нуля колінеарні вектори.
- відмінні від нуля колінеарні вектори.
Доведемо, що існує таке число λ таке, що ![]() =λ
=λ![]() .
.
Доведення.
Припустимо , вектори ![]() і
і ![]() однаково напрямлені. Вектори
однаково напрямлені. Вектори ![]() і (|
і (|![]() |/ |
|/ |![]() |) а однаково напрямлені і мають одну и ту ж абсолютну величину
|) а однаково напрямлені і мають одну и ту ж абсолютну величину ![]() .
.
Значить, вони рівні ![]() = (|
= (|![]() |/|
|/|![]() |)•
|)•![]() =λ
=λ![]() , λ= |
, λ= |![]() |/ |
|/ |![]() |. У випадку протилежно напрямлених векторів
|. У випадку протилежно напрямлених векторів ![]() і
і ![]() аналогічно робимо висновок, що
аналогічно робимо висновок, що ![]() = - (|
= - (|![]() | /|
| /|![]() |)•
|)• ![]() = λ
= λ![]() , λ = -|
, λ = -| ![]() | / |
| / |![]() |.
|.
Нехай ![]() і
і ![]() - відмінні від нуля неколинеарні вектори.
- відмінні від нуля неколинеарні вектори.
Доведемо, що довільний вектор ![]() можна представити
можна представити
у вигляді ![]() =λ
=λ![]() +μ
+μ![]() .
.
Доведення .
Нехай А і В - початок і кінець вектора .
С
![]()


![]()
![]()
![]()
![]() А
А ![]() В
В
Проведемо через точки А і В прямі, паралельні векторам ![]() і
і ![]() . Вони перетнуться в деякій точці С. Маємо:
. Вони перетнуться в деякій точці С. Маємо: ![]() =
=![]() +
+![]() . Так як вектори
. Так як вектори ![]() і
і ![]() колінеарні, то
колінеарні, то ![]() =λ
=λ![]() . Так як вектори
. Так як вектори ![]() і в колінеарні, то
і в колінеарні, то ![]() = μ
= μ![]() . Таким чином,
. Таким чином, ![]() = λ
= λ![]() +μ
+μ![]() .
.
Властивість колінеарних векторів:
Якщо вектори колінеарні, то їхні відповідні координати пропорційні. І навпаки, якщо відповідні координати двох векторів пропорційні, то ці вектори колінеарні.
Якщо вектори ![]() (a1; a2) і
(a1; a2) і ![]() (b1; b2) колінеарні,
(b1; b2) колінеарні,
то ![]() . Якщо
. Якщо ![]() і
і ![]() (a1; a2),
(a1; a2), ![]() (b1; b2),
(b1; b2),
то вектори ![]() і
і ![]() колінеарні.
колінеарні.
ІІІ. Розв’язування вправ на вироблення практичних навичок по темі
Колективне виконання вправ
-
Серед векторів
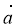 (-2; 4),
(-2; 4), 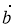 (2; 2),
(2; 2), 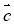 (0; -1),
(0; -1), 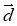 (1; -2) знайдіть колінеарні(№530)
(1; -2) знайдіть колінеарні(№530)
Розв'язання
Оскільки вектори колінеарні, якщо їхні відповідні координати пропорційні, то маємо ![]() = -2, звідси вектори
= -2, звідси вектори ![]() i
i ![]() колінеарні.
колінеарні.
Відповідь:![]() i
i ![]() .
.
-
Знайдіть довжину вектора
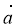 (6; у), якщо він колінеарний вектору
(6; у), якщо він колінеарний вектору 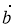 +
+ 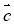 , де
, де 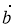 (-2; 0),
(-2; 0), 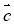 (0; 1).
(0; 1).
Розв'язання
Нехай ![]() +
+ ![]() =
= ![]() , тоді
, тоді ![]() (-2 + 0; 0 + 1) =
(-2 + 0; 0 + 1) = ![]() (-2; 1). Оскільки вектори
(-2; 1). Оскільки вектори ![]() і
і ![]() колінеарні, то
колінеарні, то ![]() , звідси у =
, звідси у = ![]() = -3, тоді
= -3, тоді ![]() (6; -3) і
(6; -3) і ![]() =
= ![]() = =
= = ![]() =
= ![]() =
= ![]() = 3
= 3![]() .
.
Відповідь: 3![]()
Повернемося до задачі, яка пропонувалась на початку уроку.
Дано паралелограм АВСD, О - точка перетину діагоналей.
Виразіть: а) вектор ![]() через вектор
через вектор ![]() ; б) вектор
; б) вектор ![]() через вектор
через вектор ![]() ; в) знайдіть κ, якщо:
; в) знайдіть κ, якщо: ![]() =κ•
=κ•![]() ,
, ![]() =κ•
=κ•![]() ,
, ![]() =κ•
=κ•![]() ,
, ![]() =κ•
=κ•![]() .
.
Розв’язання .
Вектори ![]() і
і ![]() колінеарні, так як лежать на одній прямій. Так як О - точка перетину діагоналей паралелограму, то
колінеарні, так як лежать на одній прямій. Так як О - точка перетину діагоналей паралелограму, то ![]() =
=![]() •
•![]() , λ=
, λ=![]() .
. ![]() і
і ![]() протилежно напрямлені , тоді
протилежно напрямлені , тоді ![]() = -
= - ![]() . Отже , якщо
. Отже , якщо ![]() =
=![]()
![]() , то
, то ![]() = -
= -![]() •
•![]() , λ= -
, λ= - ![]() . Використовуючи властивість диагоналей паралелограма і поняття розкладання двох колінеарних векторів , отримуємо:
. Використовуючи властивість диагоналей паралелограма і поняття розкладання двох колінеарних векторів , отримуємо: ![]() =κ•
=κ•![]() , κ=
, κ=![]() ;
; ![]() =κ•
=κ•![]() , κ=2;
, κ=2; ![]() =κ•
=κ•![]() , κ=2;
, κ=2; ![]() =κ•
=κ•![]() , κ=1.
, κ=1.
Самостійне виконання вправ (№545)
- Визначте, чи колінеарні вектори:
а) ![]() (2; 3) і
(2; 3) і ![]() (-4; 6); б)
(-4; 6); б) ![]() (1; 3) і
(1; 3) і ![]() (-3; -9).
(-3; -9).
- При якому значенні m вектори (15; m) і (18; 12) колінеарні?
-
Чи колінеарні вектори
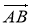 і
і 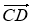 , якщо А(3; -2), B(-1; 4), C(1; 3), D(-3; 9)?
, якщо А(3; -2), B(-1; 4), C(1; 3), D(-3; 9)?
-
При якому значенні n вектори
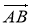 і
і 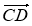 колінеарні, якщо А(1; 0), В(3; п), С(2; 2), D(5; 4)?
колінеарні, якщо А(1; 0), В(3; п), С(2; 2), D(5; 4)?
ІV. Підбиття підсумків уроку
Запитання до класу
- Які вектори називаються колінеарними?
- Сформулюйте ознаку колінеарності векторів.
- Сформулюйте властивість координат колінеарних векторів
- Перегляньте теоретичний матеріал підручника і доповніть вдома конспект.
V. Домашнє завдання
- Вивчити теоретичний матеріал §16.1,
- Розв'язати задачі №530, №546
-
Відомо, що вектори
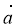 (1; -1) і
(1; -1) і 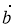 (-2; m) колінеарні. Знайдіть m.
(-2; m) колінеарні. Знайдіть m.
-
Серед векторів
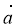
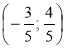 ,
, 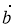
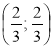 ,
, 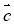 (0; 1),
(0; 1), 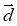
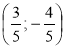 знайдіть одиничні і зазначте, які з них колінеарні.
знайдіть одиничні і зазначте, які з них колінеарні.


про публікацію авторської розробки
Додати розробку