Стаття "Аналіз планіметричного матеріалу 8 класу"

Аналіз планіметричного матеріалу 8 класу

 У 8 класі учні ознайомлюються з різними видами чотирикутників і їх властивостями, розглядають вписані та центральні кути, вписані й описані чотирикутники та інші многокутники. Ознайомлюються з двома перлинами геометрії – теоремою Фалеса і теоремою Піфагора. Розглянувши подібність трикутників і площі фігур, учні переконуються, наскільки широко геометрія використовується в нашому житті.

 Вивчаючи матеріал розділу «Чотирикутники», доцільно демонструвати учням на дошці рисунки чотирикутників і їх видів при введенні означень. В підручнику «Геометрія» 8 клас Г. П. Бевза розглядається рисунок, на аналізі якого робиться висновок про поняття чотирикутника. О. В. Погорєлов дає чітке означення цього поняття: «Чотирикутником називається фігура, яка складається з чотирьох точок і чотирьох відрізків, що послідовно їх сполучають. При цьому жодні три з даних точок не повинні лежати на одній прямій, а відрізки, які їх сполучають, не повинні перетинатись» [2].

 Означення паралелограма, прямокутника, ромба, квадрата, трапеції та введення їх властивостей пояснюється за допомогою рисункових засобів. Це добре показано в підручниках О. В. Погорєлова, Г. П. Бевза та М. І. Бурди для 8 класу.

 Логічне роз’яснення теореми Фалеса закріплено О. В. Погорєловим: «Якщо паралельні прямі, які перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки і на другій його стороні (рис. 1).

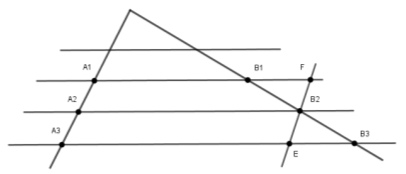
Рис. 1

Доведення. Нехай А₁, А₂, А₃ – точки перетину паралельних прямих з однією із сторін кута і А₂ лежить між А₁ і А₃ (рис. 1). Нехай В₁, В₂, В₃ – відповідні точки перетину цих прямих з другою стороною кута. Доведемо, що коли А₁А₂ = А₂А₃, то В₁В₂ = В₂В₃.

Проведемо через точку В₂ пряму EF, паралельну прямій А₁А₃. За властивістю паралелограма А₁А₂ = FВ₂, А₂А₃ = В₂E. Оскільки А₁А₂ = А₂А₃, то    FВ₂ = В₂E.

Трикутники В₂В₁F і В₂В₃E рівні за другою ознакою. У них В₂F = В₂E за доведенням. Кути при вершині В₂ рівні як вертикальні, а кути В₂FВ₁ і В₂EВ₃ рівні як внутрішні різносторонні при паралельних прямих А₃В₃ і А₁В₁ і січній EF. З рівності трикутників випливає рівність сторін: В₁В₂ = В₂В₃. Теорему доведено.

Зауваження. В умові теореми Фалеса замість сторін кута можна взяти довільні дві прямі, при цьому висновок теореми буде таким самим: паралельні прямі, які перетинають дві дані прямі і відтинають на одній прямій рівні відрізки, відтинають рівні відрізки і на другій прямій» [8].

Теорема Піфагора – одна з найцікавіших і найважливіших теорем геометрії. Доводити її можна різними способами, найкраще – з використанням властивостей подібних трикутників. Метричні співвідношення в прямокутному трикутнику, теорему Піфагора і теорему, обернену до неї, корисно пояснювати учням, використовуючи рисункові засоби. Наприклад, доведенням теореми Піфагора займалось багато математиків протягом століть. Нині є понад 150 різних доведень цієї теореми. Так, індійський математик Бхаскара (ХІІ ст.) запропонував таку фігуру, як на рисунку 2.2.3, без жодних пояснень. Під рисунком стоїть лише одне слово – «дивись» [3].

Нині встановлено, що цю теорему застосовували за 1500 років до Піфагора в давньому Вавилоні. Теорема була сформульована так: площа квадрата, побудованого на гіпотенузі прямокутного трикутника, дорівнює сумі площ квадратів, побудованих на катетах (рис. 4).

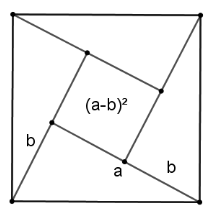
Рис. 3

В наші дні математики-методисти дають більш чітке формулювання цієї теореми, але й їх ґрунтування не обходяться без використання рисункових засобів.

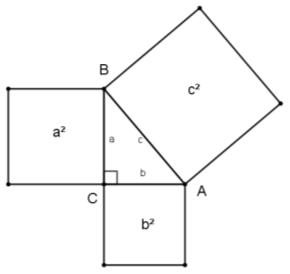
Рис. 4

 В підручнику «Геометрія» О. В. Погорєлова для 8 класу подається розділ «Декартові координати на площині». Автор доцільно подає означення декартових координат, які розглядаються на основі рисункових засобів. Наприклад, за допомогою рисунка вводиться поняття осі координат (перпендикулярні прямі х і у), вісь абсцис (вісь х), вісь ординат (вісь у) та початок координат (точка перетину осей О) (рис. 5).

 Координати середини відрізка, відстань між точками, рівняння кола, рівняння прямої, координати точки перетину прямих, розміщення прямої відносно системи координат, кутовий коефіцієнт у рівнянні прямої, графік лінійної функції, перетин прямої з колом розглянуті та обґрунтовані за допомогою рисунків.

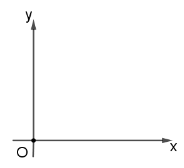
Рис. 5

 Координатний метод у геометрії виявися настільки зручним і корисним, що започаткував створення окремої великої частини математики – аналітичної геометрії. За допомогою аналітичної геометрії вдалося перекинути міст між алгеброю і геометрією [4].

Вивчаючи розділ «Рух» варто звернути увагу на те, що роз’яснення цієї теми повністю орієнтоване на рисункових засобах в усіх підручниках з геометрії. Наприклад, О. В. Погорєлов подає визначення поняття перетворення, на основі якого формулює визначення руху: «Перетворенням однієї фігури в іншу називається рухом, якщо воно зберігає відстань між точками, тобто переводить будь-які дві точки Х  і Y першої фігури у точки Х', Y' другої фігури так, що ХY = Х'Y' (рис. 6).

 Зауваження. Поняття руху в геометрії пов’язане із звичайним уявленням про переміщення. Але якщо, говорячи про переміщення, ми уявляємо неперервний процес, то в геометрії для нас матиме значення тільки початкове і кінцеве положення фігури» [8].

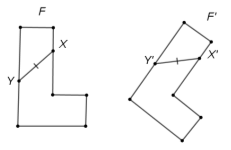
Рис. 6

 Вектор – одне з фундаментальних понять математики. Цікавою та складною є історія його виникнення та розвитку. Принаймні три джерела створювали основу і надавали сил векторному численню. Це – геометричне (числення відрізків), механічне (дослідження векторних величин) і алгебраїчне (теорія кватерніонів). Найбільш загальна теорія векторів побудована на початку ХХ століття на аксіоматичній основі [3].

 О. В. Погорєлов формулює чітке визначення вектора: «Вектором називатимемо напрямлений відрізок (рис. 7)» [8].

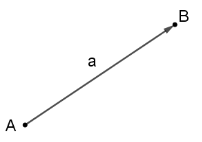
Рис. 7

 Під час пояснення матеріалу, що стосується дій над векторами, найдоцільніше використати рисункові засоби для кращого запам’ятовування відповідних правил. Так, пояснюючи учням поняття скалярного добутку векторів та його доведення, вчитель демонструє рисунок: «Скалярний добуток векторів дорівнює добутку їх абсолютних величин на косинус кута між ними.

Доведення. Нехай і – дані вектори і φ – кут між ними. Маємо:         = = + = + + + =     = + 2 + , або = + + 2.

Звідси видно, що скалярний добуток виражається через довжини векторів , і , а тому не залежить від вибору систему координат, тобто скалярний добуток не зміниться. якщо систему координат вибрати спеціально. Візьмемо систему координат xy так, як показано на рисунку 2.2.8. За таким вибором системи координат координатами вектора будуть і 0, а координатами вектора будуть cos φ і sin φ. Скалярний добуток =       = cos φ + 0sin φ = cos φ. Теорему доведено» [8].

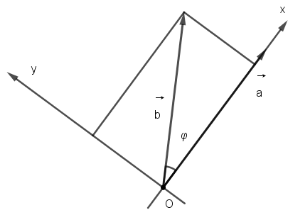
Рис. 8

 За допомогою векторного методу зручно характеризувати геометричні та інші об’єкти та співвідношення між ними. Саме тому вектори ефективно використовуються у математиці, фізиці, астрономії та інших природничих науках.

 Розглянемо нестандартні планіметричні задачі курсу 8 класу.

 Задача 1. Великий прямокутник має розміри 12 16, а затінений – a 12 (рис. 9). Діагоналі цих прямокутників взаємно перпендикулярні. Чому дорівнює a? [6]

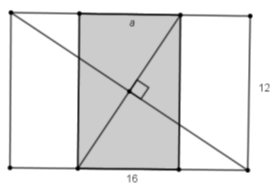
Рис. 9

 Розв’язання. Оскільки CAD = EAB = FBE = GBH, то tg CAD =   = tg GBH або = . Звідки a = 9.

Задача 2. У прямокутному трикутнику катети дорівнюють 12 см і 5 см. Знайти відстань між центрами вписаного і описаного кіл [5].

Розв’язання. Нехай АВС – заданий трикутник, C = 90 (рис. 10). Введемо прямокутну систему координат так, щоб її початок співпадав з точкою

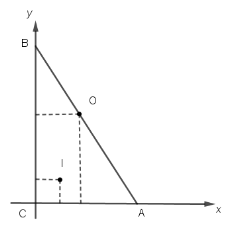
Рис. 10

С, а катети лежали на координатних осях. Тоді А(5;0), В(0;12).

 Знаходимо, що радіус вписаного кола r = 2 см, тоді центр вписаного кола І(2;2). Середина О гіпотенузи АВ є центром кола, описаного навколо прямокутного трикутника. Тому О(2,5;6). Отже, відстань ОІ = см.

 Задача 3. Нехай ABCD – рівнобедрена трапеція з меншою основою ВС (рис. 11). Точки M і N – середини сторін АВ і AD відповідно, а відрізок ВР – висота трапеції ABCD. Позначимо через Q точку перетину відрізків DM і BN. Довести, що точки Р, Q і С належать одній прямій [9].

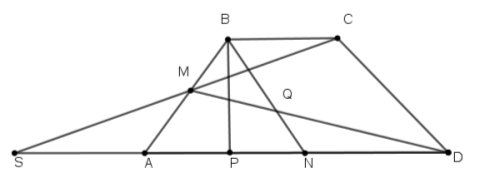
Рис. 11

 Розв’язання. Точка Q є точкою перетину медіан DM і BN трикутника ABD, тому DQ = DM.

 Нехай точка S = MС AD. Тоді АS = ВС, SМ = МС, SР = РD, тобто DМ і СР є медіанами трикутника SСD. З умови DQ = DM випливає, що точка Q також є точкою перетину медіан трикутника SСD, звідки випливає, що точка Q належить прямій СР.

 Отже, рисункові засоби, які використовуються при поясненні тих чи інших понять, теорем та властивостей курсу 8 класу покращать засвоєння учнями геометричного матеріалу, а вчителю допоможуть зекономити час, завдяки чому більше розв’язати планіметричних задач, що сприятиме розвитку в учнів інтересу до геометрії.

Список використаної літератури

1. Бевз Г. П. Геометрія: підруч. для 7 кл. загальноосвіт. навч. закл. / Г. П. Бевз, В. Г. Бевз, Н. Г. Владімірова. – К.: Вид-во «Відродження», 2015. – 192 с.
2. Бевз Г. П. Геометрія: підруч. для 8 кл. загальноосвіт. навч. закл. / Г. П. Бевз, В. Г. Бевз, Н. Г. Владімірова. – К.: Видавничий дім «Освіта», 2016. – 272 с.
3. Бевз Г. П. Геометрія: підруч. для 9 кл. загальноосвіт. навч. закл. / Г. П. Бевз, В. Г. Бевз, Н. Г. Владімірова. – К.: Видавничий дім «Освіта», 2017. – 272 с.
4. Бурда М. І. Геометрія: підруч. для 9 кл. загальноосвіт. навч. закл. /              М. І. Бурда, Н. А. Тарасенкова. – К.: Вид-во «Зодіак-ЕКО», 2009. – 240 с.
5. Міжнародний математичний конкурс «Кенгуру – 2008»: Інформаційний вісник / Уклали: А. С. Добосевич, М. С. Добосевич, Р. Є. Кокорузь,              О. Б. Таратула. – Львів: Каменяр, 2008. – 70 с.
6. Міжнародний математичний конкурс «Кенгуру – 2009»: Інформаційний вісник / Уклали: А. С. Добосевич, М. С. Добосевич, О. М. Добосевич,          Р. Є. Кокорузь, О. Б. Таратула. – Львів: Каменяр, 2009. – 56 с.
7. Міжнародний математичний конкурс «Кенгуру – 2011»: Інформаційний вісник / Кенгуру – 2011, міжнародний математичний конкурс; уклали:        А. С. Добосевич, М. С. Добосевич, О. М. Добосевич, Р. Є. Кокорузь,           О. Б. Таратула. – Львів: Каменяр, 2011. – 54 с.
8. Погорєлов О. В. Геометрія: Планіметрія: Підруч. для 7-9 кл. загальноосвіт. навч. закл. – 7-ме вид. – К.: Школяр, 2004. – 240 с.
9. Сарана О. А. Математичні олімпіади: просте і складне поруч: Навч. посібник. 2-ге видання, доп. – Тернопіль: Навч. книга – Богдан, 2011. –     400 с.