Стаття "Елементи теорії ймовірності"

                                                             Овчар Ольга, вчитель математики        

                                                              вищої категорії сзш №67 м.Львова

 

                           Елементи теорії ймовірності

 

У статті висвітлюються питання вивчення теорії ймовірності  в середній школі, дається короткий аналіз застосування елементів комбінаторики до розв’язування задач на знаходження ймовірності подій.

 Актуальність проблеми.

Теорія ймовірності, як і будь-яка наука, розвинулася з потреб практики. Вона виникла в середині ХХVІІ ст.. в зв’язку з задачами, які ставили страхова справа, демографія ( наука про народонаселення), теорія азартних ігор та ін..

У наш час значно зросла роль теорії ймовірності у житті. Сучасні природничо-математичні науки широко користуються теорією ймовірностей як теоретичною основою при обробці результатів спостережень у фізиці, механіці, астрономії, геодезії, біології, обчислювальній математиці. Теорію ймовірностей широко використовують в економіці, статистиці, військовій справі,  при виявленні оптимальних каналів зв’язку, на транспорті, у виробництві. У зв’язку з широким розвитком підприємств, що випускають масову продукцію, теорію ймовірностей використовують не лише для бракування продукції, але й для організації процесу виробництва (статистичний контроль на виробництві).[3]

Вона знайшла своє застосування у гуманітарних науках, зокрема в історичних дослідженнях в археології, при розшифруванні написів на мовах давно вимерлих народів.

Мета статті. Глибше розкрити основне поняття теорії ймовірностей - поняття подій.. На прикладах розв’язування задач  показати застосування комбінаторики до теорії ймовірностей.

Виклад основного матеріалу.                                                                        

Математики мають справу з подіями реального світу, що залежать від обставин, які або відомі, або не піддаються обліку. Наприклад, не можна  передбачити наперед, на який  білет випаде виграш у майбутньому тиражі, скільки зернин дасть певний колос від посіяної насінини, скільки випускників Львівських шкіл подадуть заяви на вступу до Львівського університету , чи будуть серед деталей, оброблених токарем за зміну, браковані. Такого характеру події називаються випадковими, а теорія ймовірностей займається вивченням масових  випадкових подій.

Важливим інструментом для вивчення ймовірності є комбінаторика.

Розглянемо три види сполук: розміщення, перестановки, комбінації.

Приклад 1.

Є 7 смужок пофарбованих у кольори спектра, тобто червона, оранжева, жовта, зелена, голуба,синя і фіолетова. Скільки можна з них виготовити різних прапорців: однокольорових, двокольорових, трикольорових і т.д.?

Розв’язання. Кількість кольорових прапорців дорівнює числу смужок, тобто , двоколірних - , триколірних -210,… шестиколірних , семиколірних .

Отже, ми знайшли кількість прапорців що відрізняються і кольорами смужок, і порядком їх розташування.

Приклад 2.

Перед випуском група учнів з 25 чоловік обмінялися фотокартками. Скільки всього було роздано фотографій?

Розв’язання. Передавання фотографій одним учнем другому є розміщення з 25 елементів по два елементи. Шукане число фотокарток рівне числу розміщень з 25 елементів по два елементи в кожному:

А=25·24=600.

Приклад 3.

Скільки чотиризначних чисел можна скласти з цифр 1, 2, 3, 4, 5 без повторень?                                                                                                              2

Розв’язання. За умовою дано множину з чотирьох елементів, які потрібно розташувати в певній послідовності. Отже, потрібно знайти кількість перестановок з чотирьох елементів:

Р_n=1·2·3·4·5=120.

Приклад 4.

Скількома способами можна розмістити 10 гостей на десяти місцях за святковим столом?

Розв’язання .Шукане число способів дорівнює числу перестановок із десяти елементів:

Р₁₀=10!=3628800.

Приклад 5.   

Монету підкидують два рази. Яка ймовірність того, що хоч один раз випаде герб?

Розв’язання. А₁ – два рази випав герб, А₂ – герб випав при першому киданні,

А₃ – герб випав при другому киданні, А₄ – герб ні разу не випав.

Р(А)=.

Приклад 6.

Набираючи номер телефону, абонент забув дві останні цифри, пам’ятав лише, що цифри різні, і тому набрав навгад. Яка ймовірність того, що набраний номер правильний?

Розв’язання. Дві останні цифри можна набрати способами, сприяє події тільки один спосіб. Тому Р(А)==.

Приклад 7.

Серед 100 електролампочок 5 зіпсутих. Яка ймовірність того, що вибрані навгад 3 лампочки будуть добрі?

Розв’язання. Зі 100 лампочок 3 лампи можна вибрати способами. Три добрих лампи  із загального числа 95 добрих ламп можна вибрати способами. Звідси, ймовірність дорівнює 

Р=.                                                                                     3

Приклад 8.

Скільки всього ігор мають провести 21 футбольна команда в одному чемпіонаті?

Розв’язання. Тому, що гра будь-якої команди А з командою В співпадає з грою команди В з командою А, то кожна гра є сполученням з 20 елементів по

2. Шукане число всіх ігор дорівнює числу сполучень з 20 елементів по 2 елементи в кожному:

С=

Приклад 9.

Скількома способами можна розділити 12 чоловік по групах, якщо в кожній групі 6 чоловік?

Розв’язання. Склад кожної групи є 6-елементною підмножиною множини з 12  елементів по 6 в кожному:

С

Ми вже згадували, що ймовірність є  поняття події, під якою розуміють будь-яке поняття, про яке можна говорити, що воно відбувається чи не відбувається. Причому, розглядаючи події, теорія ймовірностей цікавиться лише тим, відбувається чи не відбувається подія, абстрагуючись від конкретної природи самих подій.

Будь-яка подія відбувається внаслідок випробування(або досліду), тобто ті умови, в результаті яких відбувається подія.

Наприклад, підкидання монети – випробування, поява «герба» - подія, запитання вчителя – випробування, правильна відповідь учня – подія.

Випробування	Подія
Підкидання грального кубика     Гра в шахи     Випуск ламп електроламповим      заводом	Поява чотирьох очок Виграш у суперника Поява бракованої лампи

  Такі події є випадковими, бо вони можуть відбуватися або не відбуватися при здійсненні випробування.                                                                         4

Приклад 10.                                                                                                         

Гральну кістку кидають один раз. Яка ймовірність події: А – появи парного числа очок, В – появи не менше п’яти очок, С – появи не більше п’яти очок.

 Розв’язання. Дослід має шість рівно можливих незалежних наслідків ( поява одного, двох, трьох, чотирьох, п’яти і шести очок), які утворюють повну систему.

Події А сприяють три наслідки (випадання двох, чотирьох і шести очок) тому Р(В)=2/6=1/2; події В – два наслідки ( випадання п’яти і шести очок) тому Р(В)=2/6=1/3; події С – п’ять наслідків (випадання п’яти, одного, двох, трьох, чотирьох очок), тому Р(С)=5/6.

Приклад 11.

В урні лежать 7 червоних і 7 синіх кульок. З урни одночасно виймають дві кулі. Знайдіть ймовірність того, що обидві кулі червоні (подія А).

Розв’язання .Число рівноможливих незалежних наслідків дорівнює:

n=С. Події А сприяють m=С наслідків.

Отже, Р(А)=.

Приклад 12.

У партії з 24 деталей п’ять бракованих. З партії вибирають навмання 6 деталей. Знайдіть ймовірність того, що серед цих 6 деталей виявиться 2 браковані ( подія А).

Розв’язання. Число рівно можливих незалежних подій дорівнює n=С24!/(6!·18!)=134596.

Підрахуємо число наслідків, сприятливих для події В. Серед 6 взятих навмання деталей  повинно бути 2 браковані і 4 стандартні. Дві браковані деталі з п’яти можна вибрати С способами, а 4 стандартні деталі з 19 стандартних деталей можна вибрати  С способами.

Кожна комбінація бракованих деталей може сполучатись з кожною комбінацією стандартних деталей, тому m=3876·10=38760.                           5

Отже, Р(А)=38760/1345960,3.

Приклад 13.                                                                                                   

Дев”ять різних книг розташовані навмання на одній полиці. Знайти ймовірність того, що чотири книжки виявляться поставленими поряд

 (подія А).

Розв’язання .Тут число рівноможливих незалежних наслідків є n=Р₉=9!.

Уявимо собі, що чотири певних книги пов’язані разом, тоді цю зв’язку можна розташувати на полиці Р₆=6! способами (зв’язку додати до решти п’яти книг). В середині зв’язки чотири книги можна переставити Р₄=4! способами. При цьому кожна комбінація в середині зв’язки може сполучатись з кожним Р₆ з способів утворення зв’язки, тобто m=6!·4!. Отже, Р(А)= 6!·4!/ 9!=1/21.

У теорії ймовірності найчастіше доводиться обчислювати ймовірності складних подій, які складаються з сукупності простих фігур. Наприклад, при киданні двох гральних кубиків дістали в сумі 10 очок. Ця подія є складною, вона  може складатися з трьох простих подій:

1) на першому кубику випало чотири, на другому – 6 очок;

     2) на першому і на другому кубику випало по 5 очок,

     3) на першому кубику випало 6, а на другому – 4 очка.

   Обчислювати ймовірності складних подій за формулою Р(А)= буває важко, а інколи навіть неможливо. Їх імовірності  обчислюють через імовірності простих подій. Обчислення ймовірності складних подій через імовірності простих ґрунтується на застосуванні теорем додавання і множення. Дані теореми дають можливість найпростіше визначити шукану ймовірність подій, якщо безпосередній підрахунок усіх однаково можливих і сприятливих випадків або складний, або неможливий.

    Починаючи розв’язувати задачу, позначаємо подію, імовірність якої шукаємо, і події, імовірності яких відомі за умовою задачі. Спочатку доцільно перевірити, чи можна подати ймовірність шуканої події у вигляді суми або добутку подій, імовірністі яких відомі або легко знайти. Якщо це можливо, то шукану ймовірність обчислюють за допомогою теорем         6              додавання або множення. Якщо таке обчислення виконати не можна, то треба спробувати знайти шукану ймовірність через імовірність подій, протилежних даним. На практиці найчастіше буває, що потрібно застосовувати обидві теореми разом. При цьому подію, ймовірність якої шукаємо, подаємо у вигляді суми кількох несумісних подій. Обчисливши ймовірність кожного виду, можна, застосовуючи теорему додавання, обчислити шукану ймовірність.

Приклад 1.

Знайти суму подій: А - «поява одного очка при киданні гральної кості» і В -  «поява двох очок при киданні гральної кості».

Розв’язання Сумою А+В є подія С - «поява не більше двох очок при киданні гральної кості», тому А+В=С.

Приклад 2.

Знайти добуток подій А - «студент на екзамені витягує білет з парним номером» і В - «студент витягує білет з номером, який кратний п”яти».

Розв’язання. Добутком А·В є подія С - «студент витягнув білет з номером, який кратний десяти», тому А·В=С.

Приклад 3. Два стрільці стріляють незалежно один від одного по одній і тій самій цілі. При цьому ймовірність влучення для першого стрільця дорівнює 0,8, а для другого – 0,7. Визначити ймовірність влучення в ціль.

Розв’язання. Нехай А – влучання в ціль першого стрільця,  В – влучання другого, С -  влучання в ціль. Подію С можна подати у вигляді суми трьох несумісних видів подій цієї події С=А+В + АВ, де  А- подія, яка полягає в тому, що перший стрілець влучив у ціль, а другий промахнувся, В – другий влучив у ціль, перший промахнувся, АВ – обидва влучили.

Кожний з доданків є добутком двох незалежних подій, а тому для обчислення їх ймовірностей можна застосовувати теорему множення, а для обчислення імовірності події  С – теорему додавання:

Р(С)= Р(А) +Р(В) +Р(АВ) = Р(А)Р() + Р()Р(В) + Р(А)Р(В)= =0,8·0,3+0,2·0,7+0,8·0,7=0,24+0,14+0,56=0,94.                                                 7

 

Приклад 4.                                                                                                       

 В ящику лежать 20 деталей, причому 5 з них стандартні. Робітник бере 3 деталі. Знайти ймовірність того, що хоча б одна з них стандартна (подія А).

Розв’язання .Нехай В – подія, яка полягає в тому, що одна взята деталь стандартна, а дві – нестандартні; С – подія, яка полягає в тому, що дві взяті деталі стандартні, а одна – нестандартна; D – подія, яка полягає в тому, що всі три взяті деталі стандартні.

Очевидно, що подія А відбудеться, якщо відбудеться хоча б одна з подій В, С, D. Отже, подію А ми можемо записати як суму В, С, D. Події В, С, D несумісні, отже Р(А)=Р(В)+Р(С)+Р(D)= .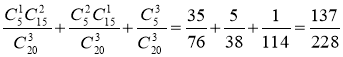

Дану задачу можна розв’язати простіше. Якщо ввести подію - жодна з взятих трьох деталей не буде стандартною.  Тоді Р(А)=1- Р(), а знайшовши ймовірність події

=. Обчислимо Р(А)=1-.

Приклад 5.

Із колоди в 36 карт навгад виймається одна. Чи є подія А ( поява туза) і подія В (карта червоної масті) незалежні?

Події А сприяють 4 елементарні події, тому Р(А)=. Якщо відбулася подія В, то це означає, що здійснилася одна з 18 елементарних подій, серед яких події А сприяють дві. Отже, Р=. Р(А)=Р, тобто події А і В незалежні.

Приклад 6.

Із колоди в 36 карт навгад виймається одна. Яка ймовірність того, що вийнята карта – піка або туз?

Подія А( піка) і подія В(туз) не є сумісні. Тому для обчислення ймовірності події АВ використовуємо формулу Р(АВ)=Р(А)+Р(В)-Р(АВ).      

                                                                                                                              8

Р(А)=, Р(В)=, Р(АВ)=. Р(АВ)=.

Приклад 7.

Знайти ймовірність того, що навмання вибране двоцифрове число буде кратним або 3, або 4, або обом зразу.

Розв’язання Нехай А – подія, яка полягає в тому, що вибране число кратне 3, а В – в тому, що вибране число кратне 4. Знайдемо Р(А+В). Оскільки А, В – сумісні події, то Р(А+В)= Р(А)+Р(В)-Р(АВ).

Обчислимо: Р(А)=30/90 ( серед чисел від 10 до 99 саме 30 кратні 3). Р(В)=22/90 (чисел кратних 4 серед двоцифрових 22). Знайдемо Р(АВ)=8/90 (числа 12, 24, 36, 48, 60, 72, 84, 96 кратні і 3 і 4), отже Р(А+В)=.

Приклад 8.

В ящику 12 деталей, серед них 8 бракованих. Робітник бере за один раз 2 деталі, а потім за другий раз ще 2 деталі. Яка ймовірність, що взяті  деталі  стандартні?

Розв’язання. Нехай подія А – полягає в тому, що перший раз взяті деталі стандартні; подія В – полягає в тому, що за другий  раз взяті деталі стандартні. Тому, що А, В – залежні події, то

Р(АВ)=Р(А)Р_А(В)=.

Приклад 9.

В одній урні 5 білих і 3 чорних куль, а у другій – 6 білих і 4 чорні кулі. Яка ймовірність, що з обох урн візьмуть білу кулю?

Розв’язання .Нехай А – подія, яка полягає в тому, що білу кулю взяли з першої урни; В – білу кулю взяли з другої урни. Тому, що події А, В – незалежні, то Р(АВ)=Р(А)Р(В)=.

Приклад 10.

Нехай деталі виготовляють на трьох верстатах. На першому виготовлено 40% всіх деталей, на другому - 35%, і на третьому - 25%. На першому 90%         9 деталей були 1 сорту, на другому 80%, і на третьому - 70%. Яка ймовірність, що взята деталь 1 сорту?

Розв’язання. Складемо гіпотези:

Н₁ – деталь виготовили на першому верстаті.

Н₂ -  деталь виготовили на другому верстаті.

Н₃ - деталь виготовили на третьому верстаті.

Подія А – взята деталь першого сорту, може відбутись одночасно з кожною з гіпотез  Н₁.

Тоді Р(А)=Р(Н₁)Р_Н1(А)+ Р(Н₂)Р_Н2(А)+ Р(Н₃)Р_Н3(А)

З умови задачі видно, що

Р(Н₁)=0,4                                      Р(Н₂)=0,35                                  Р(Н₃)=0,25

Р_Н1(А)=0,9                                    Р_Н2(А)=0,8                                  Р_Н3(А)=0,7.

Отже, Р(А)=0,815.

Р_Н1(А)= Р(Н₁)Р_Н1(А)/Р(А)=3/5.

Багато задач теорії ймовірностей зводиться до схеми, що називається схемою Бернуллі. [4]

Приклад 1.

Ймовірність влучення в ціль з одного пострілу 0,8. Яка ймовірність влучити в ціль 7 разів з 10 пострілів?

Розв’язання. Загальне число випробувань n=10, число k=7. Отже, ймовірність влучити 7 разів з 10 пострілів за формулою Бернуллі рівна:

Р₁₀(7)=(0,8)⁷(1-0,8)^10-7=(10!/7!3!)·(0,8)⁷(0,2)³=0,2.

Приклад 2.

В урні 20 куль: 15 білих і 5 чорних. З урни послідовно беруть 5 куль, причому кожну взяту кулю повертають в урну перед наступною спробою. Знайдіть ймовірність того, що з 5 куль 2 будуть білі.

Розв’язання. Ймовірність взяти білу кулю в кожній спробі рівна р=15/20=3/4, а чорну – q=1- р=1/4. За формулою Бернуллі знайдемо:

Р₅(2)=.

Приклад 3.                                                                                                        10

Проводяться 5 вистрілів, причому ймовірність попадання при кожному вистрілі 0,8. Яка ймовірність того, що в мішень попадуть 3 рази?

За формулою Я.Бернуллі, n=5, k=3, p=0,8, знаходимо

Р(3)=

Висновки. Практика свідчить, що використання елементів комбінаторики, активізація пізнавальної творчої діяльності, відкриває учням нові можливості застосування теорії ймовірності.

 

Література

1. А.Г.Мордкович. Алгебра і початки аналізу, 1979, ст..371-380.
2. А.Г.Цыпкин, А.И.Пинский. Справочное пособие по методам решений задач по математике для средней школы., 1984, ст.338-359.                 

                                                                                                                 12

3. Математика. Посібник для факультативних занять у 10 класі., 1970, ст.3-70.
4.  Р.О.Самойлова. Елементи теорії ймовірностей. Математика 2003, ст..12.
5.  Я.С.Бродський. Комбінаторика без формул. Знайомство з імовірністю та комбінаторикою. Математика в школах України. 2004. ст72-95.