Стаття «Формування та розвиток мотиваційних установок учнів до вивчення математики в умовах соціалізації особистості»

Криворізька загальноосвітня школа І-ІІІ ступенів № 8

Криворізької міської ради Дніпропетровської області

 

 

 

 

 

 

 

 

 

«

 

 

 

Невмержицька Тетяна Григорівна, вчитель математики Кваліфікаційна категорія «спеціаліст вищої категорії», вчитель-методист

 

 

 

 

 

 

 

 

 

 

 

 

 

Кривий Ріг

2019

 

 

 «Формування та розвиток мотиваційних установок учнів до вивчення

математики в умовах соціалізації особистості»

 

Педагогічне кредо: «Справжній учитель той, хто здатний спуститися з висот своїх знань до незнання учня і разом з ним здійснити сходження».

 

ПРИТЧА ПРО МОТИВАЦІЮ

         Чернець, який керував будівництвом собору, вирішив подивитися, як працюють каменярі.  Він підійшов до першого і попросив його розповісти про свою роботу.

        - Я сиджу перед кам'яною брилою і працюю різцем. Нудна і виснажлива робота, - сказав той зі злістю.

        Чернець підійшов до другого муляра  і поставив йому те ж питання.

        - Я ріжу камінь і заробляю цим гроші. Тепер моя сім'я не голодує, - стримано відповів другий муляр.

        Чернець запитав і третього каменяра про його роботу.

        - З боку здається, що я ріжу камінь. Але насправді я ьудую Храм, який простоїть тисячу років. Я будую майбутнє, - посміхнувшись, відповів муляр.

         На наступний день чернець запропонував третьому каменяреві очолити будівництво храму.

 

ОСНОВНІ ПРОБЛЕМИ, НАД ЯКИМИ ПРАЦЮЮ:

1. Формування стійких мотиваційних установок до вивчення математики на основі підвищення практичної значущості математичних знань.

2. Розвиток математичної компетентності учнів за допомогою сучасних інтерактивних технологій та міжпредметних зв'язків на основі компетентнісно орієнтованого підходу.

3. Створення умов для формування і розвитку життєтворчих компетенцій і продуктивної творчої діяльності

4. Впровадження моніторингу навчальної діяльності учнів як способу корекції успішності і розвитку навчальних компетенцій учнів.

 

          СУТНІСТЬ ДОСВІДУ: створення умов для формування і розвитку позитивних установок на засвоєння математичних знань при поглибленні практичної спрямованості змісту уроку.

 

        АКТУАЛЬНІСТЬ ДОСВІДУ: Національною доктриною розвитку освіти виділено основне завдання - створення умов для розвитку особистості і творчої самореалізації кожного громадянина України, виховання покоління людей, здатних ефективно працювати і навчатися протягом усього життя. Проблемою сьогоднішнього дня є зниження інтересу до математики у більшості дітей, і як наслідок, рівня її засвоєння, в силу відсутності стійких особистісно-значущих мотивів, які працюють на перспективу. Разом з тим сучасна людина без математичної освіти обійтися не може, тому що математичну освіту - це єдине минуле випробування часом засіб інтелектуального розвитку; елементи математики - невід'ємна частина загальної системи орієнтації в навколишньому світі; математика має колосальний виховним потенціалом. Тому формування стійких мотиваційних установок до використання математичних знань у всіх сферах діяльності і повсякденному житті є об'єктивною необхідністю.

          В основі моєї роботи лежать педагогічні ідеї видатних педагогів Я. А. Коменського, К. Д. Ушинського, В. О. Сухомлинського, загальна ідея яких полягає в тому, що для успішного навчання необхідно розвиток творчості учня. Використано елементи технологій: теорії особистості як суб'єкта діяльності (Б. Г. Ананьєв, О. М. Леонтьєв, Л. С. Виготський.), проблемного навчання математики в 5-11 класах (автори Дж. Дьюї, А.М.Матюшкин і ін.); розвиваючого навчання (Д.Б. Ельконін, В. В. Давидов); інформаційних і здоров'язберігаючих технологій. Цікавою і близькою до мого досвіду вважаю теорію розвитку пізнавальних інтересів Г. І. Щукіна та теорію активізації навчальної діяльності школяра А.К. Маркової.

 

         

ТЕХНОЛОГІЯ ДОСВІДУ

          «У навчанні, щоб не формально засвоїти матеріал, треба не пробути, а прожити навчання, треба, щоб навчання увійшло в життя дитини, щоб воно мало для нього особистісний сенс».

                                                                                                 А.Н.Леонтьев

 

             Працюючи над даною проблемою, мною були визначені наступні напрями педагогічної діяльності:

            1.Удосконалення змісту математичної освіти шляхом насичення його прикладними і сюжетними завданнями;

            2.Використання ігрових технологій на уроках математики;

            3.Проведення нестандартних уроків, заснованих на матеріалах громадського, економічного, регіонального компонента, історичного та екологічного змістів;

            4.Впровадження в навчання інформаційних, комп'ютерних та здоров'язберігаючих технологій.

            5. Залучення учнів до активної позакласної роботи з предмета.

  Завдання, яке стоїть переді мною, - подолання формальності у викладанні математики. Головний шлях її вирішення - зміцнення зв'язку навчання з життям, з практикою, тому що всі значні явища життя, що стали звичними для дитини в силу своєї повторюваності, можуть і повинні придбати для нього в навчанні несподівано нове, повне сенсу, зовсім іншого звучання. І це обов'язково буде стимулом мотивації учня до пізнання.

Реалізацію цієї проблеми здійснюю, перш за все, через зміст завдань - прикладних і сюжетних, які викликають у учнів непідробний інтерес (додаток 1). При вирішенні таких завдань учні знайомляться з важливими в пізнавальному і виховному відношенні фактами. Так, рішення задач, що містять відомості про здоровий спосіб життя і засновані на фактичному матеріалі, змушує по-новому поглянути на цю проблему, закликають дітей цінувати, поважати і берегти своє здоров'я. Цікавими і пізнавальними для учнів є сюжетні завдання на основі матеріалів про «Шерлок Холмс йде по сліду» (додаток 2) та «Ігри на уроках математики » (додаток 3), які я використовую у своїй практиці.

Таким чином, фактичний зміст завдань сприяє створенню зовнішньої і формуванню стійкої внутрішньої мотивації до вивчення математики, що в кінцевому підсумку формує життєтворчі компетентності учнів.

Поєднання прикладних задач, які використовуються на уроці, з творчими домашніми завданнями, складанням і оформленням тематичних альбомів і альманахів сприяє залученню школярів до людської культури в цілому, розвитку творчих можливостей учнів, усвідомлення і більш глибокому засвоєнню програмного матеріалу основного курсу математики на рівні практичного застосування знань, умінь, навичок в нових умовах. Так, з учнями 5-х класів були підготовлені альманахи за напрямками: мої батьки, спорт, здоров'я, природа і т.д. (Додаток 4). Використання такого матеріалу в навчанні математики дозволяє побачити «живу математику», а не «суху бездушну науку».

Людина формується в процесі активної діяльності і, чим вона різноманітніше, тим різнобічне його особистість. А.С. Макаренко, великий поборник дитячої гри, писав: «Який дитина в грі, такий багато в чому він буде в роботі, коли виросте». Я цілком солідарна з ним. Гра, спілкування, навчання, праця - ось основні ступені сходження особистості до успіху. Тому в своїй роботі я часто використовую ігрові технології на різних етапах уроку: при перевірці домашнього завдання, при закріпленні пройденого матеріалу, при повторенні. Це і рольові ігри, і розгадування кросвордів, шифрограму, ребусів, математичних загадок, і інсценування, і математичне лото, і бліцтурнірі, і вікторини (додаток 5).

Для створення зовнішньої і підтримки стійкої внутрішньої мотивацій учнів велике значення мають нестандартні уроки, спрямовані на продуктивну творчу діяльність дітей. З цією метою розроблена система нестандартних різновекторних уроків: подорожей, експедицій, досліджень, «лицарські турніри» і т.п. (Додаток 6). На таких уроку діти вживаються в роль геологів, туристів, реставраторів, дослідників, залучаються до гри і з легкістю вирішують серйозні завдання, домагаючись поставленої мети, що сприяє розвитку мотивації.

Освітній процес на уроці спрямований на збереження здоров'я учнів, тому що це основа самореалізації особистості в майбутньому. Вирішення цього завдання - використання здоров'язберігаючих технологій. Тому, вважаю за необхідне використання такого технологічного елементу як динамічні паузи або психологічні релаксації на кожному уроці. Особливо дітей залучають фізкультхвилинки в віршах або хвилинки, коли включається уява хлопців (додаток 7). При підборі фізкультхвилинок та динамічних пауз намагаюся, щоб вони органічно впліталися в канву уроку. Витрачений час окупається посиленням працездатності, а головне, зміцненням здоров'я учнів.

Використання ІКТ дозволяє на уроці зробити складну науку математику більш доступною для розвитку творчих здібностей учнів. Система роботи з ІКТ в даний момент включає:

• робота в мережі Інтернет; з власним сайтом (адреса сайту: http://uchitmatematika.ucoz.ru);

• залучення учнів до пошуку фактичних матеріалів в мережі Інтернет для міні-досліджень і творчих завдань;

• електронні презентації з різних тем:   «Математика здоров'я у відсотках» (5 клас).

• створення особистого банку по розділах: «Поурочні плани», «Класне керівництво», «Позакласна робота», «Портфоліо класу».

Використання можливостей комп'ютера на уроках математики доставляє щире задоволення і захоплення мені, як вчителю, і моїм допитливим учням. Багатогранні уроки, наповнені особистісно-цінних для дітей змістом долучають їх до творчості та пізнання, тим самим переводячи освітній процес на більш високий рівень.

Математиками стане лише невелика частина моїх учнів. Переважна більшість вибере професії, не пов'язані тісно з «царицею наук». Що дасть математика їх майбутньої професії? У чому вже зараз допомагає математика в їх повсякденному житті і навчанні? Ось на ці питання намагаюся дати відповідь кожному школяреві, щоб він бачив живу і безпосередній зв'язок математичних методів з завданнями, які ставить перед школярами життя.

 

 

 

 

 

 

 

 

 

 

Додаток 1

Завдання прикладного характеру

 

1. Екологія

1) Кинута на землю шкірка банана в нашому кліматі розкладається близько 2 років. Кинутий недопалок сигарети розкладається на 2 роки довше. Пластиковий пакет розкладається на 8 років довше, ніж недопалок сигарети. Скільки років потрібно для того, щоб розклався пакет? На скільки років раніше розкладеться шкірка від банана?

2) Дерева сприяють очищенню повітря від пилу і інших забруднень. Листяний ліс, площа якого дорівнює площі квадрата зі стороною 100 м, може протягом року затримати 68 т пилу. Зате ялиновий ліс такий же площі здатний за той же час затримати 32 т пилу. На скільки тонн пилу більше затримує листяний ліс, ніж ялиновий?

3) Кожна автомашина викидає в атмосферу в 3 рази більше забруднюючих речовин в порівнянні зі своєю власною масою. Маса вантажівки 3 тонни. Яка кількість забруднюючих речовин викидає в атмосферу така машина?

4) Один погано закритий кран призводить до втрати 20 л води за добу. У школі діти залишили погано закрученими 4 крана. Скільки води було витрачено протягом доби?

5) На виробництво 1 т паперу потрібно 17 дерев. Кожна тонна макулатури рятує ці дерева від вирубки. Скільки потрібно зібрати макулатури, щоб зберегти 51 дерево?

6) 100 дерев ялинового бору затримують 3 т шкідливого пилу протягом року, а 100 дерев букового лісу - 7 т пилу. Який з двох типів лісу затримує більшу кількість пилу: 100 дерев ялинового лісу або 50 дерев букового лісу?

 

2.Сім  чудес України

1) У парку «Софіївка» виростає 2103 виду деревних рослин, що на 891 більше, ніж трав'янистих. Скільки всього видів рослин росте в парку?

2) Фортеця Кам'янець Подільського має форму прямокутника. Його ширина 56 метрів, що в 4 рази менше його довжини. Який шлях нам доведеться пройти, щоб обійти фортецю?

3) Довжина Софійського собору без галерей 29м, ширина-28; з галереями: довжина-55м, ширина-42м. На скільки площа собору з галереями більше площі собору без галерей?

4) Визначимо площу і протяжність острова Хортиця, що має форму прямокутника, довжина якого дорівнює 12,5 км, а ширина 2,5 км.

 

3.Здоров’я

1) У тютюновому димі однієї сигарети міститься багато отруйних речовин, що руйнують організм. Визначте процентний вміст самих отруйних речовин - синильної кислоти, тютюнового дьогтю, окису вуглецю, полонію, - в одній сигареті, якщо нікотину 2%, а синильна кислота становить частину нікотину; тютюнового дьогтю в 7,5 раз більше, ніж нікотину; окис вуглецю становить від кількості тютюнового дьогтю, полоній 210 ​​становить від кількості окису вуглецю.

2) Одна сигарета руйнує 25 мг вітаміну С. Денна норма прийому вітаміну С 500 мг. Скільки вітаміну краде у себе той, хто викурює 14 сигарет в день? Скільки вітаміну С у нього залишається?

3) Вміст вітаміну В₆ в 100 г квасолі 0,9 мг, що становить 52% від добової норми для підлітків. Знайти добову норму вітаміну В₆. Відповідь округли до десятих. Скільки потрібно з'їсти квасолі для задоволення добової потреби у вітаміні В₆?

 

                                                                                                    Додаток 2

 

Учитель: В общей сложности Шерлок Холмс появляется в 56 рассказах и 4 романах Артура Конан-Дойля. В большинстве случаев повествование ведётся от имени друга и спутника Холмса — доктора Ватсона. Первая книга о знаменитом детективе -  роман «Этюд в багровых тонах», написана Артуром Конан-Дойлем в 1887 году. Последний сборник «Архив Шерлока Холмса» опубликован в 1927 году.

 

Биография и место проживания

 

Приблизительно год рождения Холмса 1854. Таким образом: в 1881 году Холмс знакомится с доктором Джоном Ватсоном. Холмсу около 27 лет. Он, по всей видимости, небогат, так как ищет компаньона для совместного съема квартиры. Тогда же они с Ватсоном переезжают на Бейкер-стрит, 221-б (Baker Street 221 B) где долгие годы совместно снимают квартиру у миссис Хадсон. На самом деле дома с таким номером на реальной Бейкер стрит никогда не было. В настоящее время по адресу Бейкер-стрит, 221-б, находится музей Шерлока Холмса. Когда дом появился, на этот адрес обрушился поток писем. Одна из комнат этого здания считается комнатой великого сыщика. В фирме, расположенной по этому адресу, существует должность сотрудника для обработки писем Шерлоку Холмсу.

Холмс — многогранная личность. Одновременно талантливый скрипач, хороший боксер, искусный актёр, химик, он посвятил свою жизнь карьере частного детектива. Расследуя дела, которыми снабжают его клиенты, он опирается не столько на букву закона, сколько на свои жизненные принципы, правила чести, которые заменяют ему параграфы бюрократических норм. Неоднократно Холмс позволял людям, по его мнению, оправданно совершавшим преступление, избежать наказания. За свой труд по раскрытию преступлений Шерлок Холмс берёт справедливое вознаграждение, но если его очередной клиент беден, может взять плату символически.

Холмс не тщеславен, его не интересует благодарность за раскрытое преступление.               Сегодня  мы с вами отправимся в гости к знаменитому сыщику.

         (До начала урока учащиеся  делятся на две команды.)

Необходимое оборудование: мультимедийная установка, оценочный лист для жюри, карточки с буквами, каждому ученику выдаётся блокнот и ручка для вычислений.

Холмс: (сидя на стуле с газетой и куря трубку) Давненько я, Ватсон, не распутывал дел! Но вот сегодня мне принесли письмо от  директора школы! Мне стало интересно, что же она мне пишет! Представляешь, у нее  пропал пароль от главного компьютера! Теперь не сможет работать АС «Школа» и выпускники не смогут зарегистрироваться для прохождения внешнего тестирования!

Ватсон: Холмс! Неужели вам мало ваших старых похождений? Да и я за свою нелёгкую жизнь уже порядочно набегался и …

Холмс: Послушайте! Вот вы, например,   хотите узнать свою оценку по математике в детстве?

Ватсон: Да!

Холмс: А пользоваться благами , которые дает Интернет?

Ватсон: А кто ж не хочет…

Холмс: А вы представьте себя на месте тех детей, которые останутся без этого! Я чувствую мне нужно сменить мой домашний халат на выходной сюртук и разобраться в чём тут дело!

Ватсон: И как же вы хотите помочь нашему директору?

Холмс: Элементарно Ватсон! Сейчас посмотрим что дальше написано в письме! (громко читает): Оказывается, директор помнит, что   пароль был зашифрован в 6 задачах, которые приложены к письму! Отгадывая каждую из них, мы будем узнавать по букве из пароля! Но я уже не так умён на старости лет! Мои дедуктивные методы устарели…..

Ватсон: Быть может дамы и джентельмены, сидящие в классе, помогут нам в этом?...

 

                                                                                                     Додаток 3

 

Ігри на уроках математики

МАТЕМАТИЧНЕ ЛОТО за  темою  «НАТУРАЛЬНІ ЧИСЛА»

Правила гри:

1. Для гри вчителю слід підготувати два варіанти карток для лото загальною кількістю по числу учнів в класі.

2. Робота проводиться за варіантами.

3. Два учні (по одному від кожного варіанту) викликаються до дошки, інші працюють в зошитах.

4. Учитель зачитує питання, на кожен з яких відводиться 30 секунд. Учні закреслюють ті клітини в картках, числа в яких є, на їхню думку, відповідями на запитання вчителя. Слід пам'ятати, що в картці для гри може і не бути всіх правильних відповідей.

5. Взаємоперевірка проводиться в парах, звіряючись з дошкою.

6. Максимальна оцінка за всі правильні відповіді - 12 балів.

7. Учитель підводить підсумки за результатами лото і звертає увагу на помилки. Оцінки виставляються за бажанням учнів.

Вид карток для гри

I варіант

1	0	999		100
	20		10	14
101	7	16		13

 

II варіант

98	100		7	22
	13	16		20
999	0	1	10

 

Запитання для лото:

1. Яке з чисел натурального ряду є найменшим?

2. Згадайте казку про вовка і козенята. Скільки було козенят?

3. Яка з двозначних натуральних чисел є найменшим?

4. Яке число слід за найбільшим двозначним числом?

5. Яке число передує 1000 ?

6. Якщо а дорівнює 15, то чому дорівнює а + 1?

7. Якщо а дорівнює 21, то чому дорівнює а-1?

8. За приказками, яке число є нещасливим?

Відповіді:

У I варіанта повинні залишитися клітини з числами 0, 14, 101, у II - 0, 22, 98.

МАТЕМАТИЧНЕ ЛОТО за  темою «ВЕЛИЧИНИ»

Учням роздається картки-лото в декількох варіантах. Учитель читає завдання, а учні закривають вірні відповіді.

Запитання для лото:

1.v = 10 м / с, t = 5 с, s =?

2.v = 5 км / год, s = 15 км, t =?

3.а = 6 см, b = 20 см, S =?

4.а = 4 см, b = 3 см, P =?

5.11м 4дм-3м 7дм =?

6.2т 20кг · 7 =?

50 м		7 м 70 см
15 т 4 ц	3 ч
20 га	120 кв. см	14 см

Якщо учні правильно впоралися із завданням, то на картках повинно залишитися незакритим число 20 га.

 

МАТЕМАТИЧНЕ ЛОТО за темою «ЗВИЧАЙНІ ДРОБІ»

Вид карток для гри:

I варіант

7	24		8/9	7/6
13/14		3 2/10	<	3
	16	91	Да	6 1/4

( Якщо учень зробив все правильно,  то не закресленими повинні залишитися такі  записи: 24; 7/6; 13/14; <; 91) .

 

Да	45	6 1/4	36	3
>	8/9	3 2/10	6/6	1
Нет	13	7	16	11

ІІ варіант

(Якщо учень зробив все вірно, що не закресленими повинні залишитися такі записи: 36; немає; 11.)

Питання для лото:

1. Чисельник дробу 7/11.

2. Знаменник дробу 91/45.

3. Найбільша правильна дріб зі знаменником 9.

4. Найменша неправильна дріб зі знаменником 6.

5. Вирішіть нерівність в натуральних числах

                       1 <x / 15 <17/15

6. Порівняйте дроби 10/7 і 10/9 (знайдіть в картках знак «<» або «>»).

7. Розв'яжіть рівняння: а / 14 = 13/14.

8. Виділіть цілу частину з дробу: 25/4 =?

9. Яке ціле число записано дробом 36/12?

10. Знайдіть число, записане дробом 32/10.

11. Чи вірно рівність 32/32 = 5/5? ("Так чи ні".)

12. 24/24 =?

Вірні відповіді:

1) 7; 2) 45; 3) 8/9; 4) 6/6; 5) 16; 6)>; 7) 13; 8) 6 ¼; 9) 3; 10) 3 2/10; 11) Так; 12) 1.

ГРА «РЕСТАВРАТОР»

Якнайшвидше поставте замість "сніжинки" один із знаків: "=", "+", "-", "<", ">", щоб рішення задачі було вірним.

                          36 * 5 * 21 136 * 54 + 236

                          3х4 * 17 = 29 81 * 13 = 81 * 13

                          23 + 8 * 31- 9 400 * 313 + 87

                          14 * 4 = 10 72 = 144 * 72

                          6 * 8 * 4 = 10 9х8 * 16: 4

                          100 + 13 * 96 * 17 96: 6 * 4х4

 

ГРА «ЗНАЙДИ ПОМИЛКУ»

 

Дикобраз в подарунок синові

Зробив лічильну машину,

На жаль, вона

Недостатньо точна.

Результати перед вами,

Швидко все виправте самі:

 

 

39,4 + 10,1 = 4954;                      97,3 + 9,04 = 10,634;

 

47,03 + 4,8 = 5183;                      729,004 + 10 = 729,014;

 

3,067 + 2,033 = 51;                      31,26 + 0 = 312,6.

 

Знайдіть і виправте помилки.

До дошки в порядку черги виходять представники кожної з команд: одна пара гравців на одне завдання. Інші учні спостерігають за ходом виконання завдання.

Варіант 1:

1) 5 * 321 * 20> 4 * 322 * 25

2) 50 * 72 * 2 <5 * 4 * 3 * 2 * 9 * 5

3) 125 * 91 * 8 = 200 * 90 * 5

Варіант 2:

1) 25 * 186 * 4 <20 * 185 * 5

2) 5 * 4 * 6 * 7 * 1 * 5 * 2> 20 * 9 * 9 * 5

3) 20 * 50 * 78 = 125 * 87 * 8

 

 ГРА «ШУКАЙ ФІГУРИ»

 

Визначте, скільки  трикутників ви бачите  на рис.1 і квадратів на рис.2а, б

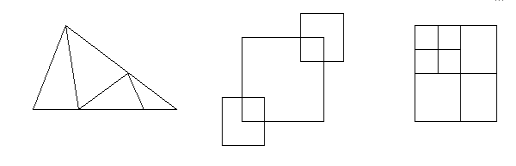
Рис.1     Рис.2а   Рис.2б

Відповідь: 7             Відповідь: 5  Відповідь: 9

 

Скільки трикутників на кожному рисунку?

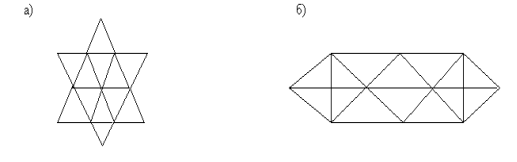
 Відповідь: 20     Відповідь: 28 

 

 

 ГРА «ЯКЕ  ЧИСЛО ЗАЙВЕ?»

1.       ;   ;   2;   ;        (Зайвим є число 2, т.я. воно натуральне, а всі інші – дробові).

 

2.     ;    ;    ;    ;    ;         (Зайве число  , т.я. це неправильний дріб, і він більше 1).

 

3.     ;    ;    ;    ;    ;          (Зайве число    , т.я.  це правильний дріб, і він меньше 1).

 

 

                                                                                                            Додаток 4

Розробка позакласного заходу з математики  

"Свято математики". 6-й клас

Цели:

•                   развитие логического мышления, внимания, интереса к предмету;
•                   формирование навыков общения, умения работать в коллективе.

Ход игры

Сегодня с нами те, кто хочет учиться с увлечением, все, кто любит тайны, загадки, приключения, кто любознателен, трудолюбив, настойчив. Дорогие участники игры, захватите с собой смекалку, находчивость, смелость, а смелость, говорят, города берёт, и тогда победа будет за вами. Успехов вам!

Разыграем порядок выхода команд (1 и 2). Жюри оценивает выступление команд по 5-бальной системе.

Визитная карточка 1 команды. Затем визитная карточка 2 команды.

Жюри подводит итоги.

Команды готовы к игре?

Болельщики готовы к игре?

Начинаем 1 конкурс. “Знаете ли вы великих математиков?”.

Для подсказки: вопросы по биографии Пифагора, Архимеда, Карла Фридриха Гаусса.

Вопросы задаются вслух, каждая команда записывает свои варианты ответов. После того как результаты сданы, заслушать верные ответы.

1). Кто из математиков древности погиб от меча римского солдата, гордо воскликнув: “Отойди, не трогай моих чертежей!”? (Архимед).

2). Вся его жизнь легенда. Он родился на острове Самос, у берегов Малой Азии. В зрелом возрасте переселился в Сицилию и создал свою школу, одной из заповедей которой была: не делай никогда того, что не знаешь, но научись всему, что следует знать. (Пифагор).

3). Какой учёный помог победить римский флот близ Сиракуз с помощью “зажигательных вогнутых зеркал”. (Архимед).

4). Какой великий математик завещал начертать правильный 17- угольник, вписанный в круг, на своей надгробной доске. (Гаусс).

5). Кто является автором многих изобретений, например, машины для орошения полей и рычагов, блоков и винтов для подъёма больших грузов. (Архимед).

Следующий конкурс. “Математический ералаш”.

Предмет “математика” настолько серьёзен, что полезно не упускать 
возможности сделать его более занимательным.

Блез Паскаль.

Учить можно только весело. . .
Чтобы переваривать знания, надо поглощать их с аппетитом.

Анатоль Франс.

Именно этими девизами мы будем пользоваться при проведении следующего этапа соревнований. Понятно, что речь идёт не о веселье в прямом смысле, а о чувстве удовлетворения, которое возникает в процессе обучения.

Даётся минута, за которую надо составить как можно больше математических терминов, слов, связанных с математикой, в единственном числе, именительном падеже.

Итак, буква П. Время пошло!

Параллелепипед, параллельность, перпендикулярность, последовательность, прямая, призма, прямоугольник, параллелограмм, пять, плюс, пирамида…

Болельщики составляют самое длинное слово на П (последовательность).

Теперь слово АРИФМЕТИКА. Время пошло! Рифма, метка, тик, кит, рама, Рим, фетр, риф, ар, рак, тема, река, материк, фирма... Время истекло!

Жюри подводит итоги.

Следующий конкурс: “Решение занимательных задач”.

Расшифруйте 2 ребуса, в которых одинаковым буквам соответствуют одинаковые цифры, а разным буквам – разные цифры в обоих примерах.

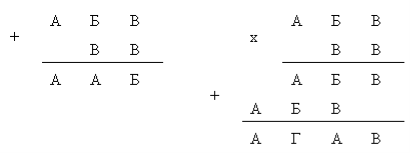
Разместите 8 козлят и 9 гусей в 5-ти хлевах так, чтобы в каждом хлеве были и козлята и гуси, а число их ног равнялось 10.

У Гарри Потера есть волшебные очки, в которых он видит всё зелёное – белым, а всё белое – зелёным. Гарри посмотрел через эти очки на прямоугольник. Что он увидел?

 

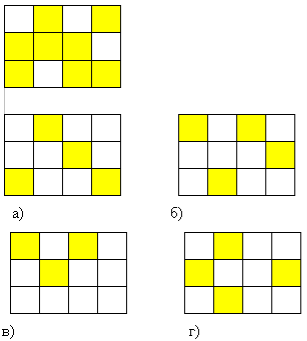
Чтобы открыть секретную дверь в пещеру гномов, нужно заполнить четырьмя магическими знаками таблицу 4х4. В каждой строчке и в каждом столбце должен встречаться каждый из знаков. Маленький гномик начал заполнять эту таблицу. Какой из знаков должен быть в клеточке с “?”.

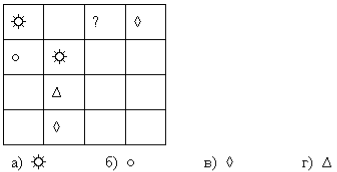
Мальчик сложил квадратный листок бумаги пополам, потом ещё раз и ещё раз. В центре то, что получилось, он проделал дырку, а потом снова развернул лист. Сколько дырок он увидел?

а) 2

б) 3

в) 4

г) 6

д) 8

Болельщики в это время тоже решают задачки.

1). Какая из букв слова КЕНГУРУ имеет самый большой порядковый номер и какой? (У - 21).

2). У близнецов Бори и Вовы есть 2 грязных носа и 4 грязных щеки. Сколько чистых носов и щёк окажется у 2 близнецов, если половину грязных носов и щёк вымыть с мылом? (1 чистый нос и 2 чистые щеки).

3). Боре и Вове купили 2 пары ботинок. Боря потерял свой левый ботинок, а Вова – правый. Сколько пар ботинок осталось после этого у близнецов? (1 пара).

4). У Бори и Вовы было 5 котлет. Сколько котлет осталось у близнецов после того, как одну котлету они разделили пополам и метко кинули 2 разным собакам, 3 котлеты нечаянно уронили с балкона на одного итого же прохожего? (1 котлета).

5). Близнецы Боря и Вова рисовали одну картину и перемазались красками. Боря вымазался 3 красками – красной, зелёной и чёрной, а Вова 2 красками – белой и красной. Сколько разных красок можно насчитать на близнецах? (4 краски)

6). У Бори и Вовы 1 мяч и 4 ноги. Сколько раз били близнецы по мячу ногами и промахивались, если известно, что каждый близнец 2 раза промахнулся по мячу каждой ногой. (8 раз).

За каждый первый верный ответ – приз.

Жюри подводит итоги.

Новый конкурс. “Что мы знаем о числах?”

Современные люди широко применяют в своей жизни числа. Вряд ли кто-нибудь сейчас вкладывает в числа сказочный или мифический смысл. Но так было не всегда. Для древних людей числа были элементами особого кода, с помощью которого описывался мир человека. В наиболее древних текстах число “1” встречается крайне редко и означает единство. Число “1” приписывалось Богу и Космосу.

Число “2” лежало в основе противопоставлений, с помощью которых в некоторых мифах описывался мир. Например, Небо и Земля, День и Ночь, Жизнь и Смерть.

В любых древних культурах одно из наиболее употребляемых чисел – “12”. Оно оставило яркий след в современной культуре. Это 12 месяцев, 12 часов. Число “12”, как и “7” считается счастливым.

Ему противостоит “несчастливое” число “13”. Это число называют “чертова дюжина”. Многие суеверные люди и сейчас остерегаются этого числа.

Командам было дано задание приготовить рассказ о каком-либо числе. Сообщения команд.

Последний конкурс в соревновании. “Пословицы и поговорки с числами”.

Команды называют по одной пословице (или поговорке) с заданным числом. Побеждает та команда, которая последней назовёт пословицу. Используются числа 1, 5, 7, 10.

Жюри  подводит  итоги.

Праздник закончен. Итоги подведены. Все члены команд получают призы. Призы получают и наиболее активные участники из зрителей, которые принимали участие в подготовке.

 

                                                                                                                    Додаток 5

КРОСВОРД   «ЮНИЙ МАТЕМАТИК»

 

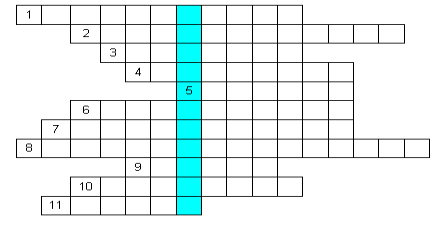
Питання:

1.Числа, що вживаються при рахунку предметів. (Натуральні)

2.Чотирикутник з прямими кутами. (Прямокутник)

3.Цифри 0, 1, 2, 3 ... (Арабські)

4.Наглядне уявлення різних числових даних. (Діаграма)

5.Результат від ділення. (Частка)

6.Число, що показує, на скільки рівних частин поділено ціле.

  (Знаменник)

7.Сумма однакових доданків. (Добуток)

8.Закон складання. (Переставний)

9.Площа  квадрата зі стороною 100 м. (Гектар)

10.Відрізок, довжина якого дорівнює 1. (Одиничний)

11.Кут менше прямого. (Гострий)

Ключове слово: Лобачевський

 

 

    РЕБУСИ

                                                                                                                                                                  Родина                                                                                

          Лінійка

 

 

 

       

                                                                                  

                                                                          Точка     

 

Один

                  

                                                      Дробь

                              

   Задача

                  

                      Вектор  

                 

 

 

 

              Знак                                                      

                                                                                        

                                                                                                               Мінус

 

 

            

 

                 П’ять                             

 

 

 

                                                                                

                                                                                                                             

                            

                                                         Степень                      

                                                                                                              

         Вершина         

 

 

 

   

 

 Додаток 6

 

Нестандартні уроки математики

 

Клас	Тема уроку	Тип уроку	Технологія проведення
5	Натуральні числа	Урок узагальнення знань	Подорож в минуле  «Число та містика»
5	Додавання і віднімання натуральних чисел	Урок узагальнення знань	«Ключі від форту Математики»
5	Множення і ділення натуральних чисел	Урок узагальнення знань	Урок-гра «Хрестики - нулики»
5	Геометричні фігури	Урок узагальнення знань	Урок-пригода «В царстві Математики»
5	Додавання і віднімання десяткових дробів	Урок узагальнення знань	Подорож «Морські пригоди»
5	Множення десяткових дробів	Урок узагальнення знань	«Десяткові дроби в Мумі-домі»
6	Додавання і віднімання дробів з різними знаменниками	Урок закріплення знань	Математична гра «Шерлок Холмс йде по сліду»
6	Відношення і пропорція	Урок узагальнення знань	«Золотий переріз в архітектурі, живописі та музиці»
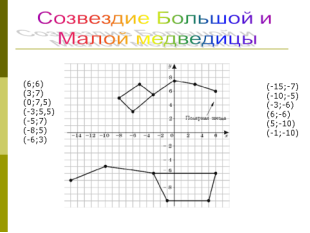
6	Координатна площина	Урок узагальнення знань	Подорож по зоряному небі «Знаки Зодіака»
6	Площа круга	Урок закріплення знань	«День народження числа π»
7	Многочлени	Урок закріплення знань	«Компанія «Удача». Розв’яжемо будь-яку задачу з многочленами»
7	Трикутники	Урок узагальнення знань	«Чудові точки трикутника»
8	Чотирикутники	Урок узагальнення знань	«Геометричне перетворення простору»
8	Квадратні корені	Урок узагальнення знань	Подорож  множиною дійсних чисел

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток 7

 

 

Гімнастика для очей

 

***

Філін. Учням пропонується закрити очі і тримати їх закритими 3-4 секунди. Широко розкрити очі, дивитися вдалину і не моргати протягом 5-6 секунд.

 

***

Малювання носом. Дітям потрібно подивитися на табличку і запам'ятати слово або букву. Потім закрити очі. Уявити собі, що ніс став таким довгим, що дістає до таблички. Потрібно написати своїм носом обраний елемент. Відкрити очі, подивитися на табличку. (Учитель може конкретизувати завдання відповідно до теми уроку.)

***

Далеко - близько. Вправа проводиться вчителем, який називає спочатку віддалений предмет, а через 2-3 секунди - предмет, розташований близько. Учням необхідно швидко відшукати предмети, які називає учитель