Стаття "Розвиток предметних компетентностей здобувачів освіти засобами застосування прийому «свято однієї задачі» при розв’язанні ірраціональних рівнянь"

Розвиток предметних компетентностей здобувачів освіти

засобами застосування прийому «свято однієї задачі»

при розв’язанні ірраціональних рівнянь

             Важливу роль у розвитку творчих здібностей здобувачів освіти, які покладено в основу компетентнісного підходу при вивченні алгебри та початків аналізу, формуванні предметних компетентностей під час освітнього процесу відіграє урок - свято однієї задачі. Ключове завдання алгебри – не просто розв’язання рівнянь різного виду, типу та  рівня складності – а формування практичних прийомів добору оптимального способу їх розв’язання.  Тому мета проведення такого уроку – не лише розв’язати одну задачу (рівняння) різними способами, а й формування навичок аналізу умови, передбачення можливих коренів, умінь їх знаходження шляхом добору (якщо це можливо),  обирати найраціональніший. При цьому учні повинні згадати необхідний теоретичний матеріал, проаналізувати умову задачі, критично оцінити різні способи розв‘язання.

             Ірраціональні рівняння, як правило, викликають труднощі в розв’язанні. Головна причина – відсутність практичних навичок  проводити дослідження умови та можливих прийомів розв’язання.  Проте до більшості рівнянь можна застосувати навіть не один спосіб розв’язку.

Розглянемо  рівняння

Спробуємо розв’язати його різними способами.

І спосіб: введення однієї змінної.

ОДЗ:  -17

Нехай = ,  тоді 

Одержимо    

                                32-

тому

Перевіркою підтверджено, що число -1 є коренем заданого рівняння.

Відповідь: -1.

ІІ спосіб:  введення двох змінних.

Нехай = ,   =  

 Одержимо наступну систему рівнянь

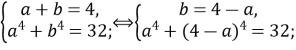
Коренем другого рівняння системи є число 2, тому

Відповідь:

ІІІ спосіб: застосування похідної функції.

Нехай  .

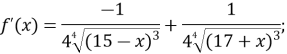
Знайдемо точки екстремуму функції розв’язавши рівняння

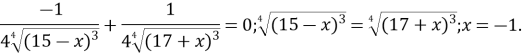
Точка розбиває область допустимих значень рівняння на два проміжки (-17; -1] та  [-1; 15).Досліджуємо на монотонність функцію на кожному з проміжків.

Тому функція на проміжку (-17; -1] є зростаючою, а на проміжку

  [-1; 15) – спадаючою. Граничне число кожного з проміжків число -1 є єдиним коренем заданого рівняння.

Відповідь: -1.

ІV спосіб: застосування нерівності між середнім арифметичним і середнім квадратичним.

Розв’язання.

         Двічі скористаємося нерівністю між середнім арифметичним та середнім квадратичним для

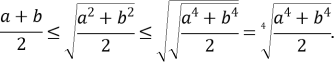
Одержимо

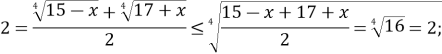
            Нерівність перетворилася в рівність. Це можливо за умови рівності доданків, тобто

Відповідь:  -1.

          Для розв’язання заданого рівняння способом застосування похідної теоретична скарбничка школярів має бути поповнена наступним теоретичним багажем.

В даному випадку спрацьовує така схема розв'язування:

● підбираємо один чи кілька коренів рівняння;

● доводимо, що інших коренів немає, при цьому використовуючи теореми про корені рівнянь або оцінку значень лівої та правої частини рівнянь.      

                                Теореми про корені рівняння

Теорема 1

у

           Якщо в рівнянні f(x) = а функція  f(x)

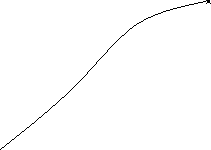                                                                 зростає (спадає) на даному проміжку

     у = а             у = f(x)                             то це рівняння може мати не більше

                                                                 ніж один корінь на цьому проміжку.

                 Функція неперервна.

 х

Теорема 2

             y=q(x) y=f(x)                 Якщо в рівнянні f(x) = q(x) функція f(x)       

                                                                 зростає  на деякому проміжку, а  q(x) -              

              а                                                 спадає на цьому самому проміжку (або 

                                                                 навпаки), то це рівняння може мати не      

                                                                 більше ніж один корінь на цьому     

                                                      х         проміжку. Обидві функції неперервні.      

         Справді , якщо функція монотонна, то таке рівняння має лише один корінь, бо для монотонної функції нерівним значенням аргументу відповідають нерівні значення функції. Графічно це означає, що пряма лінія, паралельна осі абсцис (графік функції – константи), не може перетинати графік монотонної функції більше, ніж в одній точці.

           Якщо – кусково-монотонна функція, то рівняння може мати не тільки більш як один корінь, але навіть нескінченне їх число, коли має нескінченне число проміжків монотонності. Проте їх не може бути більше, ніж число проміжків монотонності кусково-монотонної функції.

           Для дослідження монотонності функцій застосовуємо похідну.

 Отже, проведення уроків - «свято одного рівняння» сприяє формуванню предметних компетентностей, узагальненню та систематизації знань здобувачів освіти не лише з одної виучуваної теми, а й закріплення практичних навичок з основних прийомів розв’язання рівнянь та базових математичних закономірностей між математичними величинами, стане неоціненним багажем при складанні зовнішнього незалежного оцінювання та сформує міцні підвалини креативного мислення для майбутнього.