Стаття "Теоретичні основи та практичні прийоми розв’язання ірраціональних рівнянь традиційними способами"

Теоретичні основи  та практичні прийоми розв’язання

 ірраціональних рівнянь традиційними способами

         Тему «Ірраціональні рівняння» не можна віднести до легко засвоюваної. Її традиційне вивчення зосереджене в рамках курсу VIII – ХI класів, що дозволяє повноцінно враховувати вікові можливості здобувачів освіти у формуванні ряду предметних компетентностей, але часу на вивчення теми відведено небагато. Перш за все, відмітимо, що при викладі даної теми реалізуються багато загальних методичних особливостей, характерних для курсу в цілому. Але про це доцільно говорити лише у рамках програми старшої школи.

           Розглянемо ірраціональні рівняння, в яких змінна знаходиться тільки під знаком радикала.

  = 5;      = 3;     = 2;     = 1;     = 0;

  = 2;     = - 4;     = - 5.

         Основні методи для розв’язання таких рівнянь – піднесення правої і лівої частини до степеня і  використання властивості області значення кореня парної степені.

         Узагальнення поняття степеня дає змогу ввести ірраціональні рівняння загальнішого вигляду, а саме: коли змінна стоїть під знаком кореня довільного степеня або під знаком степеня з дробовим показником.

Ми розглядатимемо розв’язування ірраціональних рівнянь на множині дійсних чисел, тобто розв’язками рівнянь  можуть бути лише дійсні числа. Зазначимо, що при цьому під значеннями коренів парного степеня розуміють їх арифметичні значення, тобто вираз під коренем і сам корінь невід’ємні, а під значеннями коренів  непарного степеня – їх дійсні значення.

             Розв’язування ірраціонального рівняння полягає в зведені його до раціонального рівняння, що рівносильне заданому або є його наслідком.

Слід пам’ятати, що при переході до наслідку можливими є розширення області визначення рівняння і поява сторонніх коренів для заданого рівняння, тому в таких випадках перевірка коренів обов’язкова. Поява сторонніх коренів може статися в разі піднесення обох частин рівняння до однакового степеня.

          Під час розв’язування ірраціональних рівнянь користуються такими твердженнями:

1) f(x) = = = ,     k ;

2) f(x) = = = ,   k

3)

4) = f(x) =,    k

5) k

 

Розв’язуючи ірраціональні рівняння, треба мати на увазі наступне:

1. = q(x) ==>

                                                                                      

2. · q(x) = 0 ==>

або

3.    , або

4. = 0    (1)

,     або    

 Зауважимо, що треба дотримуватись рівносильності при розв’язуванні рівняння (1)

       

 

 

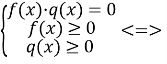
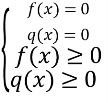
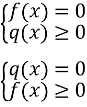
         Розглянемо на прикладах основні методи, які найчастіше застосовуються при розв’язанні досить непростих  ірраціональних рівнянь.

1. Піднесення в степінь

• Піднесення до квадрату правої та лівої частин рівняння

Приклад 1. Розв’язати рівняння

Розв’язання

          Можливе відокремлення будь-якого радикала або групи радикалів. В більшості випадків принципового значення це не має. Але іноді відокремлення одного радикала приводить до більш простого розв’язання.

В заданому рівнянні сума коефіцієнтів при змінній в першому та третьому підкореневих виразах дорівнює коефіцієнту при в другому підкореневому виразі. Тому доречно відокремити  другий радикал    Після піднесення до квадрата правої та лівої частин рівняння одержимо змінну лише під знаком радикала

                             =

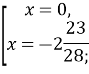
Перевіркою встановлюємо, що число є коренем заданого рівняння.

Відповідь: 

• Застосування формул суми та різниці кубів

 

Приклад 2.  Розв’язати рівняння

Розв’язання

)=

Оскільки

маємо                             3

 

Відповідь:   -6;  - 5,5;  -5.

 2. Виділення в підкореневому виразі повного квадрату

             Використаємо спосіб звільнення від   радикалу із застосуванням відомої тотожності =

 Приклад 1.   Розв’язати рівняння

 

Розв’язання.

Здійснюємо тотожні перетворення підкореневих виразів, одержимо

a)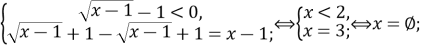

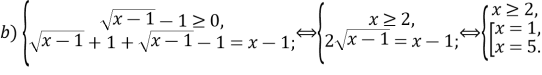
Перевіркою встановлено, що число є коренем заданого рівняння.

Відповідь: 

3. Введення нової змінної

            Введення нової змінної  особливо доречно застосовувати для ірраціональних рівнянь, які містять радикали з різними показниками, або підкореневі вирази радикалів – одинакові чи взаємно обернені вирази.

Приклад 1. Розв’язати рівняння

                                            .

Розв’язання.

ОДЗ:  всі дійсні числа, крім нуля.

           Здійснимо окремі тотожні перетворення обох частин рівняння. Помножимо обидві частини рівняння на

=

Заміна: маємо

 

 

 

14

   або ,  що не задовольняє умову

Відповідь:

Приклад 2. Розв’язати рівняння

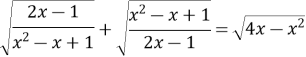
Розв’язання.

Заміна:  =t,  тоді ліва частина рівняння буде    

За відомою нерівністю Коші

Оцінюємо праву частину заданого рівняння

=

Рівність можлива за умови

 

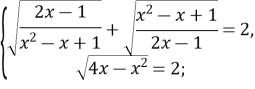
Розв’яжемо простіше рівняння

Одержане число задовольняє і друге рівняння системи.

Відповідь:  2.

Приклад 3. Розв’язати рівняння

Розв’язання.

ОДЗ: 

Заміна:  одержимо

+6t-7=0 

Перевіркою встановлюємо, що число є коренем заданого рівняння.

Відповідь: 

4. Застосування умови рівності добутку нулеві.

Приклад 1. Розв’язати рівняння

Розв’язання.

=

вираз  -  існує, тому   корінь заданого    

рівняння.

      

 

   

Відповідь: 

         Отже, уміння розв’язувати ірраціональні рівняння починається із абсолютного володіння традиційними прийомами  їх розв’язання. Враховуючи сучасні вимоги, що пред'являються до математичної підготовки здобувачів освіти на державній підсумковій атестації і на ЗНО для вступу у вищі навчальні заклади і той факт, що математика з 2021 року стане обов’язковим предметом на ДПА і дана тема є достатньо важкою для самостійного вивчення учнів, має сенс досить уважно здійснювати підбір завдань, що є різноманітними і вимагають акамуляції знань з різних розділів програми.