Стаття "Застосування акмеологічного підходу при вивченні геометрії"

Надточій Олександра Миколаївна,

вчитель математики Будищенської ЗОШ І-ІІІ ступенів ЧРДА

Застосування акмеологічного підходу при вивченні геометрії

Використовуючи стратегії творчого пошуку «Альпініст»,  «Квадратики»,

 «Поезія»,  «Збір грибів»,  «Спрощення»,  «Воскресіння» формую у школярів стратегіальне мислення в цілому, вчу висловлювати власну думку, розвивю логічні компетентності,  домогаюся усвідомленого розуміння. Оскільки рушієм розвитку є протиріччя між «можу» і «хочу» та «знаю» і «треба», то намагаюся учнів націлити на встановлення аналогій між даними задачі та базою знань конкретного учня в класі (групі, в які учні за бажанням об’єднуються). Варто зазначити: років 10 тому діти , за бажанням  об’єднувались за принципом « з достатнім та початковим рівнем знань», а нині «з достатнім та високим рівнем знань» та «початковим та середнім рівнем знань». Тому завдання добирати для кожної групи варто виважено, зазначивши зрозумілі лише вчителю, умовні позначки. Група «з достатнім та високим рівнем знань» самостійно, застосовуючи стратегією альпініста,  квадратики, поезію,  збір грибів,  спрощення,   розв’язує завдання самостійно або з незначною корекцією роботи вчителем, презентує результат роботи, відмічає усні кроки та етапи, які вимагали логічних міркувань.

Група  з  «початковим та середнім рівнем знань» потребує використання навідних запитань, застосування схем, більшої кількості прикладних задач не тільки розв’язувати, а й складати самим, виконувати рисунки, аплікації, поробки для створення психологічного настрою на роботу: дітям важливо, що вчитель поруч, вірить в них, радіє кожній їхній маленькій перемозі, підтримає, непомітно для інших, кожну особистість.  (Після контакту «очі в очі» діти з особливим натхненням продовжують працювати.

Прошу вибачення за такий ліричний крок в бік психології, та, нажаль, багато дітей у 5 -6 класі недоотримують родинного тепла, дружньої уваги, батьківської поваги, материнської любові. Вже семикласники, в силу своїх психофізичних особливостей, потребують такого контакту менше, вони впевненіші в собі. В класі є, так звана «дистанційна» парта (перша), за яку кожного разу сідають різні учні. Підтримка дитини поглядом допомагає стрімко йти до вершини розв’язання задачі.)

Тема 2. «Взаємне розташування прямих на площині.»

  Урок № 7. Тема .Розв’язування прикладних задач. Самостійна робота.    (СЛАЙД 1)                                                                                   

Серед рівних розумом – за однакових умов – переважає        той, хто знає геометрію .

                                                                                    Б. Паскаль     (СЛАЙД 2)   

• Основна мета: формувати ставлення учнів до математики як невід’ємної складової загальної культури людини, необхідної умови її повноцінного життя в сучасному суспільстві; забезпечити оволодіння учнями математичною мовою, формувати  здатність пояснювати та доводити математичні твердження.
•  Освітня: відтворити в пам’яті учнів означення та властивості вертикальних  та суміжних  кутів, дослідити значення градусної міри кута між прямими, сформувати математичні компетенції : процедурну (уміння розв’язувати типові задачі), логічну (володіння індуктивним та дедуктивним методами), технологічну(володіння сучасними математичними пакетами), дослідницьку (володіння методами дослідження практичних та прикладних задач), методологічну (уміння оцінювати доцільність використання математичних методів для розв’язування практичних та прикладних задач).
• Розвиваюча: узагальнити та систематизувати знання, уміння та навички, набуті учнями при вивченні тем: «Перпендикуляр. Відстань від точки до прямої. Кут між двома прямими, що перетинаються.» , розвивати варіативність та критичність мислення, здатність до аналізу та синтезу, вчити учнів складати прикладні задачі за готовими рисунками, формувати практичну та логічну компетенції шляхом розвитку  уміння  виконувати охайні побудови; відтворити в пам’яті учнів означення суміжних та вертикальних кутів, вчити обґрунтовувати та аргументувати гіпотези, застосовуючи раніше вивчені аксіоми, теореми, базові задачі та особистий досвід, розвивати  уміння працювати з підручником, шукати і використовувати додаткову навчальну інформацію, виокремлювати головне, формувати  здатності обґрунтовувати твердження, забезпечувати  оволодіння учнями мовою геометрії, розвивати  їх просторові  уявлення, розвивати уміння виконувати геометричні побудови за допомогою геометричних інструментів, привчати учнів застосовувати здобуті знання у навчальних і життєвих ситуаціях.
• Виховна: формувати  соціальні, комунікаційні  компетенції, застосовувати математичні методи у процесі розв’язування навчальних і практичних задач, розвивати уміння застосовувати здобуті знання у навчальних і життєвих ситуаціях; виховувати патріотизм, любов до праці, цікавість до вивчення геометрії, виховувати почуття власної гідності, привчати до виконання охайних рисунків.

Наочність і обладнання: набір демонстраційного креслярського приладдя, презентація до уроку, креслярське приладдя в кожного учня.

 Очікувані результати:

Учень/учениця:

• наводить приклади перпендикулярних прямих, знаходить, показує та будує перпендикуляр з даної точки до даної прямої
• пояснює: що таке  перпендикуляр та не перпендикуляр
• формулює: означення: перпендикулярних прямих, перпендикуляра
• вимірює та обчислює відстань від точки до прямої
• зображує та знаходить на малюнках перпендикуляр; не перпендикуляр 
• застосовує вивчені означення і властивості до розв’язування задач
• наводить приклади перпендикулярних прямих, перпендикуляра, опущеного зданої точки до даної прямої;

 Урок узагальнення та систематизації знань.

                    Хід уроку

1. Перевірка домашнього завдання.

 Самостійна робота контролюючого характеру.  (Воскресіння)

№ 7.1. Знайдіть градусні міри всіх кутів, які утворились при перетині двох прямих, якщо: а) всі кути рівні між собою (І в.); б)різниця двох з них 40˚ (ІІ в.); в) сума двох з них 140˚ (ІІІ в.); г) два кути відносяться як 3:6 (І в.);  д) сума  двох з них 60˚ (ІІ в.); е) три з них рівні між собою (ІІІ в.); є) сума трьох кутів дорівнює 280˚ градусів (І в.); ж) один з утворених кутів у  два рази менший за другий (ІІ в.); з) один з утворених кутів у  три рази більший за другий (ІІІ в.).

№ 7.2. Накресліть пряму, побудуйте точку, що не належить їй, знайдіть відстань від точки до прямої. Відповідь обґрунтуйте.

2. Мотивація навчальної діяльності учнів.

(Спрощення)

У будівництві, архітектурі, ландшафтному дизайні, проектуванні застосовуються геометричні знання. Людям, які прагнуть бути успішними, слід добре знати геометрію та вміти застосовувати вміння на практиці.     (СЛАЙД 3)

3. Повідомлення теми, мети та завдань уроку.

(Альпініст)

4. Узагальнення окремих фактів, подій і явищ.

(Спрощення)

Учні об’єднуються в групи. (Прийом кластер. Кластер – це спосіб гафічної організації матеріалу, що дозволяє зробити наочними ті розумові процеси, які відбуваються при зануренні в ту чи іншу тему. Іноді такий спосіб називають «наочним мозковим штурмом».

 Послідовність дій проста і логічна:

1. Посередині чистого аркуша написати ключове слово, яке є «серцем» ідеї, теми.

2. Навколо «накидати» слова або пропозиції, що виражають ідеї, факти, образи відповідні для даної теми. (Модель «планета її супутники»)

3. Слова, що з’явилися, з’єднуються  прямими лініями з ключовим поняттям. У кожного з «супутників» у свою чергу теж з’являються «супутники», встановлюються нові логічні зв’язки.

У підсумку виходить структура, яка графічно відображає наші роздуми, визначає інформаційне поле даної теми.

У роботі над кластерами необхідно дотримуватись таких правил

Не боятися записувати все, що приходить у голову. Дати волю уяві та інтуїції. Продовжувати роботу, поки не скінчиться час або ідеї не вичерпаються. Постаратися побудувати якомога більше зв’язків. Не слідувати за заздалегідь визначеним планом.)

(Альпініст)

Повторюємо: а) означення перпендикуляра, основи перпендикуляра, перпендикулярних прямих; б) як знайти кут між двома прямими, що перетинаються; в) як знайти відстань від точки до прямої; г) які задачі називаємо прикладними?

5. Повторення і узагальнення понять та засвоєння відповідної системи знань.

(Поезія)

Учні виконують Гімн України:

«Ще не вмерла України ні слава ,ні воля

Ще нам , браття молодії , усміхнеться доля.

Згинуть  наші воріженьки як роса на сонці

Запануєм і ми, браття, у своїй сторонці…».

(Воскресіння)

 Обчислюють кількість приголосних у четвертому рядку  ті учні , хто працює на І варіанті. На дошці записані слова: «Справедливі  семикласники».  Кількість приголосних підраховують  ті учні , хто працює на ІІ варіанті.  Знаходять різницю. В результаті отримуємо 2.

(Квадратики)

№ 7.3. Побудуйте дві точки. Проведіть пряму l. Зобразіть точку M, яка не належить даній прямій.

№ 7.4. Проведіть пряму MN, що перпендикулярна до прямої l.

Завдання для команди «Сміливі»

№7.5. Знайдіть відстань від точки М до прямої l.

№ 7.6. Зробіть висновок.

Завдання для команди «Спритні»

№ 7.5. Знайдіть довжину МК.

№ 7.6. Порівняйте МК і MN.

№ 7.7. Зробіть висновок.

Завдання для команди «Сильні»

№ 7.5. Позначте точку О – точку перетину прямих МК і MN.

№ 7.6. Знайдіть величину кута між прямими МК і MN.

№ 7.7. Зробіть висновок.

6. Повторення і систематизація основних теоретичних положень  і провідних ідей при розв’язуванні прикладних задач

(Воскресіння)

№ 7.8. Висота «гірки» на дитячому майданчику  2 метри. Побудуйте ескіз «гірки» для дітей молодшого та старшого дошкільного віку (автономні спуски) у масштабі 1:100. (СЛАЙД 4, 5)

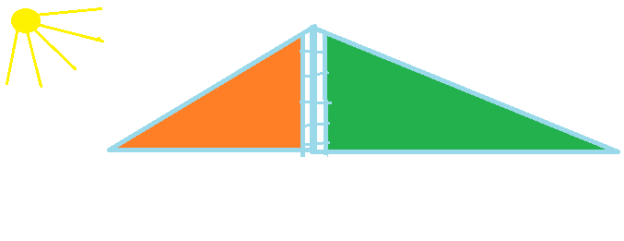
(Збір грибів)

№ 7.9. Глибина басейну 3 метри. Накресліть ескіз східців до басейну. (СЛАЙД 6)

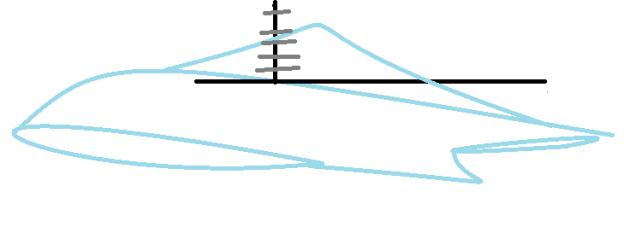
(Збір грибів)

№ 7.10. Відстані від школи до будинків Тараса, Максима та Богдана відповідно дорівнюють 600м, 700м та 200м. Побудуйте план. (СЛАЙД 7)

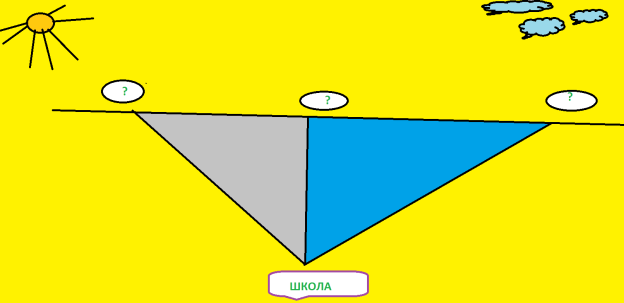
(Спрощення)

№ 7.11. Довжини паперових гірлянд, які виготовили Іванна, Дарина та Софія, відповідно дорівнюють 2м, 3м,і 4м. Гірлянди прикріпили до верхівки ялинки.  Накресліть схему . (СЛАЙД 8)

 Домашнє завдання.

(Збір грибів)

У результаті перетину двох прямих утворились 4 кути, кожен з яких менший від розгорнутого. Знайдіть градусну міру кожного кута, якщо:

          а) сума двох кутів дорівнює 78°;

          б) різниця двох кутів дорівнює 42°;

          в) один з кутів у 5 разів менший від іншого;

          г) один з кутів у 2 рази менший від суми двох інших;

          д) сума трьох кутів дорівнює 300°;

          е) сума трьох кутів більша від четвертого на 100°.

8. Підсумок уроку.

(Воскресіння)

Інтерактивна гра. Продовжте речення:

1. Особисто для мене незвичним на уроці було…
2. Зацікавило мене…
3. Сподобалось …
4. Я навчився (навчилася)…
5. Тепер я вмію…
6. Запам’яталось…

Пояснювальна записка

МОН України Математика. До «Програми для загальноосвітніх навчальних закладів. 5-12 класи»

У розробці вміщено задачі за готовими рисунками, прикладні, творчого та дослідницького характеру, які, на мою думку, сприяють розвитку пізнавальної активності та самостійної діяльності учнів.

Даний електронний матеріал або його елементи варто використовувати у навчально - виховному процесі при вивченні геометрії у7 класі загальноосвітньої школи.

Список використаних джерел:            

                                         Література:

1. Електронний посібник «Клуб веселих математиків», укладач Педан Н.І.

2. Електронне  «Портфоліо  Ходорковська»

3. 08841d_53dad8da_XL.jpq

 4. .jpq

5. node-5711-osb-dom. .jpq

6. Стаття О. Р. Юрка «Акмеологічні стратегії розвитку логічного мислення, або як навчити учнів мислити».