"Суд над Піфагором". Урок геометрії

Зеленодольська загальноосвітня школа І-ІІІ ст № 2

 

 

 

Декада педагогічної майстерності

 

 

 

 

 

 

Урок геометрії в 8-А класі

«Суд над Піфагором»

 

 

 

 

Підготувала: Толокнєєва Любов Петрівна,

вчитель математики вишої категорії

 

 

 

 

 

 

 

 

2018 р.

Мета уроку:

• узагальнити і систематизувати знання учнів по темі «Теорема Піфагора», довести значимість теореми, її практичне застосування;
• показати міжпредметний зв’язок з алгеброю, історією, астрономією;
• розвивати в учнів вміння логічно пояснювати і відстоювати свою думку.

Тип уроку: урок узагальнення, систематизації і застосування знань.

Оснащення: 1) наочність: ілюстрації, фото, карта;

                        2) картки із завданнями для самостійної роботи;

                        3) таблиця, на якій показано застосування теореми Піфагора для   

                        знаходження арифметичного квадратного кореня;

                        4) Костюми: Туніка – для Піфагора;

                        Судейські шапки – для судді і прокурора.

Форма проведення: урок-суд.

 

Перебіг уроку

І. Вступ. Мотивація навчальної діяльності. 

Вчитель.

Як сказав давньогрецький вчений, філософ і логік – Аристотель:

«Розум полягає не лише в знаннях,

 але й у вмінні застосовувати ці знання».

І тому я пропоную тему нашого уроку: розв’язування задач на застосування теореми Піфагора.

На попередніх уроках ми вивчили «найвеличнішу теорему» - теорему Піфагора. В будь-якій задачі, де ми стикаємося з прямокутним трикутником завжди є місце для теореми Піфагора. А прямокутний трикутник зустрічається і в квадраті, і в прямокутнику, ромбі, трапеції, в колі і в багатьох інших фігурах.

Тому метою нашого уроку буде: узагальнення і систематизація знань про властивості прямокутного трикутника; застосовування набутих знань, умінь і навичок до розв’язування задач які містять прямокутний трикутник, безпосередньо застосовування теореми Піфагора для знаходження відстаней між точками.

Отже, бажаю всім успіху! Запрошую всіх вас на наш урок «Суд над Піфагором».

 

ІІ. Основна частина.

Суддя: Добрий день, сідайте. Слухається справа вченого Піфагора і славнозвісної          

              його теореми. Прокурор, зачитайте звинувачувальний вердикт.

Прокурор: звинувачується вчений Піфагор за те, що він назвав своїм ім’ям теорему, яка була відома ще стародавнім вавилонським вченим та іншим народам стародавнього Сходу ще за 2000 р. до н.е. Звинувачується теорема Піфагора за те, що вона своїм існуванням не давала спокійно жити і іншим вченим, які не досипаючи не одну ніченьку прийшли до своїх доведень даної теореми, відмінних від Піфагорового. І тепер зафіксовано в науковій літературі 367 доведень цієї теореми.

Суддя: Шановний Піфагор, я бачу, ви не наймали собі адвоката, і ми розуміємо, що свій захист ви побудуєте самі. Отже, шановні присяжні і всі присутні, слухаємо Піфагора.

Піфагор: Я, Піфагор – син Мнесарха із Самосу, на свій захист висуну слідуюче: Живучи у стародавній Греції і прийшовши до теореми, класичне формулювання якої «Якщо сторони прямокутного трикутника є сторонами квадратів, то площа квадрата побудованого на гіпотенузі, дорівнює сумі площ квадратів, побудованих на катетах», стверджую, що до неї прийшов сам, не знаючи про існування даного твердження і його доведення у стародавніх єгиптян і вавілонян.

Довівши теорему, я доніс її до своїх учнів, які навчаються в моїй школі. Один з них навіть доведення може продемонструвати.

Учень 1: формулює ще раз теорему і надає доведення (на дошці).

Учень 2: Але дуже легко знайти безліч чисел, знаючи не лише трійку чисел a, b, c і помножуючи ці числа на будь-яке натуральне число n. Справді, якщо , то

Прокурор: збереглася давня легенда, що на честь свого відкриття Піфагор приніс у жертву бика, а з інших свідчень – навіть сто биків.

Учень 3: Але Діоген Лаертський у книзі «Про життя, вчення і висловлювання знаменитих філософів» писав: «Жертви Богам Піфагор приносив необтяжливо, догоджаючи їм борошном, коржами, ладаном, миррою і дуже рідко – тваринами, крім хіба що молочних поросят. І навіть коли він довів свою теорему, то приніс у жертву бика, виготовленого з пшеничного тіста».

Учень 4: Про цілочислові прямокутні трикутники знали ще в стародавньому Вавілоні (ІІІ тисячоліття до н.е.) і застосували їх для вимірювальних робіт.

За допомогою теореми Піфагора можна геометрично знаходити значення квадратних коренів з цілих чисел. Потрібно виконати побудови для цього, як добре показано на малюнку.

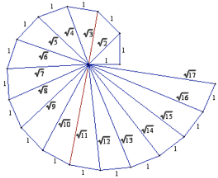
Суддя: Добре, це ми бачили деяких учнів вашої школи. А зараз, я б хотіла перевірити знання усіх учнів.

Робота в групах (завдання на аркушах А4, див. додаток А)

/після розв’язання відповіді вивішуються на дошку, доповнюються усними коментарями учнів, по 2 учня з кожної групи/

 

Суддя: Добре, продовжується слухання справи вченого Піфагора. Хто має інформацію по суті?

Учень 4: Я хочу виступити в захист вченого і його теореми. Важливість даної теореми ілюструє слідуючий факт. Наприкінці XIX ст. було відкрито на марсі «канали», які вважали штучними. Для налагодження зв’язку з марсіанами запропонували на величезному просторі Західно-Сибірської площини побудувати гігантську геометричну фігуру, яка б світилась, - рисунок теореми Піфагора, бо вважали, що ця теорема справедлива скрізь і що жителі будь-якої планети повинні зрозуміти такий сигнал. Передбачили, що, побачивши це зображення, марсіани зроблять висновок і дадуть відповідь також мовою математики.

Адже математику вважають універсальною мовою Всесвіту!

Учень 5: Я також хочу виступити у захист теореми і вченого Піфагора. Прямокутні трикутники, сторони яких виражаються натуральними числами, називають піфагоровими трикутниками. Піфагорових трикутників безліч. Це наприклад прямокутні трикутники зі сторонами 5, 12 і 13; 6, 8 і 17 і т.д.

Піфагор: Якщо суддя і шановні присяжні дозволять, то я далі продовжу свій захист. Дану теорему люди взяли на озброєння при отриманні прямих кутів у тесаних плит, для побудови пірамід Хефрена (у Єгипті), користуючись шнурком, який ділили на частини в 5, 4 і 3 одиниці довжини. Тому і трикутник зі сторонами 3, 4 і 5 почали називати єгипетським. І справді, якщо

                                                  , то

                                                  ,

                                                  ,

                                                 

Учні, продемонструйте шнурок!

/ Демонструємо мотузку з вузликами у групах.

 

Піфагор: Стародавній спосіб побудови прямих кутів з використанням відношення сторін в єгипетському трикутнику іноді застосовується на будівництві і тепер.

Суддя: Шановний Піфагор, слухаючи ваш захист, я зрозуміла, що ваші учні є гідними свого вчителя і можуть показати свої знання при розв’язуванні задач, на застосування теореми Піфагора.

Отже, викликаються свідки – (з кожної команди по 1 учню).

Задача 1: знайдіть сторони ромба, якщо його діагоналі рівні 24 см і 18 см.

           ABCD – ромб, АС ┴BD, AC=78 см, BD=24 см

      AK=AC=(см)

      BK=BD=(cм)

                         АКВ – прямокутний трикутник, за т.Піфагора:

               

      (см)

      Відповідь: AB=BC=DC=AD=15 см.

      

Задача 2 : Металевий стержень довжиною 70 см треба зігнути під прямим кутом так, щоб відстань між його кінцями дорівнювала 50 см. Де має бути точка згину?

За теоремою Піфагора:

    

    

                | :2

    

    

    

    

    або

    

Задача 3.

У рівнобічну трапецію з основами 4 см і 16 см вписано коло. Знайдіть радіус кола.

Колективне обговорювання задачі:

1. У рівнобічної трапеції бічні сторони рівні.
2. Відрізок, який відтинає висота на нижній основі, дорівнює піврізниці основ.
3. Утворюються два прямокутних трикутника.
4. Можна застосувати теорему Піфагора.
5. Якщо в трапецію можна вписати коло, то сума основ дорівнює сумі бічних сторін.
6. Радіус вписаного кола дорівнює половині висоти трапеції.

   В   4   С                                   Дано: ABCD – рівнобічна трапеція

                                                                           описана навколо кола,

                                                                           BC AD, AB = CD,

                                                                            BC = 4 см, AD = 16 см.

                                                                            Знайти: r.

Розв’язання.

Так як в трапецію можна вписати коло, то сума основ дорівнює сумі бічних сторін:

АВ + СD = ВС + АD; АВ = СD; 2 АВ = 4 + 16 = 20 (см); АВ = 10 см.

. Проведемо висоту ВК, – прямокутний;

АК = (см).

За теоремою Піфагора:  ; тоді ;

ВК = (см); r = 8 : 2 = 4 (см).

Відповідь: 4 см.

 

Суддя: Шановний Піфагоре. Останнє, що би хотіла побачити, це те, як учні зможуть здати залік.

Математична вікторина

1. Ім’ям якого відомого математика складається з трьох складів: перший склад  - число, другий – нота, а третій – одне з імен давноєгипетського бога Сонця?                                             (Пі – фа – гор)
2. У якому столітті жив Піфагор?              (  VІ ст.. до н. е. )
3. Скільки століть минуло з часу життя Піфагора?  (27 століть)
4. З якого виду спорту Піфагор був олімпійським чемпіоном?   ( З кулачного бою на олімпіаді в 548 р. до н. е.)
5. Який нещасний випадок стався на цій олімпіаді?   ( Спостерігаючи за боєм Піфагора, на трибуні помер відомий математик Фалес)
6. Що ви знаєте про числа 5, 6, 7, 8, 9, 13, 17?      (Піфагорійці вважали, що 5 символізує колір, 6 – холод, 7 – розум, здоров’я та світло, 9 – постійність;  ненависними були числа 13 та 17) 
7. Які математичні твердження належать Піфагору?   (Суми послідовних непарних чисел, починаючи з одиниці, є точними квадратами. Всяке непарне число є різницею квадратів)
8. Що ви можете сказати про множину ірраціональних чисел?   (Цей вид чисел відкрив Піфагор, шукаючи діагональ квадрата зі стороною 1)
9. Які числа характеризують основні музичні інтервали? (1, 2,3,4. Тривалість нот «раз – і два – і три – і…».)
10. Як інакше називається трикутник зі сторонами 3,4,5? (єгипетський)
11. Що ви знаєте про Піфагорові числа? ( це трійки чисел, що задовольняють умову а² + в² = с², де а, в, с – взаємно прості)

 

Суддя: Заслухавши всі за і проти, що прозвучали, суд присяжних і я постановляю:

1. Для того, щоб ви пережили ще раз задоволення при розв’язуванні задач на застосування теореми Піфагора вам пропонується виконати слідуюче завдання:

«У центрі квадратного озерця, ширина якого 10 кроків, росте очерет, висота його над поверхнею 1 крок. Якщо стоячи на березі водойми потягнути очерет до середини будь-якої сторони, то він доторкнеться до краю озера. Яка глибина озера?»

2. Вчений Піфагор теорему самовільно не привласнював, а навпаки, вдячні нащадки за те, що він дав перше повноцінне доведення цієї теореми, нарекли її його іменем.
3. Теорема Піфагора є одним з найважливіших геометричних твердження і відіграє основну роль у геометричних обчисленнях.

          Судове засідання закінчено. До побачення!

 

Оцінювання.

Домашнє завдання:

Вивчити доведення теореми Піфагора (§ __).

Вирізати з паперу 3 квадрати зі сторонами, що дорівнюють сторонам накресленого на папері прямокутного трикутника, і за допомогою розрізування впевнитись, що площа найбільшого квадрата дорівнює сумі менших.

Розв’язати № ___________________________

Повторити § 7.

 

 

 

 

 

 

 

 

 

 

 

 

   

 

        

 

 

 

 

 

 

 

 

 

 

Так сказав Піфагор

•        Живи з людьми так, щоб твої друзі не стали недругами, а недруги стали друзями.
•        Твори велике, не обіцяючи великого.
•        Не заплющуй очей. Коли хочеш спати, не проаналізувавши всіх своїх учинків за минулий день.
•        Тимчасова невдача краще тимчасової удачі.
•        Не роби нічого ганебного ні в присутності інших, ні таємно. Першим твоїм законом має бути повага до самого себе.
•        Лише неблагородна людина здатна в очі хвалити, а поза очі злословити.
•        Роби лиш те, що в майбутньому не засмутить тебе.
•  Усе впорядковується відповідно до чисел.

Додаток А

Робота в групах

 

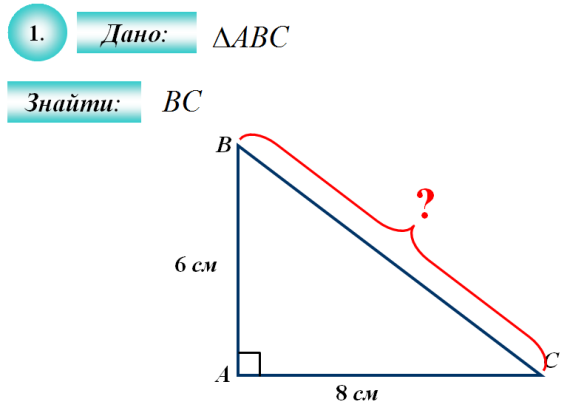
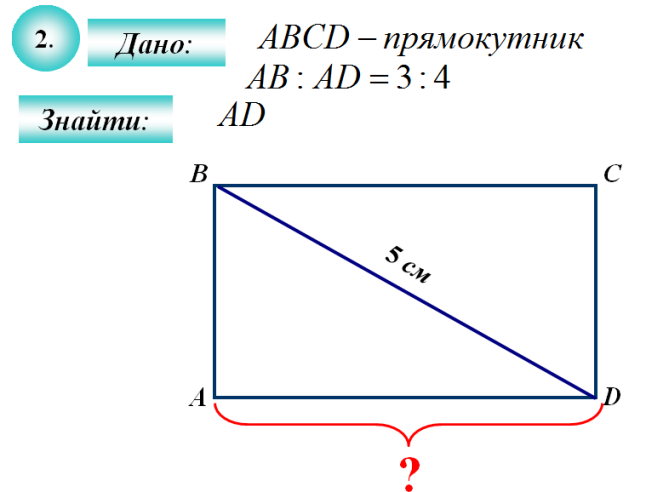
Додаток А

Робота в групах

 

 

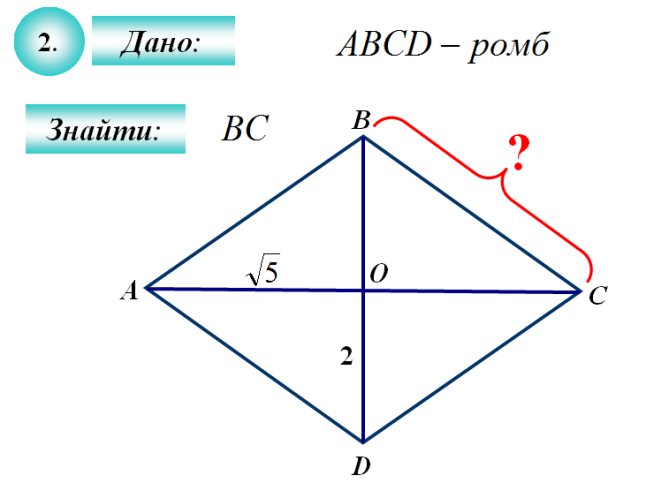
Додаток А

Робота в групах