Сума кутів опуклого многокутника
Важливим завданням вчителя є виявлення і розвиток здібностей і навчальних можливостей кожного учня. Цього можна досягти впровадженням різних форм навчання. Однією з таких форм є нетрадиційні уроки, які активізують діяльність учнів, зацікавлюють їх, розвивають здібності і нахили, самостійність у діях і мисленні, сприяють розвитку творчості, виявленню індивідуальних особливостей. Саме тому я пропоную один із таких уроків, який може бути використаний для роботи з учнями у 8 класі.
Відділ освіти Сихівської адміністрації
Методичне об’єднання вчителів математики СЗШ № 73

Підготувала вчитель математики,
спеціаліст вищої категорії,
старший вчитель
Кондрин Леся Петрівна
Навчальна мета уроку: ознайомити учнів з теоремою про суму кутів
опуклого многокутника; формувати вміння
застосовувати її в ході розв’язування задач.
Розвиваюча мета уроку: розвивати вміння працювати самостійно;
сприяти активізації розумової діяльності учнів;
розвивати бажання застосовувати набуті знання,
вміння та навички для досягнення поставленої мети;
Виховна мета уроку: виховувати інтерес до вивчення геометрії ;
активність, увагу, кмітливість.
Тип уроку: засвоєння нових знань.
Обладнання до уроку: комп’ютер, мультимедійний проектор, екран.
Хід уроку

- Організаційний момент.
- Вступ.
Давньогрецький філософ, учень Сократа та вчитель Аристотеля, Платон (427-347р. до н. е. ) був засновником філософської школи в Афінах – «Академія».
На вході до «Академії» викарбовано знаменитий вислів:
 «Нехай не входить сюди не навчений
«Нехай не входить сюди не навчений
геометрії!»
А зараз ми побачимо, чи змогли б ви зайти до «Академії», чи володієте ви знаннями із геометрії.
Перевірка знань проводиться у формі гри по турах.
I тур гри.
- Перевірка домашнього завдання
Проводиться шляхом обговорення з місця заданих задач.
- Ви правильно виконали домашнє завдання, отож можете зайти до Академії Платона.
- Але, щоб рухатись далі, ви повинні пройти II тур.
Учні пишуть математичний диктант, один з учнів працює на відкидній дошці. Після закінчення диктанту учні здійснюють взаємоперевірку.
II тур гри.

Математичний диктант:
1. За рис. 1 назвіть:
а) фігуру; б) сторони фігури; в) вершини фігури;
г) діагоналі фігури; д) кількість діагоналей фігури;
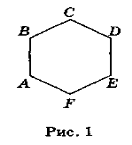 е) кількість кутів фігури; ж) загальну кількість
е) кількість кутів фігури; ж) загальну кількість
зовнішніх кутів фігури.
2. Закінчіть речення.
1) Замкнена проста ламана, у якій сусідні ланки не лежать на одній
прямій, називається … многокутник
2) Якщо кінці ламаної збігаються, то вона називається …замкнена
3) Відрізок, який сполучає несусідні вершини многокутника,
називається … діагональ
4) Якщо ламана не має самоперетинів, то вона називається …простою
5) Кут, суміжний із внутрішнім кутом многокутника при даній
вершині, називається …зовнішнім
6) n – кутник має … 0,5n(n-3) діагоналей.
А щоб потрапити у творчу лабораторію «Академії», ви повинні пройти III тур.
III тур гри.
 III. Актуалізація опорних знань учнів.
III. Актуалізація опорних знань учнів.
Запитання до класу:
1) Скільки діагоналей можна провести з однієї вершини n – кутника? n - 3
2) На скільки трикутників розіб’ють n – кутник діагоналі, проведені
з однієї його вершини? n - 2
3) Чому дорівнює сума кутів трикутника? 180
4) Чому дорівнює сума кутів чотирикутника? 360
 - «Природа розмовляє мовою математики: букви цієї мови – кола, многокутники та інші математичні фігури», - писав видатний італійський фізик, механік, астроном і математик Галілео Галілей .
- «Природа розмовляє мовою математики: букви цієї мови – кола, многокутники та інші математичні фігури», - писав видатний італійський фізик, механік, астроном і математик Галілео Галілей .
І саме многокутникам в геометрії відведено велику роль. Без перебільшення можна сказати, що вся геометрія базується на цьому понятті. Серед метричних властивостей многокутників однією з важливих є властивість суми кутів.
- І ось ми вже з вами у творчій лабораторії «Академії», де будемо займатись дослідницькою діяльністю і знайдемо, чому дорівнює сума кутів опуклого многокутника.
IV. Формулювання теми, мети і завдання уроку.
Діти не повинні вивчати ніяких правил,
а самі відкривати їх.
К. Д. Ушинський.
V. Вивчення нового матеріалу:
 1. Теорема про суму кутів опуклого n – кутника
1. Теорема про суму кутів опуклого n – кутника
Учні за рис. 2 та 3 і планом доводять, що сума кутів опуклого n – кутника дорівнює ![]()
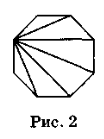
План доведення :
I – й спосіб
- Проведіть з однієї вершини n – кутника діагоналі.
- Запишіть кількість отриманих трикутників.
- Закінчіть фразу й заповніть пропуски:
Оскільки сума кутів одного трикутника …, а таких трикутників …, то сума кутів n – кутника, яку можна обчислити за формулою = … .
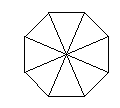
Рис. 3
II – й спосіб
- Виберіть довільну внутрішню точку опуклого n – кутника, та з’єднайте її з усіма вершинами многокутника.
- Запишіть кількість отриманих трикутників зі спільною вершиною у даній точці.
- Чому дорівнює сума всіх кутів при цій вершині?
- Чому дорівнює сума усіх кутів трикутника?
-
Продовжіть:тоді …
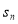
 +
+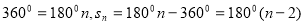
 2. Сума зовнішніх кутів опуклого n –кутника
2. Сума зовнішніх кутів опуклого n –кутника
Запитання до класу:
- Чому дорівнює сума внутрішнього й суміжного з ним зовнішнього кутів n – кутника?
- Чому дорівнює сума всіх внутрішніх і зовнішніх кутів n – кутника?
- Чому дорівнює сума всіх внутрішніх кутів n – кутника?
- Чому дорівнює сума зовнішніх кутів n – кутника?
Таким чином, формулюється опорний факт:
Сума зовнішніх кутів n – кутника, взятих по одному при кожній вершині, дорівнює ![]() .
.
VI. Первинне закріплення нового матеріалу.
 1. Знайдіть суму внутрішніх кутів: а) дванадцятикутника;
1. Знайдіть суму внутрішніх кутів: а) дванадцятикутника;
б) сімнадцятикутника.
2. Скільки сторін має многокутник, якщо сума його внутрішніх
кутів дорівнює ![]() ?
?
3. Чи може сума кутів многокутника дорівнювати ![]() ?
?
4. Скільки сторін має многокутник, якщо всі його кути рівні й
зовнішній кут при вершині становить ![]() ? ( Задача № 676 )
? ( Задача № 676 )
5. Знайдіть кількість сторін опуклого многокутника, у якому
сума внутрішніх кутів на ![]() більша від суми зовнішніх.
більша від суми зовнішніх.
6. Опуклий многокутник має 54 діагоналі. Знайдіть кількість
його сторін і суму кутів.
 VII. Підбиття підсумків уроку. Рефлексія.
VII. Підбиття підсумків уроку. Рефлексія.
Учням пропонується оцінити результати уроку, відповівши на такі запитання:
- Про що нове ви дізналися на уроці?
- Чи досягли поставленої мети?
-
 Що сподобалося вам на уроці?
Що сподобалося вам на уроці?
VIII. Домашнє завдання.
- Теоретичний матеріал параграфа 15 підручника.
-
Розв’язати задачі
 № 672, № 688, № 692.
№ 672, № 688, № 692.


- Г. П. Бевз, В. Г. Бевз, Н. Г. Владімірова, Геометрія: Підручник для 8 кл.
середніх загальноосвітніх закладів. К. : Вежа, 2008.
- В. С. Шевчук, Геометрія: Навчальний посібник для 9 кл. Тернопіль:
Навчальна книга – Богдан, 2004.
- Т. Л. Корнієнко, В. І. Фіготіна, Геометрія: Розробки уроків для 8 кл.
Х. : Видавництво – Ранок, 2009.

Платон (427-347р. до н.е.)– древньогрецький філософ, запропонував терміни «аналіз», «синтез». Обґрунтував метод доведення від супротивного, розробив методику розв’язування задач на побудову.
Тетраедр, октаедр, гексаедр (куб), додекаедр, ікосаедр називають ще платоновими тілами.
Іменем Платона названо кратер на видимій стороні Місяця.
Галіле́о Галіле́й (15 лютого 1564 — 8 січня 1642) — видатний італійський мислитель епохи Відродження, засновник класичної механіки, фізик, астроном, математик, один із засновників сучасного експериментально-теоретичного природознавства, поет і літературний критик.
Син музиканта Вінченцо Галілея.

1


про публікацію авторської розробки
Додати розробку
