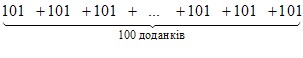Сума n перших членів арифметичної прогресії

Сума n перших членів арифметичної прогресії

Розглянемо скінченну арифметичну прогресію a₁, a₂, a₃, ..., a_n–2, a_n–1, a_n.

Суму членів цієї прогресії позначимо S_n.

Тобто,

S_n = a₁ + a₂ + a₃ + ... + a_n–2 + a_n–1 + a_n.                                  (*)

Виведемо формулу для знаходження цієї суми.

Спочатку розглянемо задачу, розв’язання якої підкаже, як знайти ідею для виведення шуканої формули.

Розглянемо арифметичну прогресію

1, 2, 3, ..., 98, 99, 100

і знайдемо суму її членів.

Запишемо шукану суму двома способами і додамо отримані рівності:

Маємо: 2S₁₀₀ = 101  100, S₁₀₀ = 5050.

Розповідають, що видатний німецький математик Карл Гаусс (1777 – 1855 рр.) додумався до такого розв’язання у віці 5 років.

Скористаємося описаним прийомом для знаходження суми (*).

Запишемо суму S_n двома способами. Спочатку запишемо суму, перший доданок якої дорівнює a₁, а кожний наступний доданок отримано з попереднього додаванням різниці d. Потім запишемо суму, перший доданок якої дорівнює a_n, а кожний наступний доданок отримано з попереднього відніманням різниці d. Маємо:

S_n = a₁ + (a₁ + d) + (a₁ + 2d) + ... + (a₁ + (n – 2)d) + (a₁ + (n – 1)d),

S_n = a_n + (a_n – d) + (a_n – 2d) + ... + (a_n – (n – 2)d) + (a_n – (n – 1)d).

Додавши ці рівності, отримаємо:

.

Вираз, який стоїть у правій частині останньої рівності, є сумою n доданків, кожний з яких дорівнює a₁ + a_n.

Тоді 2S_n = (a₁ + a_n)n,

.

Отримана рівність є формулою суми n перших членів арифметичної прогресії.

Підставивши до цієї формули замість a_n вираз a₁ + d(n – 1), отримаємо:

,

.

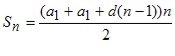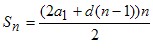Останньою формулою зручно користуватися тоді, коли задано перший член і різницю прогресії.

Приклад 1.

Знайдіть суму всіх трицифрових чисел, які кратні 6.

Розв’язання.

Дані числа утворюють арифметичну прогресію, перший член якої a₁ = 102, а різниця d = 6. Тоді a_n = 102 + 6(n – 1) = 6n + 96. Знайдемо кількість членів цієї прогресії. Оскільки a_n < 1000, то маємо:

6n + 96 < 1000;

6n < 904;

n < 150.

Отже, n = 150. Тоді шукана сума  = 82 350.

Відповідь: 82 350.

Приклад 2.

Сума сімдесяти п’яти перших членів арифметичної прогресії дорівнює 450. Знайдіть тридцять восьмий член прогресії.

Розв’язання. Нехай перший член прогресії та її різниця дорівнюють a₁ і d відповідно. Тоді сума сімдесяти п’яти перших членів S₇₅ = 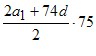 = 75(a₁ + 37d) = 450. Звідси маємо: a₃₈ = a₁ + 37d = 450 : 75 = 6.

Відповідь: 6.