Урок. Застосування інтеграла для обчислення площ плоских фігур.

Тема:

Застосування інтеграла до обчислення площ плоских фігур.

Мета уроку:

 удосконалити навички учнів обчислювати визначений інтеграл і знаходити площі криволінійних трапецій;

провести діагностику знань і вмінь учнів з даної теми;

розвивати обчислювальні навички, уміння лаконічно й чітко формулювати думку;

виховувати самостійність, толерантність, уміння працювати в групі.

Цілі:

формувати вміння записувати формули для знаходження площ плоских фігур;

застосовувати отриманні знання для обчислення площі прямолінійної трапеції, розвивати уміння працювати в групах  .

Формувати:

 спілкування державною мовою ( уміння грамотно формулювати означення, висловлювати власну думку рідною мовою );

математичну компетентність ( оперувати числовою інформацією, розв’язувати задачі математичного змісту, інтерпретувати та оцінювати результати);

інформаційно – цифрову компетентність ( уміння структурувати дані, складати алгоритм до розв’язування задачі ).

Тип уроку: удосконалення знань, умінь і навичок.

 

                                                Хід уроку

1. Організаційний етап.
2. Перевірка домашнього завдання.

 

На мультимедійній дошці подано розв’язки завдань, учні взаємоперевіркою виправляють помилки.

 

3.                 Актуалізація опорних знань.

 

Спілкування «Питання-відповідь».                                             

 

1. Сформулюйте означення визначеного інтеграла.
2. У чому полягає геометричний зміст визначеного інтегралу.
3. Запишіть на дошці властивості визначеного інтегралу.
4. Сформулюйте означення криволінійної трапеції.
5. На яких рисунках зображено криволінійну трапецію?

 

 

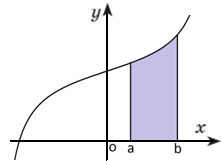
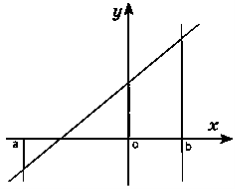
А                                                    Б                             

  

 

 

 

 

 

 

 

 

 

 

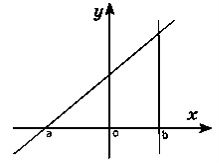
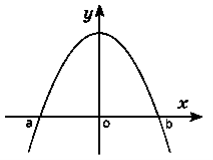
     В     Г

 

 

 

 

 

6. Запишіть на дошці формулу Ньютона-Лейбніца.
7. Як за допомогою визначеного інтеграла обчислити площу криволінійної трапеції.
8. Знайдіть площу заштрихованої фігури на рисунках

 

1.                                                    2)

 

 

 

 

 

 

 

9. Площа якої фігури виражається інтегралами:

 

 

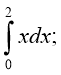
а)                б)                     Виконайте схематичний рисунок.

 

 

  10. Запишіть за допомогою інтеграла площі фігур, зображених на

       рисунку.

 

 

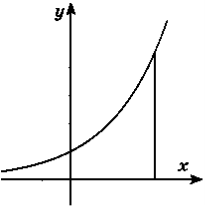
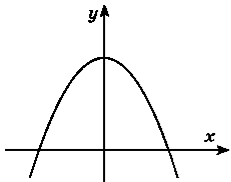
        а) 2   y₌2-x²                            б)                 y₌e^x

 

 

 

                                                                          1

                            

    √-2         0               √2                                   0              3

   

                   

 

 

                         Інтерактивна гра «Хто швидше»

 

Учні об’єднуються для роботи в групи.

Вчитель пропонує групам картку із завданням і дає на обмірковування відповіді  1 хв.

Група, яка першою дасть правильну відповідь, одержує по 1 балу за кожне завдання.

 

Картка для роботи групи

 

1. Обчисліть інтеграл:

 

 

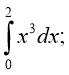
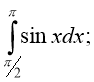
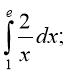
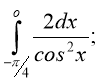
а)                        б)                          в)                    г)

 

 

 

                                            

 

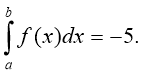
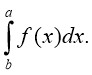
2. Відомо, що                              Знайдіть                                 

 

 

 

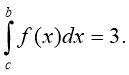
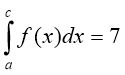
3.  Відомо, що                       ,                            Знайдіть

 

  

4.                 Удосконалення знань, умінь і навичок.

 

Виконання письмових вправ.

 

Обчисліть інтеграл:

                            

 

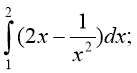
1)                                 2)                                   3)

 

                                                                                   

  

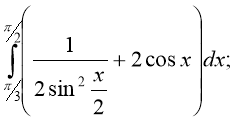
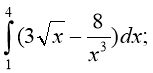
4)                                 5)                            6)    

 

 

 

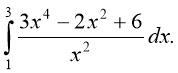
7)                                                                    

 

 

Приклади обчислення площ криволінійних трапецій:

 

Приклад 1. Обчисліть площу криволінійної трапеції, обмеженої графіком функції у=х² +1 та прямими у=0, х=1, х=4

 

 

  Розв’язання:                                                                     у=х²+1

                                                                                

 S =

 

 

 

 

 

 

 

 

 

 

 

Приклад 2. Обчисліть площу криволінійної трапеції,

обмеженої графіком функції у= 9 - х² та прямою у=0.

 

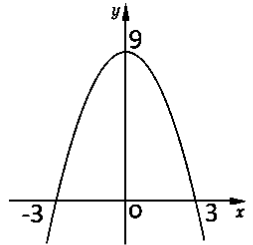
Розв’язання:

 

Знайдемо точки, у яких парабола  у=9-х²                                 у=9-х² 

перетинає вісь                                                                                             

абсцис:  9 - х² = 0, х₁=-3, х₂=3 

 

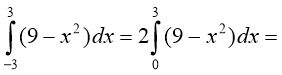
S =

 

 

 

 

Приклад 3. Обчисліть площу фігури, обмеженої прямими х=1, х=8, віссю ох і графіком функції у=.

 

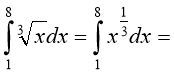
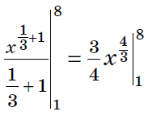
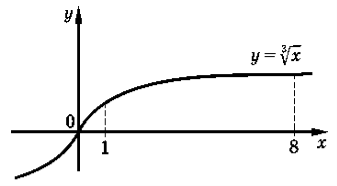S =                                            

 

                                            

 

 

 

 

 

 

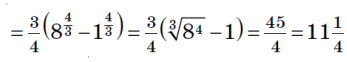
Картка для роботи групи

 

1. Обчисліть інтеграл:

 

 

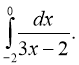
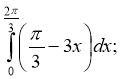
    а)                            б)

 

 

2. Знайдіть площу фігури, обмеженої лініями у=sinx, y = 0, x= 0, x=.

 

3. Знайдіть площу фігури, обмеженої лініями у=,  у=0, х=1, х=4.

 

4. Знайдіть площу фігури, обмеженої лініями у=4 - х² та прямою у=0.

                                                                         

                                                                           

5.  Застосування знань, умінь і навичок.

 

Самостійна робота

 

Варіант 1

 

 

У завданнях 1–3 позначте правильну, на вашу думку, відповідь.

1. Які із заштрихованих фігур, зображених на рисунках, є криволінійними трапеціями?

 

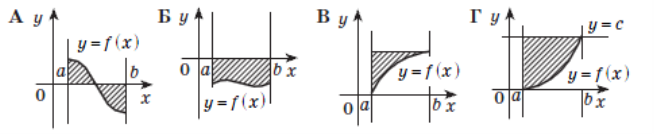
2. Виберіть криволінійну трапецію, обмежену графіками функцій

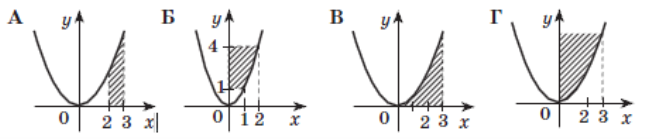y = x², y = 0, x = 2, x = 3.

 

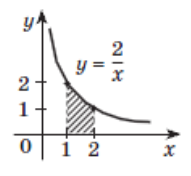
3. Укажіть вираз для знаходження площі

фігури, зображеної на рисунку, за

допомогою інтеграла.

 

 

 

 

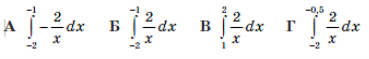
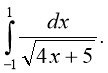
4. Обчисліть інтеграл                                                            

 

 

 

 

                                                                                                           

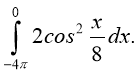
5. Обчисліть інтеграл                                                            

 

 

 

 

 

Варіант 2

 

У завданнях 1–3 позначте правильну, на вашу думку, відповідь.

1. Які із заштрихованих фігур, зображених на рисунках, є криволінійними трапеціями?

 

 

 

 

 

 

 

 

 

 

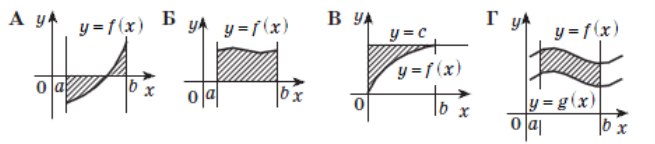
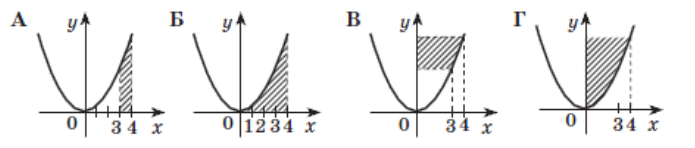
2. Виберіть криволінійну трапецію, обмежену графіками функцій

y = x², y = 0, x = 3, x = 4 та обчисліть площу.

 

 

 

 

 

 

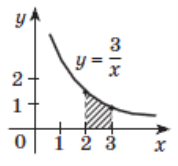
3. Укажіть вираз для знаходження площі

фігури, зображеної на рисунку, за

допомогою інтеграла.

 

 

 

                         

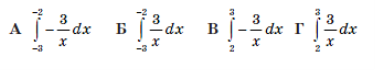
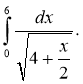
4. Обчисліть інтеграл                                                          

 

 

 

 

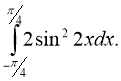
5. Обчисліть інтеграл                                                            

 

 

 

VI. Домашнє завдання.

 

Повторити  § 8-12;  розв’язати самостійну роботу №2 ст.116 ( по підручнику ).