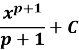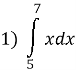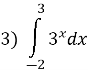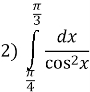Урок. Визначений інтеграл. Його геометричний зміст. Формула Ньютона-Лейбніца.
Тема: Визначений інтеграл. Його геометричний зміст. Формула Ньютона – Лейбніца.
Мета уроку:
засвоїти означення площі криволінійної трапеції, навчитися знаходити площу криволінійної трапеції; розглянути означення визначеного інтеграла та навчитися знаходити визначений інтеграл; засвоїти формулу Ньютона-Лейбніца та розглянути геометричний зміст визначеного інтеграла;
розвивати вміння знаходити площу криволінійної трапеції та визначений інтеграл;
виховувати інтерес до вивчення точних наук; вміння правильно висловлювати свою думку.
Цілі:
домогтися засвоєння формули Ньютона-Лейбніца;
навчитися обчислювати площі криволінійних трапецій, застосовуючи дану формулу;
Формувати:
математичну компетентність (застосовувати нові означення до розв’язування задач)
комунікативну компетентність (спроможність грамотно висловити свою думку)
інформаційну компетентність (спроможність опрацьовувати нові пізнавальні дані)
загальнонавчальну компетентнісь (спроможність організовувати власну діяльність під час виконання завдань)
Тип уроку: засвоєння нових знань;
Хід уроку
- Організаційний етап
- Перевірка домашнього завдання
На мультимедійній дошці подано розв’язки завдань, учні шляхом взаємоперевірки виправляють допущені помилки.
- Актуалізація опорних знань
- Що ми називаємо інтегруванням функції?
- Сформулюйте означення первісної функції
- Сформулюйте основну властивість первісної
- Що ми називаємо невизначеним інтегралом?
Пригадаємо таблицю первісних
|
Функція |
Первісна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- Мотивація навчальної діяльності
Слово вчителя.
Розглянемо задачу: Автомобіль рухається по прямій зі швидкістю v0 км/год .
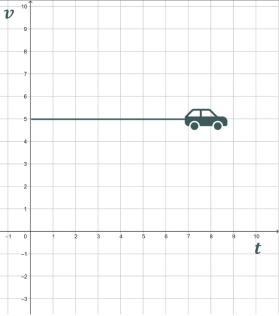
Як знайти шлях, що подолає автомобіль?
![]()
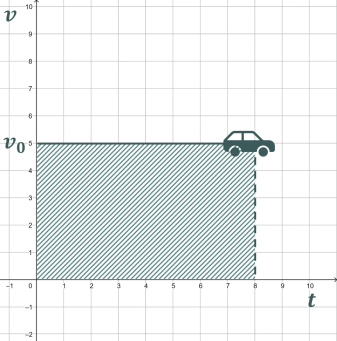
Чи буде цей шлях дорівнювати площі ![]() прямокутника?
прямокутника?
(Так)
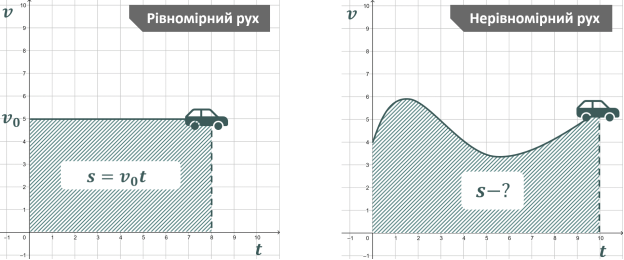
Проблемне питання:
Чи можемо знайти площу такої фігури?
- Вивчення нового матеріалу.
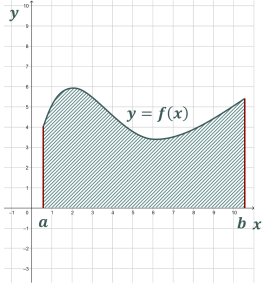 Означення
Означення
Якщо функція ![]() неперервна на проміжку
неперервна на проміжку ![]() і
і ![]() , то фігура, обмежена графіком функції
, то фігура, обмежена графіком функції ![]() і прямими
і прямими ![]() , називається криволінійною трапецією.
, називається криволінійною трапецією.
*Відрізок ![]() – це основа криволінійної трапеції.
– це основа криволінійної трапеції.
Приклади криволінійних трапецій:
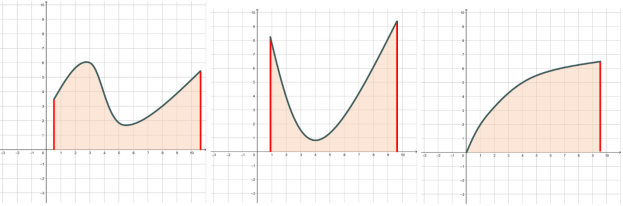
- Площа криволінійної трапеції

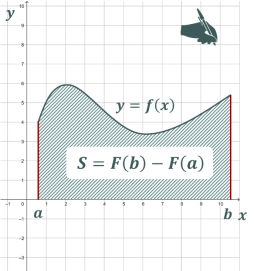
Теорема
Площу ![]() криволінійної трапеції, обмеженої графіком функції
криволінійної трапеції, обмеженої графіком функції ![]() і прямими
і прямими ![]() і
і ![]() можна обчислити за формулою
можна обчислити за формулою
![]() , де
, де ![]() будь-яка первісна функції
будь-яка первісна функції ![]() на проміжку
на проміжку ![]()
Наприклад:
Знайдіть площу криволінійної трапеції, обмеженої відрізками
![]() , віссю
, віссю ![]() і графіком функці
і графіком функці ![]() .
.
Розв’язок:
Назвіть одну з первісних ф-ї ![]() на проміжку
на проміжку ![]()
![]()

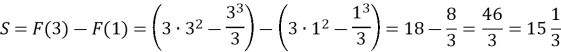
- Формула Ньютона-Лейбніца
Означення
Нехай ![]() – первісна функції
– первісна функції ![]() на проміжку
на проміжку ![]() , числа
, числа ![]() , належать проміжку
, належать проміжку ![]() . Різницю
. Різницю ![]() називають визначеним інтегралом функції
називають визначеним інтегралом функції ![]() на проміжку
на проміжку ![]()
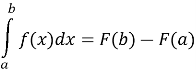
Числа ![]() – це межі інтегрування:
– це межі інтегрування: ![]() – нижня межа,
– нижня межа, ![]() – верхня межа.
– верхня межа.
*Отримана рівність називається формулою Ньютона-Лейбніца
- Геометричний зміст визначеного інтеграла
Використовуючи теорему про площу криволінійної трапеції та формулу Ньютона-Лейбніца можна зробити висновок, що площа криволінійної трапеції, обмеженої графіком неперервної і невід’ємної на відрізку ![]() функції
функції ![]() , відрізком
, відрізком ![]() осі
осі ![]() і прямими
і прямими ![]() і
і ![]() , можна обчислювати за формулою
, можна обчислювати за формулою
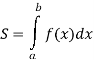
Сформулюйте теорему про площу криволінійної трапеції
![]()
Сформулюйте формулу Ньютона-Лейбніца
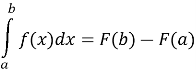
Який можемо зробити висновок?

Ця формула виражає геометричний зміст визначеного інтеграла.
- Обчислення визначеного інтеграла
-
Знайти будь-яку первісну
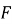 функції
функції  на проміжку
на проміжку 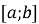 ;
;
-
Обчислити значення первісної
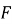 у точках
у точках 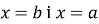 ;
;
-
Знайти різницю
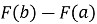 ;
;
Виконуючи обчислення визначених інтегралів зручно використовувати такий запис:
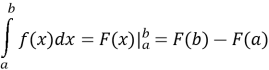
Наприклад:
Знайдіть площу криволінійної трапеції, обмеженої відрізками
![]() , віссю
, віссю ![]() і графіком функції
і графіком функції ![]()
Розв’язок:
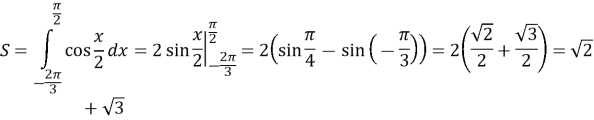
- Засвоєння нових знань та вмінь учнів
№1
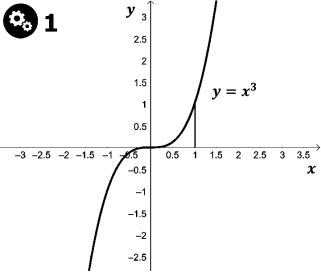
Знайдіть площу криволінійної трапеції, зображеної на рисунку:


Маємо криволінійну трапецію, яка обмежена графіком функції
![]() і прямими
і прямими ![]() .
.
Знайдемо первісну:
![]()
За теоремою про площу криволінійної трапеції знайдемо площу:
![]()

Маємо криволінійну трапецію, яка обмежена графіком функції
![]() і прямими
і прямими ![]() .
.
Знайдемо первісну:
![]()
За теоремою про площу криволінійної трапеції знайдемо площу:
![]()

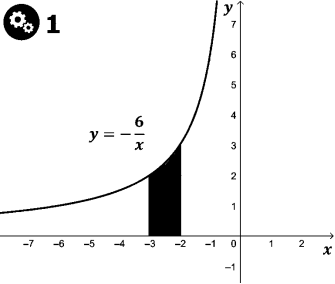 Маємо криволінійну трапецію, яка обмежена графіком функції
Маємо криволінійну трапецію, яка обмежена графіком функції
![]() і прямими
і прямими ![]() і
і
![]() .
.
Знайдемо первісну:
![]()
За теоремою про площу криволінійної трапеції знайдемо площу:
![]()
№2
Обчисліть визначений інтеграл:
|
|
|
|
|
|
Розв’язання:

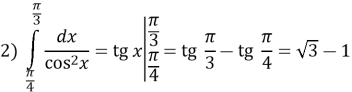
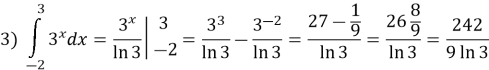
№3
Знайдіть площу криволінійної трапеції, обмеженої:


-
Ппараболою
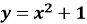 і прямими
і прямими 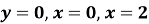
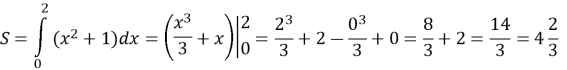
Відповідь: ![]()

-
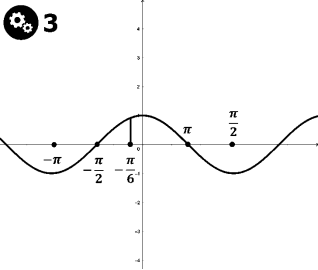
Косинусоїдою
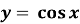 і прямими
і прямими
![]()
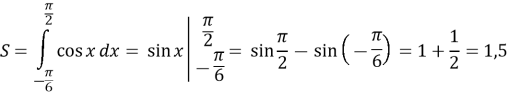
Відповідь: ![]()
№4
Обчисліть визначений інтеграл:

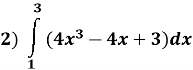
Розв’язання:
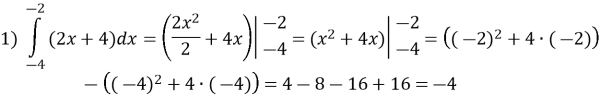
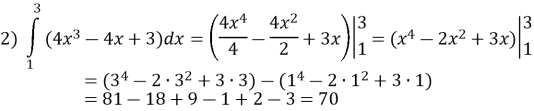
№5
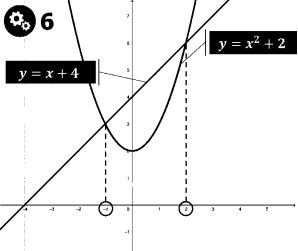
Знайдіть площу фігури, обмеженої лініями:
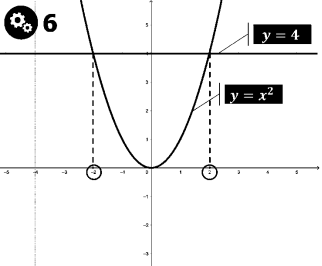 Розв’язання:
Розв’язання:
ЯЯких даних нам не вистачає для знаходження площі фігури?
(Потрібно знайти межі інтегрування)
 Ммежі інтегрування – це абсциси точок перетину графіків даних функцій. Отже, якщо
Ммежі інтегрування – це абсциси точок перетину графіків даних функцій. Отже, якщо ![]()
Які є ідеї для знаходження цієї площі?
(Учні висловлюють свої ідеї)
Розв’язання:
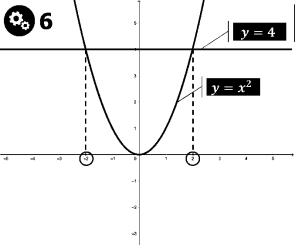
 Знайдемо площу квадрата утвореного віссю
Знайдемо площу квадрата утвореного віссю ![]() , прямою
, прямою ![]() та
та ![]() ,
, ![]()

Віднімемо від знайденої площі квадрата площу криволінійної трапеції утвореної графіком ![]() , віссю
, віссю ![]() та прямими
та прямими ![]() ,
, ![]()

Відповідь: ![]()
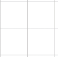
Як можемо знайти площу зафарбованої фігури?
(Площа зафарбованої фігури дорівнює різниці площ криволінійної трапеції, утвореної графіком функції ![]() , віссю
, віссю ![]() , прямими
, прямими ![]() ,
, ![]() та криволінійної трапеції утвореної графіком функції
та криволінійної трапеції утвореної графіком функції ![]() , віссю
, віссю ![]() та прямими
та прямими ![]() ,
, ![]() )
)
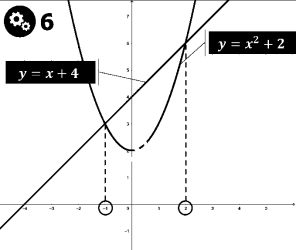
Як можемо знайти площу ![]() ?
?

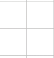
Як можемо знайти площу ![]() ?
?
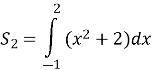
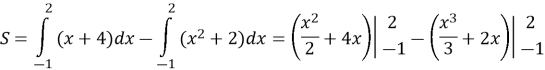
![]()
![]()
Відповідь: ![]()
- Підведення підсумків уроку
Рефлекція
На уроці …
Я дізнався…
Я навчився …
Я зможу …
Цей урок мені запам’ятався…
Я хотів би …
- Домашнє завдання
Опрацювати §10
Виконати № 10.4; 10.6; 10.10; 10.12
Істер О.С.


про публікацію авторської розробки
Додати розробку