Сума n-перших членів арифметичної прогресії

Сума n-перших членів арифметичної прогресії

Мета: формувати дослідницьку, процедурну та методологічну компетентності; активізувати знання учнів про арифметичну прогресію, формули для знаходження n-го члена прогресії, вивести формулу S_n для арифметичної прогресії; формувати  вміння використовувати на практиці алгоритм розв’язання типових задач та аналізувати ефективність їх розв’язання  математичними методами; формувати самостійність, розвивати системність і послідовність мислення; виховувати розуміння ролі математики у житті та важливості математичних знань.

Хід уроку

І. Актуалізація опорних знань

Прогресії є відображенням світу, що нас оточує. Найдавнішою задачею на прогресії є задача про розподіл хліба, записана в єгипетському папірусі Рінда, яка відноситься до ІІІ ст. до н.е.

Бачимо, що перші із задач на прогресії, які дійшли до нас, пов’язані із запитами господарського життя і суспільної практики, як, наприклад, розподіл продуктів та спадщини, одержання винагороди.

 А де ще застосовується прогресія? ( в таких науках, як:

- фізика: під час вивчення тіл, що вільно падають чи рухаються рівноприскорено, під час вивчення процесу радіактивного розпаду;

- економіка та банківська справа: під час виплати відсотків та надання кредитів;

- у техніці: під час виготовлення обладнання.

Отже, ми розуміємо актуальність того, над чим працюємо, важливість теми, що вивчається. Сьогодні на уроці ми доповнимо і закріпимо ваші знання з вивченої теми. Результати вашої роботи перш за все будуть залежати від настрою на цей урок та бажання зрозуміти матеріал для успішного виконання завдань ДПА, ЗНО.. Нехай він пройде під девізом: «Переконай себе в тому , що арифметичну прогресію необхідно зрозуміти і навчитися застосовувати»

Кінезіологічна вправа. Для налаштування на плідну роботу сядьте рівно, покладіть одну долоню на лоба, а іншу – на потилицю. Потім заплющіть очі, сконцентруйтесь на  занятті та зробіть кілька глибоких вдихів – видихів. Готові до роботи?

До запропонованих вправ поставте запитання і нехай однокласники дадуть на них відповіді

1) -5; -3; -1; 1; …

2) 2; 5; 8; 13;…;

2) α₁ = -0,5, d = 2;

3) α₁₅=  -4,      α₁₇=  -8;

4) α₇= -6,5;         α₈= -8,5.

Ми пригадали означення арифметичної прогресії  та формулу для знаходження n-го члена арифметичної прогресії, а зараз пропоную по групах провести обчислення суми чисел а) від 11 до 20; б) від 40 до 49; в) від 1 до 50. Обчислення проводимо якомога зручніше і швидко. (Відповіді а)155; б) 445; в)1275).

ІІ. Формулювання мети й завдань уроку

Як ви проводили обчислення? Яку  властивість скінченної арифметичної прогресії ви помітили та, можливо використали для встановлення формули суми n перших її членів ?

(Сума будь-яких двох її членів, рівновіддалених від крайніх членів, дорівнює сумі крайніх членів) То хто спробує вивести формулу суми n перших її членів ?

S_n = a₁ +a₂ + … +a_n-1 +a_n

S_n = a_n+a_n-1 +… + a₂ +a₁

2S = (a₁ +a_n) + (a₂ + a_n-1) + (a₃+a_n-2) + …(a_n-1 +a₂) + (a₁ + a_n)

де а₂ + a_n-1 = a₁ +d + a_n -d = a₁ +a_n

2S_n = (a₁ + a_n) ∙ n

S_n = ∙ n

Ми маємо ще формулу n-го члена арифметичної прогресії. Спробуйте її застосувати

S_n =

В якому випадку і яку формулу зручно застосовувати?

Незважаючи на те, що задачі на прогресії були відомі протягом 50 століть, у шкільних підручниках прогресії з’явилися порівняно недавно. Так, у підручнику Л.Магницького, виданого 200 років тому, прогресії хоча і є, але загальних формул, які пов’язують величини між собою, в ньому не наведено. Між тим формули суми членів арифметичної прогресії можна легко вивести простим і наочним способом з допомогою паперу у клітинку. На такому папері будь-яку арифметичну прогресію можна зобразити східчастою фігурою.

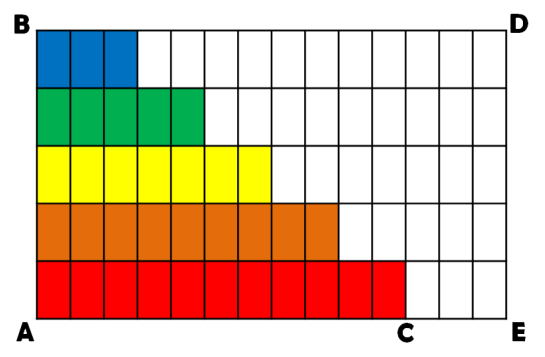
Фігура на даному малюнку зображую прогресію: 3, 5, 7, 9, 11,…

Щоб визначити суму її членів доповнимо креслення до прямокутника. Одержимо дві рівні фігури. Площа кожної з них зображує суму членів нашої прогресії.

Отже, S_n = (AC + CE) ∙ AB

Але AC + CE зображає суму першого і п’ятого членів, АВ – кількість членів прогресії.

Тому, 2S = (сума крайніх членів) ∙ (кількість членів)

S_n = ∙ n

Це моделювання може допомогти  вам згадати формулу суми n перших  членів арифметичної прогресії в будь-якій ситуації, наприклад на  ДПА.

Кінезіологічна вправа. Вправу можна виконувати стоячи або сидячи.

• голову тримати прямо, але шия та підборіддя мають бути розслаблені;
• треба взятися за вуха так, щоб великий палець опинився з тильного боку, а всі інші попереду;
• виконувати масаж зверху до низу, а дійшовши до мочки, м’яко масажувати і її;
• повторити 4 рази.

ІІІ. Застосування вивчених формул до розв’язування задач

1. В інструкції з медичного застосування настою лікарської рослини зазначено, що його рекомендовано приймати щоденно упродовж 20 діб. Протягом першої доби пацієнт має випити 370 мл настою, а кожної наступної доби - на одну й ту саму кількість настою менше, ніж попередньої. Останньої доби прийом має становити 85 мл цього лікарського засобу. Яку кількість настою (у мл) випє пацієнт за ці 20 діб, якщо дотримуватиметься інструкції? (ЗНО 2015)

Розв’язання

n = 20.  

a₁ = 370 мл.

a₂₀ = 85 мл.

S₂₀ = =

4550 мл.

2. Робітники отримали замовлення викопати криницю. За перший викопаний у глибину метр криниці їм платять 50 грн, а за кожний наступний – на 20 грн більше, ніж за попередній. Скільки грошей (у грн) сплатять робітникам за викопану криницю завглибшки 12 м? (ЗНО 2010)

Розв’язання

α₁ = 50 грн;

d = 20 грн; 

S₁₂ = =

= =

= (100 + 220) 6 = 320 6 = 1920 (грн)

3. Плавець під час першого тренування подолав дистанцію у 450 м. Кожного наступного тренування він пропливав на 50 м більше, ніж попереднього, поки не досягнув результату 1000 м за одне тренування. Після цього під час кожного відвідування басейну плавець пропливав 1000 м. Скільки всього кілометрів плавець проплив за перші 10 тижнів тренувань, якщо він тренувався тричі кожного тижня?

Розв’язання

a₁ = 450 м.

d = 50 м.

a_n = 1000 м.

a_n = a₁ + d (n - 1)

1000 = 450 + 50 (n – 1)

n – 1 = = 11

n = 12

Перші чотири тижні.

S = 8700 (м).

За 6 тижнів по 3 тренування:

3 1000 6 = 18000 м.

18000 + 8700 = 26700 м.

№ 17.9 (1). Знайдіть суму дванадцяти перших членів арифметичної прогресії (а_n), якщо а₁ = 6, а₉ = 22.

Розв’язання

а₉ = a₁ + 8d

22 = 6 + 8d

8d = 16

d = 2

= 204

ІV. Підведення підсумків

На цьому етапі визначити, чи досягнуті мета, очікувані результати уроку, провести рефлексію. Учням пропонується дати відповіді на запитання таблиці. Листи самооцінювання здаються вчителеві, який підбиває підсумок уроку, оголошує оцінки.

Таблиця для рефлексії

	Так	Не добре	Ні
Я знаю і розумію: Що таке арифметична прогресія Різниця арифметичної прогресії Зростаюча та спадна АП
Я вмію: Знаходити різницю d Знаходити суму АП n-ий член АП
Я вчився сам: Пояснювати, щоб всі зрозуміли Розуміти пояснення іншого Не відволікатись Не заважати іншим Я досягну успіху!!!

 

Я дякую вам за роботу на уроці. І хочу побажати вам постійного росту знань як зростає нескінченна арифметична прогресія і нехай оцінювання буде різницею більше 0. А тепер і ви побажайте один одному використовуючи означення та властивості арифметичної прогресії.

V. Домашнє завдання

Опрацювати п.17, №17.6, №17.10.

Продовжити роботу з завданнями ЗНО.

Завдання ЗНО. Арифметична прогресія

1. В арифметичній прогресії (