Урок «Застосування похідної до розв’язування прикладних задач»
Тема уроку: «Застосування похідної до розв’язування прикладних задач»
Задачі уроку:
- продовжувати формувати навички застосування формул і правил диференціювання при розв’язуванні вправ;
- формувати уміння застосувати знання та способи дій у нових навчальних ситуаціях, на практиці;
- розвивати вміння логічно мислити, аналізувати, робити висновки;
- виховувати відповідальність за свою роботу, почуття колективізму під час розробки та виконання проекту.
Очікувані результати:
- учні закріплять свої знання та вміння для обчислення похідної;
- знатимуть історію її виникнення;
- вмітимуть пояснити застосування похідної у різних галузях науки та на практиці.
Обладнання: екран, мультимедійний проектор, презентація до уроку.
Тип уроку: комбінований (з використанням проектів).
Епіграф уроку: «Не достатньо мати лише добрий розум, головне – це раціонально застосовувати його» Р.Декарт.
План уроку.
|
№ з/п |
Назва етапу уроку |
Методи та прийоми |
|
1 |
Мотивація навчальної діяльності |
Проблемне питання (відео фрагмент) |
|
2 |
Актуалізація опорних знань |
1.Повідомлення учнів 2.Тест – допуск 3.Математичне лото |
|
3 |
Фізкультхвилинка |
Відео ролик |
|
4 |
Закріплення вмінь і навичок |
Захист проектів |
|
5 |
Оцінювання учнів |
1.Заповнення картки самоконтролю 2.Заповнення картки залікового рейтингу |
|
6 |
Підсумки уроку |
1.Розв’язання проблемного питання 2. «Незакінчене речення» |
|
7 |
Домашнє завдання |
|
Хід уроку.
1.Мотивація навчання.
Учитель: Сьогодні проведемо з вами ділову гру під назвою “Компетенція”. Виникає запитання: а що ж це означає?
Компетенція – коло питань, у яких дана особа має знання, досвід.
Компетентний (з латинської - “здатний”, “відповідний”) - це той, хто вміє застосовувати набуті знання та досвід.
Усе людське життя — це не що інше, як бажання досягти успіху в розв'язуванні все нових питань та проблем. Для цього,звичайно, необхідно бути розумною, освіченою, компетентною людиною. Стати такою можна тільки тоді, коли розум не знає ні хвилини спокою, а силу розумові додають вправи і постійний пошук.
Наш сьогоднішній урок — теж пошук, пошук шляхів досягнення успіху, бо тільки компетентна людина може досягти успіху.
Я сподіваюсь, що сьогодні ми з вами успішно попрацюємо і всі будуть задоволені від зустрічі на цьому уроці.
Досягти успіху можна тільки тоді, коли є певна мета. Мета сьогоднішнього уроку для вас така: ви повинні показати раціональне використання свого розуму при удосконаленні своїх компетенцій за час вивчення теми «Похідна».
Увага на екран (відео фрагмент «проблема»).
Відповідь на це питання ми спробуємо дати в кінці уроку.
2. Актуалізація опорних знань.
Учитель: Шановні одинадцятикласники! Уміння працювати самостійно є дуже важливим і в навчанні, і в житті. Але, крім того, для досягнення успіху в житті потрібно мати друзів, партнерів. Тому під час роботи на уроці дозволяється здійснювати взаємодопомогу. Ви розділені на групи. У кожній групі є свій «спонсор знань», який зможе упродовж уроку надавати вам допомогу, а ваші досягнення я фіксуватиму в «картках залікового рейтингу».
А зараз послухаємо повідомлення, підготовлені нашими «спонсорами знань» за матеріалами додаткової літератури.
2.1. Повідомлення учнів.
Повідомлення I учня - «Шлях Дідони»
Повідомлення II учня – «Похідна у фізиці й техніці»
Повідомлення III учня – «З історії похідної»
Учитель. Ви побачили багатогранність використання похідної у фізиці та техніці і переконалися, що математика не тільки «цариця», але й «служниця» інших наук.
2.2. Тест – допуск.
Учитель: Щоб продовжити наш урок, потрібно згадати вивчений раніше матеріал. Для цього вам роздано картки з завданнями, які ви повинні виконати.
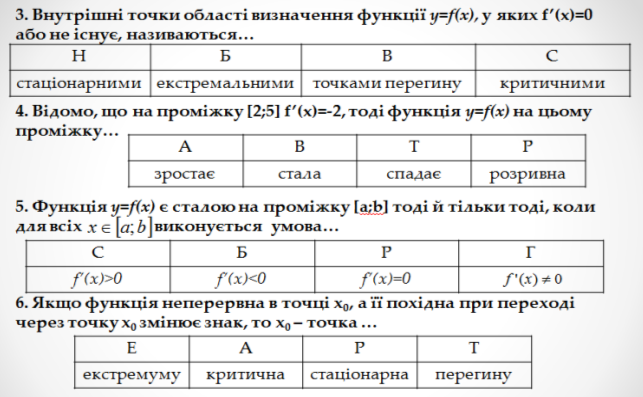
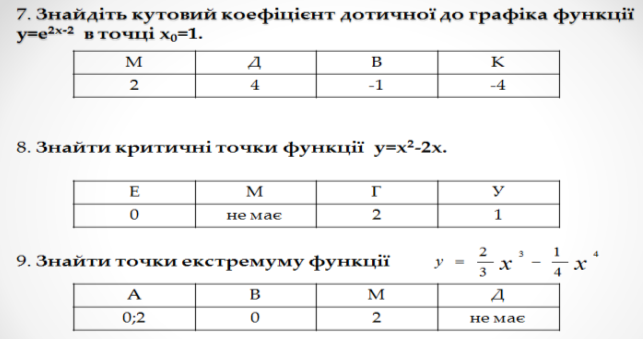
Учитель: Запишіть букви вибраних варіантів відповідей в одну строчку.
Якщо завдання виконано вірно, то отримаєте слово ЕКСТРЕМУМ.
2.3. Математичне лото.
Учитель: Продовжимо визначення вашої компетентності за допомогою математичного лото. Для цього виконайте завдання, записане на картці.
3. Фізкультхвилинка (проектується на екран).
Учитель: Ви добре попрацювали, і для подальшої роботи потрібно трішки відпочити та розім’яти м’язи.
4. Закріплення вмінь і навичок.
Учитель: А зараз надаємо слово групам для захисту проектів « Похідна в прикладних задачах».
4.1. Проект І групи.
Визначити висоту басейну із квадратним дном, об’єм якого 32 м3, такого, щоб на облицювання його стін і дна, витрати на матеріали були найменшими.
|
Розв’язування
Нехай довжина та ширина басейну – |
|
Відповідь: 4 м. |
4.2. Проект ІІ групи.
Задача – проблема: «Яку з чашок вигідніше купляти?». Звісно дешевшою є та, на яку іде менше матеріалу. Для цього дослідимо чашки циліндричної форми. Математично задача звучить так: який із циліндрів з периметром осьового перерізу Р має найбільшу бічну поверхню?
|
Розв’язування.
Відомо, що Sб = 2πRH, а периметр осьового перерізу P = 2(H+2R) = 2H+4R. Нехай R = x, тоді 2H = P - 4x і H = Отже, функцію f(x) = πРх - 4πх2 дослідимо на екстремум.
f ʹ (x) = πР - 8πх. Розв’язуємо рівняння πР - 8πх = 0. Маємо х =
відповідно Н = =
|
|
|
5. Оцінювання учнів.
Учитель: Настав час кожному з вас дати оцінку своїй роботі на уроці. У вас є «картка самоконтролю». Заповніть її, об’єктивно оцінивши свої досягнення на уроці.
5.1. Заповнення картки самоконтролю
Картка самоконтролю
Прізвище та ім'я учня _________________________
Оцініть себе (від 0 до 2 балів) за кожним із визначених напрямків
1. Ви брали активну участь у проектній роботі групи _____ .
2. Ви вносили вдалі пропозиції, які були враховані в ході розв'язування задач _.
3. Ви виконували розрахунки проекту _____ .
4. Ви захищали проект _____.
5. Ви засвоїли навчальний матеріал _____ .
6. Ви брали активну участь в обговоренні проектів на уроці _______.
Усього балів ________
5.2. Заповнення картки залікового рейтингу (заповнює вчитель протягом уроку).
Картка залікового рейтингу учнів з теми
«Застосування похідної до розв’язування прикладних задач»
|
№ з/п |
Прізвище, ім’я учня |
Вид роботи, максимальна кількість балів. |
||||||
|
тест - допуск |
математичне лото |
домашній проект |
самоконтроль |
робота на уроці |
всього балів |
оцінка |
||
|
12 |
12 |
12 |
12 |
12 |
60 |
12 |
||
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
Шкала оцінювання
|
Кількість балів |
1-5 |
6-10 |
11-15 |
16-20 |
21-25 |
26-30 |
31-35 |
36-40 |
41-45 |
46-50 |
51-55 |
56-60 |
|
Оцінка |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
6. Підсумки уроку.
Учитель: Наш урок добігає кінця. Кожен з вас показав і оцінив свою компетентність з теми «Похідна». Тож підведемо підсумки сьогоднішнього уроку.
6.1. Розв’язання проблемного питання.
Заслуховуються відповіді учнів. Потім проектується відео ролик на екран («проблема_відповідь»).
Учитель: А зараз я пропоную вам самим підвести підсумок вашої роботи на уроці, доповнивши незакінчені речення.
6.2. «Незакінчене речення».
Закінчіть наступні речення:
- Під час проведення уроку мені сподобалося …
- Під час проведення уроку мені не сподобалося …
- Найскладнішим для мене було …
- Мені сподобалося працювати у групі, тому що …
- Я проявив (розвинув у собі) такі якості, як …
- Я добре виконав …
-
Домашнє завдання:
Підручник: Є.П.Нелін «Алгебра» 11 клас, Харків, «Гімназія», 2011 р., академічний рівень.
Початковий рівень: повторити §2, виконати впр.6 (стор. 29).
Середній рівень: повторити §2,3, виконати впр.1,2 (стор. 39).
Достатній рівень: повторити §2-4, виконати впр.10 (стор. 45),
впр.14(2) (стор. 66).
Високий рівень: повторити §2-5, виконати впр.3(1-3) (стор. 90),
скласти кросворд на тему «Похідна».
1
Цікавою є легенда про відшукування найбільшого значення функції, за якою засновниця м. Карфагена Дідона, дочка царя тірів, посварившись з братом Пігмаліоном, втекла від свого батька і після багатьох пригод з'явилася на південному узбережжі Середземного моря. Тут, у царя Нарбаса, за невеликі гроші вона купила шматок землі «не більше, ніж можна обміряти шкурою бика» - як зазначалося в угоді. Місцеві жителі вважали умову буквальною і розраховували, що Дідоні для нового поселення дістанеться дуже маленький клаптик узбережжя. Проте спритна Дідона розрізала шкуру бика на найтонші смужки, зв'язала їх мотузкою і, закріпивши один її кінець на березі моря, пішла з іншим вздовж берега.
Перед нею постало питання: яку форму потрібно надати мотузці, щоб «обміряти шкурою бика» найбільшу площу? Зокрема, це є задача на пошук замкненої кривої даної довжини, що обмежує найбільшу площу. Виявляється, що такою кривою є коло . Дідоні, щоб розв'язати задачу потрібно було обійти півколо з центром у точці О. На ділянці землі, яку вона відміряла, й було засновано місто Карфаген. Карфаген
Поняття похідної виникло у XVII столітті у зв'язку з необхідністю розв'язати деякі математичні і фізичні задачі. Задачу про побудову дотичної розв'язав Г. Лейбніц. Про визначення миттєвої швидкості під час прямолінійного нерівномірного руху – І. Ньютон, який прийшов до поняття похідної, виходячи з положень механіки. Похідна – це швидкість зміни функції. Нехай матеріальна точка рухається вздовж координатної прямої х за законом x=x(t). Тоді похідна від координати за часом у даний момент є швидкістю руху в цей момент часу. У цьому полягає її механічний зміст. Поняття похідної як швидкості зміни функції використовується під час означень багатьох фізичних величин. Наприклад, похідна швидкості руху за часом є прискорення; похідна величини заряду за часом є сила струму; похідна потоку магнітної індукції за часом є електрорушійна сила індукції; похідна роботи за часом є потужність. Готфрід ЛейбніцІсаак Ньютон
До відкриття похідної незалежно один від одного прийшли два відомих учених – І. Ньютон і Г. Лейбніц наприкінці XVII століття. Проте, ще задовго до цього Архімед розв'язав задачу на побудову дотичної до кривої та знайшов максимум функції f(x)=x2(a-x). Різні задачі, що пов'язані з поняттям похідної, зустрічалися у працях Н. Тартальї, М. Кеплера, Р. Декарта. І. Ньютон сформулював і розв'язав основну проблему математичного аналізу: « За даною довжиною шляху в будь-який момент часу знайти швидкість руху у вказаний час». І якщо він виходив із задач механіки, то Г. Лейбніц – із геометричних задач. У Г. Лейбніца первісним поняттям була дотична, а у І. Ньютона – швидкість. Швидкість зміни функції f(x) у точці х0 називається похідною функції f(x) у точці х0. Архімед. Нікколо Тарталья. Йоган Кеплер. Рене Декарт
про публікацію авторської розробки
Додати розробку