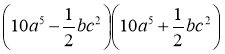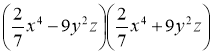Формули скороченого множення

Варіант 1

Варіант 2

1°. Перетворіть вираз у многочлен:

l) (а + 7)²;

2) (m – 6)(т + 6);

3) (3x – 4у)²;

5) (5а + 8b)(8b – 5а);

6) .

1°. Перетворіть вираз у многочлен:

1) (с – 6)²;

2) (5 – а)(5 + а);

3) (2а + 3b)²;

4) (a – 1)(а² + а + l);

5) (7х + 10у)(10у – 7х);

6) .

2°. Розкладіть на множники:

1) 25х² – 16;      2) 9х² – 12ху + 4у²;

3) т³ + 27п³;     4) 0,001х⁶ – 1.

2°. Розкладіть на множники:

1) 100 – 9х²;     2) b³ – 8с³;

3) 4а² + 20аb + 25b²;  4) 0,125х³ – 8.

3°. Спростіть вираз:

1) (х – 3)² – (х – 1)(х – 4) + (х – 2)(х + 2);

2) (х – 2)(х² + 2х + 4) – х(х – 3)(х + 3).

3°. Спростіть вираз:

1)(х + 5)² – (х – 4)(х + 4) + (х – 3)(х + 7);

2) (2 + у)(у² – 2у + 4) – (у – 2)у(у + 2).

4*. Розв'яжіть рівняння:

1) (2у – 3)(3у + 1) + 2(у – 5)(у + 5) = = 2(1 – 2у)² + 6у;

2) (3х – 7)² – 4х² = 0.

4*. Розв'яжіть рівняння:

1) 4(3у + 1)² – 27 =

= (4у + 9)(4у – 9) + 2(5у + 2)(2у – 7);

2) (8у – 1)² – 49у² = 0.

5*. Доведіть, що вираз х² – 4х + 5 набу­ває лише додатних значень при будь-яких значеннях х.

5*. Доведіть, що вираз х² – 14х + 51 на­буває лише додатних значень при будь-яких значеннях х.

6**. Спростіть вираз

(а² + а + 1)(а⁶ + 1)(а²⁴ + 1) ×

× (a + l)(а¹² + 1)(a² – a + l)(a – 1)

6**. Спростіть вираз

(a² – a + l)(а⁶ + 1)(a + l) ×

× (a¹² + 1)(a – 1)( a² + a + l)(а⁴ + 1)

Варіант 1

Варіант 2

1°. 1) а² + 14а + 49; 2) m² – 36;

      3) 9х² – 24ху + 16у²; 4) у³ + 1;

      5) 64b² – 25а²; 6)100а¹⁰ - b²с⁴.

1°. 1) c² – 12c + 36;  2) 25 – a²;

      3) 4a² + 12ab + 9b²;  4) a³ – 1;

      5) 100y² – 49x²; 6) x⁸ – 81y⁴z².

2°. 1) (5х – 4)(5х + 4); 2) (3х – 2у)²;

      3) (т + 3п)(т² – 3тп + 9п²);

      4) (0,1х² – 1)(0,01х⁴ + 0,1х² + 1).

2°. l) (10 – 3x)(10 + 3x);

      2) (b – 2c)(b² + 2bc + 4c²);

      3) (2a + 5b)²;

      4) (0,5x – 2)(0,25x² + x + 4).

3°. 1) х² – 6х + 9 – х² + 5х – 4 + х² – 4 =

           = х² – х + 1;

      2) х³ – 8 – х³ + 9х = 9х – 8.

3°. 1) x² + 10х + 25 – x² + 16 + x² + 4x – 21 =

         = x² + 14x + 20;

      2) 8 + у³ – у² + 4у = 4у + 8.

4*. 6у² – 7у – 3 + 2у² – 50 =

      = 2 – 8у + 8у² + 6у,

      -7у – 53 = -2у + 2,

      -5у = 55,  у = -11.

Відповідь. -11.

2) (3х – 7 – 2х)(3х – 7 + 2х) = 0,

    (х – 7)(5х – 7) = 0,

    х – 7 = 0 або 5х – 7 = 0,

    х = 7       або  х = 1,4.

Відповідь. 7; 1,4.

4*. 1) 36у² + 24у + 4 – 27 =

       = 16y² – 81 + 20у² – 62y – 28,

       24y – 23 = -62y – 109,

       86у = -86, у = -1.

Відповідь. -1.

2) (8y – 1 – 7y)(8y – 1 + 7y) = 0,

    (у – 1)(15у – 1) = 0,

     у – 1 = 0  або 15у – 1 = 0,

     у = 1   або  у = .

Відповідь. 1; .

5*. х² – 4х + 5 = (х² – 4х + 4) + 1 =

   = (х – 2)³ + 1 > 0,  оскільки (х – 2)² ≥ 0.

5*. х² – 14х + 51 = (х² – 14х + 49) + 2 =

  = (х – 7)² + 2 > 0, оскільки (х – 7)² ≥ 0.

6**.

[(а – 1)(а² + а + 1)][(а + 1)(а² – a + 1)]x x(а⁶ + 1)(а¹² + 1)(а²⁴ + 1) =

= [(а³ – 1)(а³ + 1)](а⁶ + 1)х

x(a¹² + l)(a²⁴ + 1) = [(a⁶ – l)(а⁶ + 1)] x

x(a¹² + l)(a²⁴ + l) = [(а¹² – l)(а¹² + l)]x х(а²⁴ + 1) = (а²⁴ – 1)(а²⁴ + 1) = а⁴⁸ – 1

6**. Див. розв'язання варіанта 1 (бо умова відрізняється тільки порядком множників)