Суміжні кути. Властивості суміжних кутів.
Тема. Суміжні кути. Властивості суміжних кутів.
Мета: домогтися свідомого розуміння учнями означення суміжних кутів, засвоєння змісту властивості суміжних кутів, а також сформувати уявлення в учнів про зміст поняття «теорема»; сформувати в учнів уміння розпізнавати на готовому рисунку пари суміжних кутів, будувати кут, суміжний з даним, відтворювати зміст теореми про властивість суміжних кутів та, використовуючи цю властивість, розв'язувати задачі на обчислення суміжних кутів.
Тип уроку: засвоєння знань, вироблення вмінь.
Обладнання: таблиця № 5 «Суміжні кути», набір демонстраційного приладдя.
Хід уроку
І. Організаційний етап
ІІ. Перевірка домашнього завдання
Цей етап уроку можна провести у формі самостійної роботи з наступною перевіркою виконання за готовими розв'язками.
Самостійна робота № 2
|
Варіант 1 |
Варіант 2 |
|
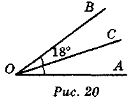
1. Дано: ОС — бісектриса кута АОВ (рис. 20). Знайдіть кут АОВ.
|
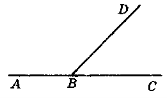
1. Дано: BD — бісектриса кута ABC (рис. 21). Знайдіть кут ABC.
|
|
2. Чи можуть дві прямі, що мають спільну точку, бути паралельними третій прямій? |
2. Чи можуть дві прямі, паралельні третій прямій, мати спільну точку?
|
|
3. Промінь С — бісектриса кута BD, а промінь А — бісектриса кута ВС. Знайдіть кут BD, якщо кут AD |
3. Промінь А — бісектриса кута ВС, а промінь D — бісектриса кута АС. Знайдіть кут АС, якщо кут BD |
III. Мотивація навчальної діяльності учнів
Для створення позитивної мотивації навчальної діяльності учнів можна запропонувати для розв'язання такі завдання.
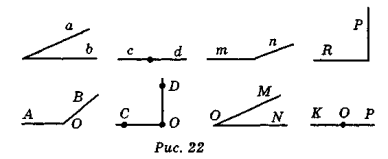
- Кути, зображені на рис. 22, поділіть на групи за їхньою градусною мірою. Які групи ви утворили?
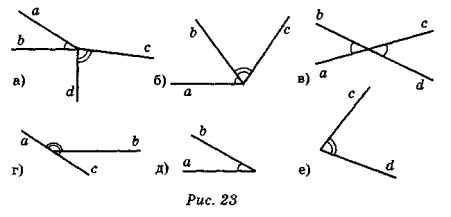
- Опишіть словами, використовуючи назви елементів кутів, особливості взаємного розміщення кутів на рис. 23. Який з випадків а-е зайвий? чому?
IV. Формулювання мети і завдань уроку
Спираючись на спостереження і висновки, отримані на попередньому етапі уроку, вчитель формулює мету уроку (вивчення одного з можливих випадків взаємного розміщення двох кутів) і після узгодження цієї мети з учнями формулює завдання на урок: дати означення нового поняття і навчитися користуватися ним для розпізнавання і зображення, а також дослідити, які властивості має нове поняття і навчитися користуватися ним для розв'язування практичних задач.
V. Актуалізація опорних знань і вмінь учнів
Усні вправи
Знайдіть градусну міру кута АОВ на рис. 24.
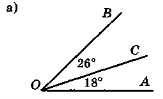
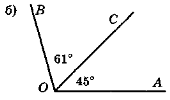


Рис. 24
VI. Засвоєння нових знань
План вивчення нового матеріалу
- Уявлення про спосіб утворення суміжних кутів. Означення суміжних кутів.
- Уявлення про теорему як про один із видів математичних тверджень.
- Теорема про суму суміжних кутів (властивість суміжних кутів).
Методичний коментар
На відміну від традиційного означення, у підручнику Г. П. Бевза міститься конструктивне означення суміжних кутів (тобто кутів, на які розгорнутий кут розбивається своїм внутрішнім променем), а традиційне означення наводиться далі як пояснення способу розпізнавання суміжних кутів.
Оскільки в цій темі учні вперше в шкільному курсі геометрії вивчають теорему, то необхідно пояснити учням зміст цього поняття (для більш свідомого сприйняття можна організувати роботу учнів з тлумачним словником) і на прикладі теореми про суміжні кути розпочати копітку роботу з формування в учнів уявлень про зміст поняття «властивість».
Формулювання та спосіб доведення теореми про суміжні кути, що наведені в підручнику, майже не відрізняються від традиційних, за виключенням того, що в теоремі йдеться про «Суму мір» (а не про суму кутів), а в доведенні розглядається «об'єднання» суміжних кутів (з поняттям об'єднання учні масової школи не знайомі).
Як і на кожному з попередніх уроків геометрії, при вивченні нового матеріалу використовуємо наочність: дивимось табл. № 5 «Суміжні кути».
Таблиця № 5
|
Суміжні кути |
|
|
1. Означення |
|
|
|
Кути ABD і CBD: 1) мають спільну сторону BD;
2) дві інші сторони ВА і ВС — доповняльні промені, тому |
|
2. Властивості |
|
|
|
Якщо |
VII. Первинне усвідомлення нового матеріалу
Методичний коментар
Роботу над закріпленням нових понять необхідно розпочати з виконання вправ на усвідомлення означення суміжних кутів; при виконанні відповідних усних вправ необхідно вимагати від учнів аргументувати свою думку із посиланням на вивчене означення.
Так само при розв'язуванні вправ на усвідомлення означення властивості суміжних кутів необхідно вимагати від учнів спочатку формулювати твердження, що відповідає умові задачі згідно з теоремою, а вже потім виконувати необхідні обчислення.
Усні вправи
- Чи є суміжними кути, зображені на рис. 25?
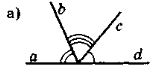
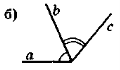
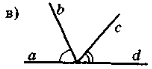

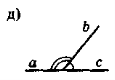

Рис. 25
- Чи є на рис. 26 пари суміжних кутів?
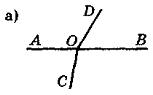

Рис. 26
- Знайдіть градусні міри кутів KLN і LPN на рис. 27.
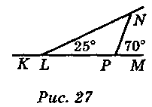
Графічні вправи
Накресліть розгорнутий кут АОВ.
- Проведіть промінь ОС так, щоб кут АОС був тупим. Назвіть утворені суміжні кути.
- Виміряйте транспортиром кут ВОС та обчисліть градусну міру кута АОС, користуючись теоремою про суму суміжних кутів.
- Проведіть промінь OD, що ділить кут АОС на два кути. Скільки пар суміжних кутів утворилося на рисунку?
Письмові вправи
На закріплення поняття властивості суміжних кутів учні виконують вправи № 104, 106, 109 (а).
VIII. Підсумки уроку
Запитання до учнів
- Два кути мають спільну сторону. Чи означає це, що:
а) ці кути мають спільну вершину;
б) ці кути мають дві інші сторони — доповняльні промені;
в) ці кути є суміжними;
г) їх сума дорівнює 180°?
- Градусна міра одного із суміжних кутів дорівнює α. Яка градусна міра другого кута?
IX. Домашнє завдання
- § 4, вивчити означення і теорему 1, усно № 96, 97.
- Письмово: № 105, 108.
Додаткова задача. Бісектриса ділить кут АОВ на два кути, один із яких має градусну міру 50° . Знайдіть градусну міру кута, суміжного з кутом АОВ.


про публікацію авторської розробки
Додати розробку