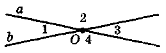
Вертикальні кути. Кут між прямими, що перетинають¬ся

Тема. Вертикальні кути. Кут між прямими, що перетинають­ся

Мета: домогтися засвоєння учнями означення вертикальних кутів, формулювання та схеми доведення теореми про властивість вертикальних кутів; означення кута між пря­мими, що перетинаються; виробити в учнів уміння відтво­рювати вивчені математичні твердження, розпізнавати вертикальні кути на рисунку і будувати вертикальні кути; розв'язувати задачі із застосуванням теореми про суму суміжних кутів і теореми про вертикальні кути.

Тип уроку: засвоєння знань, вироблення вмінь.

Обладнання: набір демонстраційного креслярського приладдя, таб­лиця № 6 «Вертикальні кути».

Хід уроку

І. Організаційний етап    

ІІ. Перевірка домашнього завдання

Учитель збирає зошити учнів для перевірки; учні виконують самостійну роботу.

Самостійна   робота   №  3

Варіант 1

1. З вершини розгорнутого кута АОВ проведено промінь ОС. Назвіть суміжні кути, які при цьому утворилися.
2. Один із суміжних кутів дорівнює 22°. Чому дорівнює другий кут?
3. Один із суміжних кутів на 22° більше за другий. Знай­діть ці кути.

Варіант 2

1. До променя ОР, який є стороною кута МОР, проведено доповняльний промінь ОК. Назвіть пару суміжних кутів, які при цьому утворилися.
2. Один із суміжних кутів дорівнює 132°. Чому дорівнює другий кут?
3. Один із суміжних кутів в три рази більший за інший. Знайдіть ці кути.

III. Формулювання мети і завдань уроку. Мотивація навчальної діяльності учнів

Нагадуємо учням про можливі варіанти взаємного розташу­вання двох кутів зі спільними елементами (див. урок 7), після чого формулюємо мету: сформулювати означення і властивості нового (за взаємним розташуванням) виду кутів, окреслити сферу застосування цих знань.

IV. Актуалізація опорних знань і вмінь учнів

Усні   вправи

1. Знайдіть кут, суміжний з кутом, який становить: а) 30°, б) 90°, в) 120°,    г) α (0 < α < 180°).
2. Дано кут. Один із кутів, суміжних з даним кутом, дорівнює 50°. Чому дорівнює другий кут, суміжний з даним?
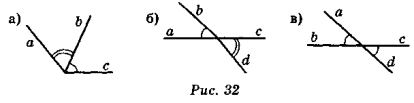
3. Опишіть словами взаємне розміщення кутів, позначених на рис. 32.

V. Засвоєння нових знань

План вивчення нового матеріалу

1. Означення вертикальних кутів.
2. Теорема про вертикальні кути (з доведенням).
3. Застосування означення і властивості вертикальних кутів (кути, що утворилися при перетині двох прямих, кут між двома прямими).

Таблиця № 6

Методичний   коментар

На відміну від означення суміжних кутів, означення верти­кальних кутів, що наводиться у новому підручнику, має такий самий вигляд, який воно мало в традиційному підручнику. Але, щоб зберегти певну логіку викладення навчального матеріалу, перед вивченням означення вертикальних кутів можна за­пропонувати учням накреслити дві прямі, що перетинаються, і розглянути кути, що при цьому утворилися. Після аналізу ситуації формулюються означення і потім властивість верти­кальних кутів.

Незважаючи на те, що поняття кута між прямими не роз­глядається в тексті підручника, воно органічно пов'язане з по­няттями суміжних та вертикальних кутів, тому автор вважає за необхідне вивчити це питання на даному уроці (дати означення, розглянути задачі на знаходження).

VI. Первинне усвідомлення матеріалу

Усні вправи

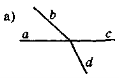
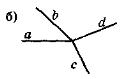
1. Чи є на рис. 33 пари вертикальних кутів? Відповідь обґрунтуйте.

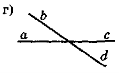
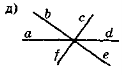
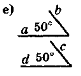
Рис. 33

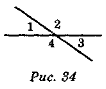
2. Визначте на рис. 34 вид кутів, що утворилися: 1 і 2, 1 і 3, 1 і 4, 2 і 3, 2 і 4, 4 і 3. Порівняйте відповіді. Зробіть висновки.

3. Визначте вид двох кутів, що утворилися при перетині двох прямих, якщо:

а) один із них на  20°   більший за інший;

б) їх сума дорівнює  120°.

Графічні   вправи

Накресліть прямі а і b, що перетинаються в точці О під кутом 80°.

1. Вирізніть однаковим кольором усі пари вертикальних кутів, що утворилися на рисунку. Якими є градусні міри цих кутів?
2. Проведіть через точку О пряму с, що утворює з прямою а прямий кут. Чи буде пряма с утворювати прямий кут з прямою b?

Письмові   вправи

№ 111—113.

Під час розв'язування письмових вправ учні мають викорис­товувати той факт, що при перетині двох прямих утворюються чотири кути, причому будь-які два з них є або суміжними, або вертикальними (тобто або їх сума дорівнює 180°, або вони рівні).

VII. Підсумки уроку    

Запитання  до  учнів

1. Чи можуть дві прямі, перетинаючись, утворити три го­стрі кути; тільки один тупий кут; чотири прямі кути?
2. Чи є правильним твердження: «Два рівні кути зі спіль­ною вершиною є вертикальними»?

VIII. Домашнє завдання    

1. § 5 — вивчити означення та властивість вертикальних кутів.
2. Письмово: № 102,  110,  113.