Текст Урок "Перетворення графіків функції"

Тема: Найпростіші перетворення графіків функцій

Мета: сформувати  розуміння учнями змісту поняття "перетворення графіків функції", формувати практичні уміння виконувати найпростіші перетворення графіків функції за допомогою таких геометричних перетворень, як паралельне перенесення, симетрія, стиснення та розтягування, сформувати первинні уміння "читати графіки функцій" (тобто за відомими графіками) задавати рівняння функцій;

розвивати навички самостійної роботи, дослідницькі навики, формувати вміння аналізувати, порівнювати, узагальнювати вивчені факти;

виховувати працелюбність, самостійність,цілеспрямованість,зацікавленість до вивчення предмета, охайність і точність при виконанні роботи

Тип уроку: урок вивчення нового матеріалу.
Обладнання: таблиця «Найпростіші перетворення графіків функцій», комп’ютер, шаблони графіків , презентація «Найпростіші перетворення графіків»,  презентація «Графіки навколо нас».

 

ХІД УРОКУ

І. Організаційна частина.

Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.

II. Перевірка домашнього завдання

1) Вказати область визначення функції (слайд 1)

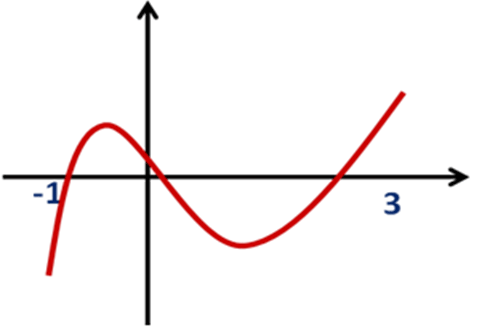
Відповідь:  [ -1; 3]

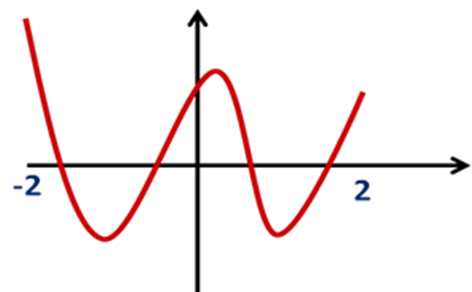
Відповідь:  [ -2; 2]

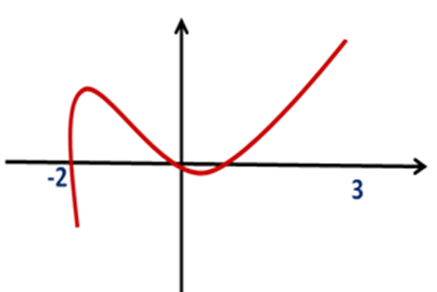
Відповідь:  [ -2; 3]

2) Вказати область значення функції (слайд 2)

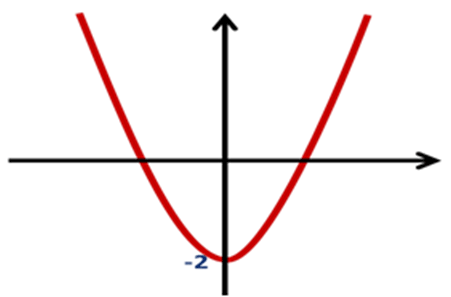
Відповідь: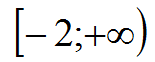 

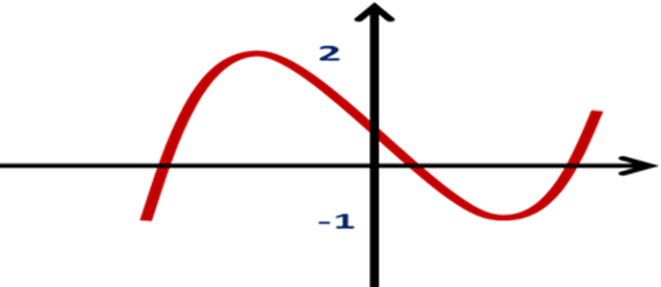
Відповідь: [ -1; 2]

3)  Вказати нулі функції: (слайд 3)

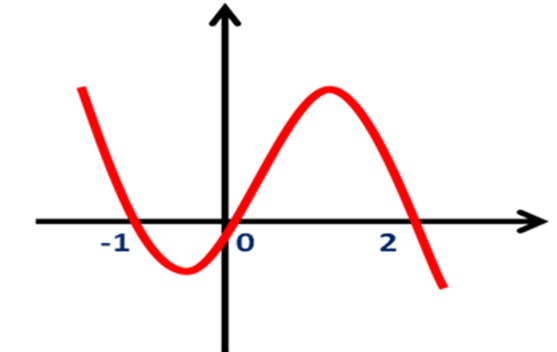
Відповідь: х= -1; х=0; х=2

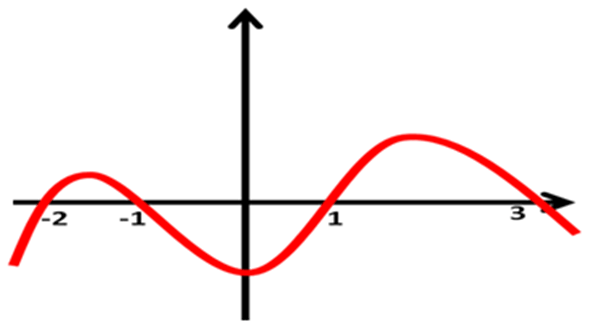
Відповідь: х=-2; х= -1; х=1; х=3

4) Визначити: зростаюча чи спадна функція (слайд 4)

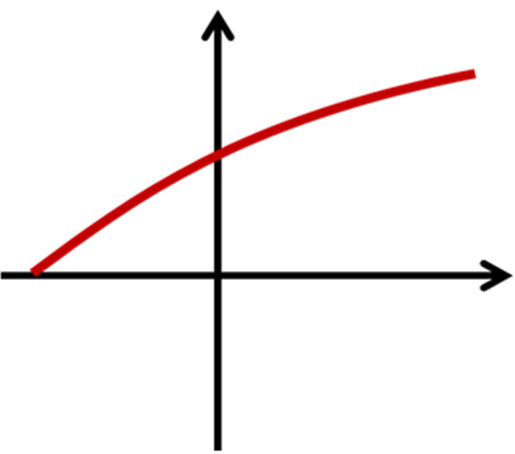
Відповідь: зростаюча

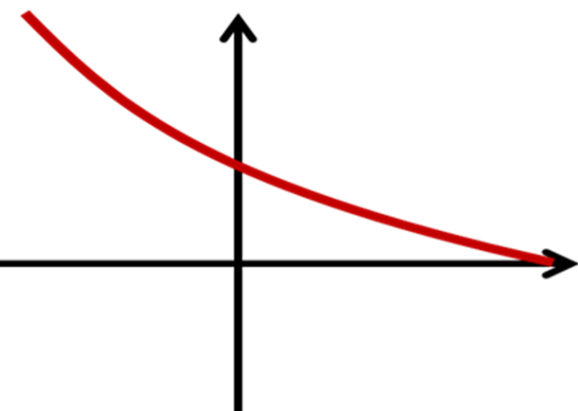
Відповідь: спадна 

Математичний диктант

1. Залежність, при якій кожному значенню аргументу відповідає одне єдине значення у, називається …

2.Назвіть способи завдання функції.

3. Усі значення, які набуває незалежна змінна, називаються областю …

4. Усі значення, які набуває залежна змінна, називаються областю …

5. Для побудови прямої, яка є графіком лінійної функції, потрібно … точки.  

 

ІІІ. Актуалізація опорних знань.

1.Знайдіть область визначення функцій:

a)      

б) Зробіть висновок.

2. Точки А(1;1), В(2;4), С(3;9) належать графіку функції Знайдіть ординати точок із тими ж абсцисами, що й точки А, В, С, які належать графіку функції   Зробіть висновок.

 

 

ІV.Формулювання теми і задач уроку. Мотивація навчання.

План вивчення теми

1. Побудова графіка функції якщо відомий графік функції

2. 1. Побудова графіка функції якщо відомий графік функції

1. Побудова графіка функції якщо відомий графік функції

1. Побудова графіка функції якщо відомий графік функції

 

«Коли починаєш справу, спитай себе: «Що я маю зробити?»

Після закінчення: «Що я зробив?»

                                                                          Піфагор

       Запас функцій, графіки яких ви вміли будувати, був невеликий. Вико-ристовуючи відомості про перетворення графіків функцій, цей список можна суттєво розширити.

А навіщо?

Презентація «Де ми зустрічаємось з графіками»

Сьогодні ми продовжимо вчитися будувати графіки більш складних функцій за допомогою перетворень.

V.Формування знань.

Для вивчення нових перетворень графіків ми розіб’ємося на 2 групи. Завдання для вивчення та презентації нової теми отримаєте з «квітки жасміна», як назвали петлю Декарта.

У сучасному вигляді її представив Гюйгенс.

 

 

 

І група «Абсциса»

ІІ група «Ордината»

(На дошці квітка-петля Декарта з видами перетворень.)

Відривають лепестки – завдання та готують за підручником Ю.І. Мальований

п.4.2. «Перетворення графіків»

Групи працюють за планом з матеріалами підручника:

прочитати відповідне пояснення у підручнику, розібрати його, записати правило, вивчити, зобразити графік перетворення функції  у=х² на А-4.

Презентація-пояснення відповідного перетворення кожної групи на слайдах презентації.

VІ.Формування вмінь. Закріплення матеріалу

Розв’язання вправ за підручником № 231а)б), № 232 а) б), № 233а) г).

Побудуйте в одній координатній площині графіки функцій:

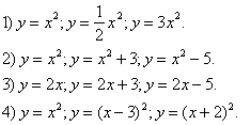
VІІ. Первинна перевірка знань

Розкажіть, за допомогою яких перетворень можна дістати із графіка функції  у=х² графік функції:

1) у=х²-1;

2) у=х²+1;

3) у=;

4) у=;

5) у=

Робота в групах

 

 

 

 

 

 

 

 

 

 

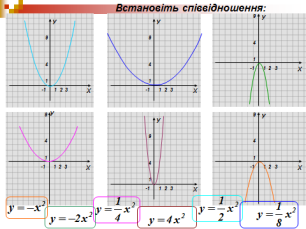
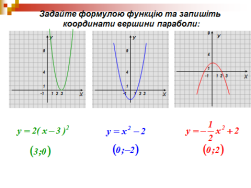
VIII.Рефлексія досягнень.

Підводяться підсумки уроку. Учні в групах виставляють оцінки одне одному. Вчитель оцінює усю групу в цілому. При виході з класу прикріплюють смайлик настрою та знань на піраміду Знань.

X. Підсумок уроку. Домашнэ завдання.

Вивчити п.4.2( правила)

Розв'язати вправи № 248, № 225.