Урок"Прогресія навколо нас"
Тема уроку: Прогресії навколо нас.
Розв'язування задач прикладного змісту.
Мета. Узагальнити знання учнів про прогресії, закріпити навички обчислення суми, показати практичне застосування теми на прикладах задач із життя та історичних задач; розвивати вміння учнів створювати математичні моделі до розв'язування задач; виховувати інтерес до знань; сприяти творчому розвитку учнів.
Тип уроку: урок-семынар. Урок систематизації і корекції знань і вмінь
Обладнання. Таблиці, дидактичний матеріал, портрети видатних математиків.
Девіз: "...Математика безмежно різноманітна, як світ, і присутня, міститься в усьому." (М.П. Єругін).
Хід уроку
І. Постановка мети і завдань уроку
На сьогоднішньому уроці ми узагальнимо свої знання про прогресії, покажемо практичне застосування теми на прикладах задач із життя та історичних задач.
ІІ. Актуалізація опорних знань учнів
Розумова розминка.(учні розв’язують кросворд)
По вертикалі: 1.Послідовність, у якій кожний наступний член менший за попередній.
2.Послідовність чисел, у якій кожний член. починаючи з другого, утворюється множенням попереднього на стале число.
3. Нескінченна або скінченна сукупність чисел.
4.Слово „прогресія” у перекладі з латинської означає „рух вперед” або...
5. Знаменник геометричної прогресії -3; -9; -27; -81;... дорівнює...
6. Стале число, множенням на яке утворюється кожний наступний член геометричної прогресії.
7.Різниця арифметичної прогресії 15,21, 27,...33,...
8. Число, додаванням якого утворюється кожне наступне число у арифметичній прогресії.
9. Термін „прогресія” вперше зустрічається у римського автора Боеція у... столітті. 10. По горизонталі ви прочитаєте слово...
Відповіді. 1. Спадна. 2. Геометрична. 3.Послідовність. 4.Прогрес. 5. Три. 6. Знаменник. 7.Шість. 8.Різниця. 9.П'яте.
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
1 |
|
|
|
5 |
|
|
8 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
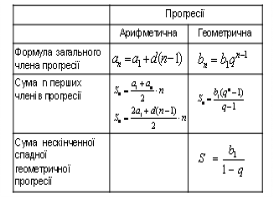
Перевір себе.
Учням кожного ряду видається конверт. В цьому конверті картки, на яких написані частина формул. Завдання кожної групи: зібрати правильно ці формули, їх всього 8 формул. В конверті можуть бути і зайві картки.
Перевірка виконується після появи правильних відповідей на слайді..
|
|
a1 |
d |
an |
n |
sn |
|
1 |
1 |
|
28 |
10 |
|
|
2 |
10 |
-2 |
|
8 |
|
|
3 |
|
|
15 |
6 |
60 |
|
4 |
3 |
|
-18 |
|
-60 |
|
5 |
1 |
3 |
28 |
|
|

|
|
b1 |
q |
bn |
n |
sn |
|
1 |
1 |
3 |
|
|
|
|
2 |
64 |
1/2 |
2 |
|
|
|
3 |
|
2 |
640 |
8 |
|
|
4 |
6 |
|
96 |
5 |
-60 |
|
5 |
2 |
|
32 |
5 |
|
Перший варіант заповнює таблицю „ Арифметична прогресія”, другий варіант заповнює таблицю „Геометрична прогресія”. Одержаний результат кожний учень заносить в таблицю.
Цікаві факти.
Хімія. При підвищенні температури по арифметичній прогресії швидкість хімічної реакції росте по геометричній прогресії.
Геометрія. Вписані один в одного правильні трикутники утворюють геометричну прогресію.
Біологія. Мікроорганізми розмножаються способом поділу пополам, тому при сприятливих умовах через однаковий проміжок часу їх число подвоюється , і утворюють геометричну прогресію.
Фізика. У фізичних процесах також зустрічається ця закономірність. Нейтрон вдаряючи по ядру урану , розкладає його на дві частини. Утворюється два нейтрони. Потім два нейтрон вдаряючи по ядру урану , розкладає його на чотири частини, і т. д.- це геометрична прогресія.
Економіка. Вклади в банк щорічно збільшуються на однаковий процент.
-Сьогодні у нас в класі відбудеться засідання Ради Мудреців.
(Мудреці сидять за окремим столом.) Чи впізнаєте ви їх?
(За столом сидять Архімед. Гаус, Магницький).
Гаус: О! Я – Карл Гаус. Знайшов миттєво суму всіх натуральних чисел від 1 до 100, коли був учнем початкової школи.
Архімед. Хто формулу суми квадратів знайшов? І правильною дорогою до прогресу привів. Математик і фізик. Я Архімед. Про життя моє є багато легенд.
Магницький. Панове! Дозвольте познайомитись. Я – Леонтій Пилипович
Магницький створив перший підручний “Арифметика”.
Вчитель: Скажіть, діти, чому ці вчені математики раптом зібрались за
одним столом. Яке питання математики їх об’єднує?
(діти висловлюють свої думки )
Підсумовуванням арифметичних і геометричних прогресій та складанням відповідних задач займалися багато любителів математики протягом багатьох століть. У довньоруському юридичному збірнику "Руська правда" містяться відомості про приплід від худоби і бджіл за певний відомий проміжок часу, про кількість зерна, зібраного і визначеної ділянки землі та ін. Ці задачі, очевидно, не мали господарського чи юридичного значення, а, як і в інших країнах, були результатом розвиткук інтересу до математики иа математичного змісту даних задач.
Проте вперше задачі на прогресії виниклі зі спостережень над явищами природи і з досліджень суспільно-економічних явищ, до яких можна застосувати закон прогресії.Так, у вавилонських текстах розповідається про те, що збільшення освітленої частини місячного диска протягом перших п'яти днів відбувається за законом геометричної прогресії зі знаменником 2, у наступні 10 днів - за законом арифметичної погресії з різницею 16. Широкий інтерес вавилонян до астрономії робить зрозумілим виникнення цієї задачі.
«Приклади в навчанні корисніші за правила.»
Ісаак Ньютон
Клас бав поділений на групи і працював над проектом “Прогресія навколо нас”
Історична довідка
"Прогресія", "прогрес", "прогресивний" - слова одного кореня. Прогресія - це послідовність, побудована за таким законом, який дає змогу продовжувати її необмежено, тобто рухатися вперед.
Прогресія - явище без перебільшення, унікальне. Історія виникнення прогресії сягає глибини віків.
Перші задачі на прогресії пов'язані із запитами господарського життя і суспільної практики (розподіл спадщини, одержання винагороди), із спостережень над явищами природи, з досліджень суспільно-економічних явищ. Так, у вавилонських текстах розповідається про те, що збільшення освітленої частини місячного диска протягом перших п'яти днів відбувається за законом геометричної прогресії зі знаменником 2, у наступні 10 днів - за законом арифметичної прогресії з різницею 16. Широкий інтерес вавілонян до астрономії робить зрозумілим виникнення цієї задачі.
Зміст ряду історичних задач на прогресії, відбиває той подив, який викликало в тих, хто розв'язував ці задачі.
Із виступів знавців історії
- Розв’язання задач (інсценізація задачі ”Винагорода”)
Умова задачі
Полководець Теренцій за наказом імператора переміг у черговому поході і з трофеями повернувся до Риму. Прибувши до столиці, він прийшов на прийом до імператора.
- Багато перемог здобув я, щоб звеличити твою міць, імператоре. Я не боявся смерті. Але я втомився. Настав час відпочити.
- Чого ж ти хочеш від мене? – запитав імператор.
- За довгі роки військового життя я не встиг створити собі грошового статку. Нехай щедрість твоя допоможе мені дожити мирно і в достатку.
Імператор не відрізнявся великою щедрістю. Він любив нагромаджувати гроші для себе і скупо витрачав їх на інших. Прохання полководця змусило його замислитися.
- Яку ж суму ти хотів би для себе, Теренцію?
- Мільйон динарів, імператоре.
Імператор пообіцяв дати відповідь завтра. Наступного дня в призначену годину Полководець прийшов до палацу.
- Вислухайте мене, воїне, - сказав імператор, - у моїй скарбниці лежить 5 мільйонів брасів ( 1 брас = ![]() динарія). Ти ввійдеш до скарбниці, візьмеш одну монету в руки, повернешся сюди і покладеш її до моїх ніг. Другого дня візьмеш монету, що дорівнює 2 брасам. Третього дня принесеш монету в 4 браси, четвертого у 6 брасів і т.д., щоразу подвоюючи вартість монети. Я накажу щодня виготовляти для тебе монети потрібної цінності. І поки вистачить у тебе сили піднімати монети, ти будеш виносить їх. Ніхто не має права тобі допомагати, ти повинен користуватись лише власними силами. І коли помітиш, що не можеш більше підняти монету, зупинишся, домовленість наша закінчена, а всі монети, що ти виніс, залишаться тобі і будуть твоєю винагородою.
динарія). Ти ввійдеш до скарбниці, візьмеш одну монету в руки, повернешся сюди і покладеш її до моїх ніг. Другого дня візьмеш монету, що дорівнює 2 брасам. Третього дня принесеш монету в 4 браси, четвертого у 6 брасів і т.д., щоразу подвоюючи вартість монети. Я накажу щодня виготовляти для тебе монети потрібної цінності. І поки вистачить у тебе сили піднімати монети, ти будеш виносить їх. Ніхто не має права тобі допомагати, ти повинен користуватись лише власними силами. І коли помітиш, що не можеш більше підняти монету, зупинишся, домовленість наша закінчена, а всі монети, що ти виніс, залишаться тобі і будуть твоєю винагородою.
- Я задоволений твоєю милістю, імператоре, - радісно відповів Теренцій, уявляючи величезну кількість монет, і одна більше від іншої.
Почалися щоденні відвідування Терентієм скарбниці. Першого дня він виніс 1 брас монету, 21 мм діаметром і вагою 5 г. Легкими були і 2-й, 4-й, і 6-й переходи. Сьома монета важила вже 320г і була 84мм у діаметрі, восьма – 640г і діаметром 10,5 см, дев’ята – 1кг 250 г і 13 см у діаметрі.
Імператор не приховував свого тріумфу. Він бачив, що зроблено 12 переходів, а винесено лише 2000 мідних монеток. На 14 день полководець виніс зі скарбниці монети вагою 41 кг і 42 см у діаметрі.
- Чи не втомився ти, мій хоробрий Теренцій? – запитав його імператор, стримуючи посмішку.
- Ні, імператоре, - похмуро відповів полководець.
Настав 15-й день. Теренцій ніс монету вагою 82 кг і 53 см у діаметрі. На 16-й день полководець хитався під ношею, що лежала в нього на спині вагою 164 кг, 67 см у діаметрі. Коли Теренцій з’явився у приймальні імператора на 17-й день, його зустрічали дружнім сміхом, він не міг уже нести свою ношу в руках, а котив її перед собою. Монета важила 328 кг.
- Не можу більше, вистачить.
Чи дістав Теренцій мільйон динарів? Ні. (S17 = 131072 динарів)
Задача 2: Легенда про винахід шахів.
Шахову гру винайшли в Індії. Ознайомившись з нею, індійський цар Шерам, захоплений дотепністю і різноманітністю можливих в ній ситуацій, покликав до себе її винахідника, ученого Сету, і сказав йому:
"Я хочу гідно нагородити тебе, Сета за прекрасну гру, яку ти придумав. Я досить багатий, щоб виконати будь-яке твоє бажання."
"Володарю, - відповів Сета, - накажи видати мені за першу клітинку шахівниці одну пшеничну зернину, за другу - 2 зернини, за третю - 4, і так за кожну клітинку вдвічі більше, ніж за попередню".
"Ти одержиш свої зерна. Але знай, що твоє прохання не варте моєї щедрості. Іди. Слуги мої винесуть тобі твій мішок із пшеницею".
На другий день придворні математики з'явились до царя.
"Ми ретельно обчислили, - говорили вони йому, - усю кількість зерна, що бажає одержати Сета. Число таке велике, що зерен не вистачить ні в яких коморах, навіть цілого царства. Не знайдеться такої кількості зерен і на всьому просторі Землі. І якщо ти обов'язково хочеш видати нагороду, то накажи перетворити всі царства в поля, висушити всі річки та озера, розчинити криги та сніги. Увесь цей простір засій пшеницею й усе, що виросте на ньому за 5 років, накажи віддати Сеті. Тоді він одержить свою винагороду."
Зі здивуванням слухав цар Ширам слова вчених. "Напишіть же мені це дивовижне число"- сказав він.
Розв'язання:
Кількість зернин, про які йдеться в задачі, є сумою 64 членів геометричної прогресії, у якої ![]() ,
,
![]() =18446744073709551615, що приблизно становить 13,8 млрд. 40-тонних вагонів.
=18446744073709551615, що приблизно становить 13,8 млрд. 40-тонних вагонів.
Якщо таку кількість зернин рівномірно розсипати по всій земній поверхні, то утвориться шар пшениці товщиною 9-мм.
Задача 3. Купівля коня.
(Із арифметики Магницького.)
Продавець продав коня за 156 крб. Але покупець, придбавши коня, передумав і повернув його господарю, кажучи:"Нема мені користі купувати за таку ціну коня, який таких грошей не вартий". Тоді продавець запропонував інші умови: "Якщо ціна за коня дуже висока, то купи лише цвяхи для його підков. а коня одержиш безплатно на додачу. Цвяхів у
кожній підкові 6. За перший дай мені всього 1/4 к., за другий – 1/2 к., за третій - 1к. і т. д..." Покупець, спокусившись низькою ціною та бажаючи безплатно придбати коня, прийняв умови, думаючи, що за цвяхи доведеться заплатити не більше 10 крб. На скільки покупець проторгувався?
Розв'язання:
Маємо геометричну прогресію у якої ![]() 1/4,
1/4, ![]() .
.![]() .
.
За таких умов можна дати й коня на додачу.
Задача 4. Мешканець маленького містечка був відомий своєю скнарістю. Коли у нього були справи в повітовому місті, розташованому в 25 км від цього містечка, він звичайно шукав сусідів, які б підвезли його. Одного разу скнара крутився на площі, шукаючи того, хто підвіз би його за спасибі додому. Але цього разу нікого не було і він змушений був шукати платного візника. Скнара обійшов їх усіх, торгуючись з ними і порівнюючи ціни. Один просив 250 руб., другий - 200 руб., третій -150. Усі ці ціни здалися йому занадто високими. Нарешті він помітив візника з убогим візком і жалюгідною шкапою. Коли скнара запитав його скільки він візьме за дорогу, той подивився на землю, почухав потилицю і відповів: "за 1-й кілометр заплати мені 1 коп., за другий - 2 коп, за 3-ій - 4, за 4-ий - 8 і так до кінця шляху."
"От дурний - подумав скнара, ледве стримуючи сміх, - лічить на копійки." Поспіхом він заліз у візок і гукнув:"Згідний! Поїхали!"
Скільки грошей він повинен заплатити за дорогу?
Розв'язання:
1; 2; 4; 8; 16;... - геометрична прогресія.
![]() .
.
![]() (коп.)=335544 руб. 31 коп.
(коп.)=335544 руб. 31 коп.
Задача 5. У газеті, що була виданау1914р., описувалася справа, яка відбулася у місті Новочеркаську, про продаж отари, що має 20 овець, за такими умовами: за першу вівцю слід заплатити 1 к., за другу - 2 к., за третю - 4 к. і т. д. У яку суму обійдеться вся отара?
Розв'язання:
1; 2; 4; 8;... - геометрична прогресія,
![]() .
.
![]() =1084575=11000 (крб.).
=1084575=11000 (крб.).
Із виступів майбутніх архітекторів, будівельників.
Усі ми знаємо, що в архітектурі, будівельній справі широко використовуються колони. Виявляється, вони мають форму не циліндра, як здається на перший погляд, а зрізаного конуса.
Будівельники знають, що сила тиску в горизонтальних шарах будівельної колони зростає у напрямку до нижньої основи. Для збереження рівномірності напруги від тиску вздовж усієї довжини колони потрібно збільшувати площі її поперечних перерізів. Встановлено, що площі поперечних перерізів, рівновіддалених один від одного, становлять геометричну прогресію.
Враховуючи таку закономірність, колони будують не тільки красивими, фігура й міцними та надійними.
Оскільки площі поперечних перерізів колони збільшуються у напрямку до її основи, то колона не може мати форму циліндра.
Задача 6. Знайти площу нижньої основи бетонної колони висотою 3 м, коли відомо, що площа верхньої основи колони 16 дм2, а площа перерізу, розміщеного на 2 м нижче, дорівнює 16,29 дм2.
Розв'язання:
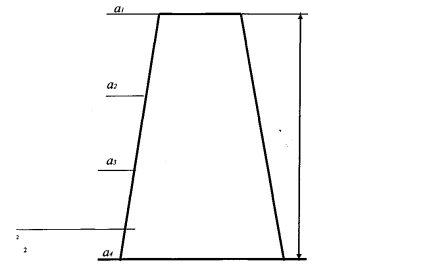
Розглянемо осьовий переріз колони.
За умовою задачі матимемо: ![]() ;
;![]()
![]() (дм2).
(дм2).
Задача 7. Побудова теплиці.
Потрібно виготовити вертикальні стержні для теплиці з дроту так, щоб найменший мав довжину 5 м, а кожний наступний був на 2 м довший (до 7 стержня). Обчисліть довжину дроту, необхідну для виготовлення стержнів. 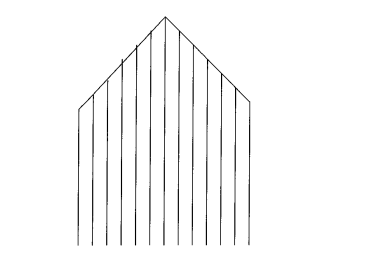
Розв'язання:
Маємо арифметичну прогресію (![]() ), де
), де ![]() .
.
![]() (м)
(м)
Із виступів знавців фізики
Розглянемо ситуацію, пов'язану з використанням геометричної прогресії у фізиці.
Задача 8. Після кожного руху поршня розріджувального насоса з посудини видаляється 20% повітря, що міститься в ній. Визначити тиск повітря всередині посудини після шести рухів поршня, якщо початковий тиск був 750 мм рт. ст.
Розв'язання:
Оскільки після кожного руху поршня з посудини видаляється 20% повітря, що міститься в ній, то залишається в ній 80% повітря. Щоб визначити тиск повітря в посудині після чергового руху поршня, треба тиск повітря після попереднього руху поршня помножити на 0,8: 750; 750*0,8; 750*0,8*0,8; 750*0,8*0,83; ...; 750*0,86. Маємо геометричну прогресію, перший член якої 750, а знаменник 0,8. Число, що визначає тиск повітря всередині посудини після шести рухів поршня, є сьомим членом цієї прогресії і дорівнює 750*0,86.
Задача 9. При вільному падінні тіло проходить за першу секунду 4,9 м, а за кожну наступну на 9,8 м більше. Знайдіть глибину шахти, якщо камінець досяг її дна через 8 с після початку падіння.
Розв'язання:
Маємо арифметичну прогресію, у якої ![]() .
.
![]() .
.
Із виступів майбутніх фінансистів
Задача 10. Уявіть, що вам деяка фірма пропонує свої послуги. Щодня ви можете брати у фірми по 100 грн. Але за перший день ви зобов'язані заплатити фірмі 1к, за другий - 2к, за третій - 4к. і т. д. Чи укладете ви з цією фірмою договір не менш ніж на 20 днів за таких умов?
Розв'язання:
Від фірми отримуємо - 2000 грн, а повинні будемо заплатити за це суму, що дорівнює 8го для геометричної прогресії, де ![]() . Тобто:
. Тобто:
![]() 1048575(коп.)=10485грн. 75к
1048575(коп.)=10485грн. 75к
Задача 11. Ви хочете узяти у банку кредит на 10000 гривень. Умови кредитування: за перший день ви маєте сплатити фірмі 1 копійку, за другий – 3 копійки, за третій – 9 копійок і т.д. Чи уклали б ви з цим банком договір не менше ніж на 30 днів?
Вчитель робить зауваження, що в сучасних ринкових умовах учні повинні бути компетентними у фінансових питаннях, і тому освіченість особистості, як ніколи, на першому місці.
Задача 12. Представники двох рекламних агентств хочуть запропонувати свої послуги. Фірма "Прогрес" на професійному рівні виготовить різноманітні рекламні проспекти вашого міні маркету. Умови оплати такі: за першу партію 100 у.о., а кожна наступна на 4% дешевша за попередню. Представник фірми « Омега» пропонує вам послуги своєї фірми. Умови оплати: перша партія коштує 100 у.о., а кожна наступна має знижку 10%. Порахуємо чия пропозиція вигідніша.
Розв'язання.
Фірма «Прогрес»: те, що кожна наступна партія на 4% дешевше попередньої, говорить нам про те, що маємо справу з геометричною прогресією а1 = 100, d = - 4 .
Фірма « Омена»: знижка 10% означає, що маємо справу з геометричною прогресією в1 = 100,
q =0,9 ( 100% - 10 % = 90 % = 0,9 )
Якщо треба розмістити замовлення на 3 партії, то необхідно знайти S3. Зробимо обчислення:
Фірма «Прогрес»
S3 = в1 * (q*n – 1)/ (q – 1)
S3 = 100 * (0, 93 – 1)/ (0, 9 – 1) = 271 у.о.
Фірма « Омега»
S3 = (2a1 + d*2)/2*n
S3 = (2* 100 – 4*2)/2*3 = 288 у.о.
Висновок: вигідніше розмістити замовлення, використавши послуги фірми « Прогрес».
Задача13 . Уявімо, що на початку нашої ери Єва народила дві доньки, кожна з них до 30 років народила теж дві доньки і т.д. Чи можливо це? Скільки б за таких умов нащадків Єви жило б у наш час?
Розв'язання. Це близько 7∙1019, що значно перевищує кількість людей на планеті. Тому це не можливо.
Задача 14. брудних рук. Слайд 30. Бактерія, потрапивши в організм людини, до кінця 20-ї хвилини ділиться на 2, кожна з них через 20 хв ще на дві і т.д. Скільки бактерій стане в організмі людини через добу?
Розв’язання. Слайд 31.
1доба=24год.; 24год.=1440хв.; 1440:20=72
За умовою задачі отримаємо геометричну прогресію: 1;2;4;8;…;
b1=1, q=2
Sn=((b1(qn-1)):q-1)=((1*(272 -1)):1)= 272 - 1≈ 272(бактерії)
Відповідь: в організмі за добу буде 272 бактерій.
Задача про шкідливість паління 15. Кожен курець викурює в день у середньому 8 цигарок. Після викурювання першої цигарки в легенях осідає 0,0002г нікотину й тютюнового дьогтю. З кожною наступною цигаркою ця кількість збільшується на 0,000001г. Яка кількість речовин осідає в легенях за рік?
Розв'язання. Слайд 33.Отримаємо арифметичну прогресію, де а1=0,0002, d=0,000001. Знаходимо S365
2a1 + d(n-1)
S365= ‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑ n
2
2*0,002 + 0,000001*364
S365=‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑ 365
2
S365= 0,79643г якщо курець викурюватиме 1 цигарку в день.
Якщо ж він буде викурювати по 8 цигарок то кількість речовин, що осідає у його легенях збільшиться в 8 разів, тобто 6,37144г.
Кожні шість секунд тютюн забирає одне життя. Щорічно куріння стає причиною смерті 5,4 мільйонів чоловік. До 2030 р. кількість смертей внаслідок куріння збільшиться до 10млн чоловік за рік. Не куріть!
Із виступів майбутніх літераторів.
Задача 15. Арифметичну прогресію можна зустріти в літературі. Згадаємо віршові розміри: ямб, хорей, дактиль, амфібрахій, і анапест. Відмінність між ними в кількості стоп і в різних розташуваннях наголошених складів вірша.
Як лисиця та вовк рибу дiлили. Вкрали лисиця з вовком риби багатенько, та й давай дiлитись.
— Я не дуже тямущий у математицi, — каже вовк, — дiли ти, але так, щоб порiвну.
— Ось тобi одна рибка, а менi двi, — каже лисичка.
— Чи не замало?! — стривожився вовк.
— Та нi, — каже лисичка, — слухай далi. Ось тобi три рибки...
— Так можна, — заспокоївся вовк.
— Менi 4, а тобi 5, менi 6, а тобi 7...
Так дiлила лисичка рибку, щоразу збiльшуючи на одну рибину. Наостанку вона кинула собi
20 рибин i на цьому риба закiнчилась. Вовк подумав, що лисиця чесно подiлила. А ти як
гадаєш, у кого бiльше риби i на
скiльки?
IІІ. Підсумок уроку.
Що можна сказати про математику і зокрема - про послідовності? Чи зустрічаються вони в житті? Чи пов'язані вони з життям? Як і де саме?
Інтерактивна вправа"Моя теза". Запронувати учням класу записати одним реченням на аркуші паперу головну ідею вивченого. Кожен за сорок п'ять секунд спробує переконати сусіда, що саме його теза важливіша за іншу. А далі пара на таких самих умовах переконує іншу пару про важливість уже їхньої спільної тези.
Об'єднана четвірка переконує іншу, і так доти, доки учні одного ряду не виберуть свого речника, який від їхнього імені одним реченням на окремому аркуші паперу напише підсумок вивченого. Кожен чіпляє свій аркуш на дошку. Кількість тематично схожих висновків згодом визначатиме колективну думку про головну ідею уроку.
Рефлексія.
- На сьогоднішньому уроці ми дізналися....
- Я б не хотів бути на місці....
- На сьогоднішньому уроці найважливішим відкриттям для мене було....
- Я б запитав одного з Мудреців про....
- На початку уроку я поставив перед собою мету. Ось як я її досяг....
- Сьогодні на уроці мені сподобалось....
- Сьогодні на уроці мені було важко....
Заключне слово вчителя:
Урок на сьогодні завершено,
Але кожен повинен знати:
Пізнання, наполегливість, праця
До прогресу в життя приведуть!
ІV. Домашеє завдання. Скласти магічний квадрат.


про публікацію авторської розробки
Додати розробку
