Тема: Функції та їх графіки. Властивості функції.

Кузбит Іван Михайлович,

вчитель математики та інформатики Самбірської гімназії

 

Тема уроку.   Функції та їх графіки. Властивості функції. (5-Б клас)

Мета уроку:   систематизувати знання учнів з теми; закріпити вміння знаходити функції за заданими  формулами; поглибити знання знаходження відповідності даних функцій із формулами; побудова графіків квадратичної функції та вивчення властивостей функції; створити  умови для формування умінь аналізувати та порівнювати; розвивати логічне мислення; виховувати тактовність у спілкуванні.

Тип уроку:     підсумковий урок.

Обладнання:

ноутбук;мультимедійний проектор, мультимедійна дошка;

додаток до уроку: (Презентація.) – в електронному вигляді; програмне     забезпечення для мультимедійної дошки, завдання для уроку виконане в програмі NoteBook, програма для побудови графіків функцій Advanced Grapher, на кожній парті збірники завдань та матеріали із завданнями, картка для самооцінювання знань учнів.

 

Хід уроку

 

Презентація

І. Організаційний момент.

Добрий день діти! Я радий сьогодні вас бачити і дуже надіюся на спільну працю. Сьогодні ми проведемо підсумковий урок по вивчених темах, де згадаємо матеріал не тільки 9 класу, але і попередніх років. Ми будемо з вами працювати як колективно так і в парах, самостійно набувати та закріплювати знання в ігрових формах.

Початок показу слайдів. Повідомлення теми уроку.(Презентація. Слайд  1)

 

 

 

 

 

 

 

 

 

 

 

 

 

Які слова ми знаємо, що пов’язані з темою? (абсциса, ордината, область визначення, координата точки, область значень функції, нулі функції, властивість та інші.)

Тепер давайте сформулюємо мету нашого уроку. (Презентація. Слайд 2)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ІІ. Актуалізація знань учнів.

Дати відповіді на запитання:

Дайте означення функції.

Назвати способи якими задається функція?

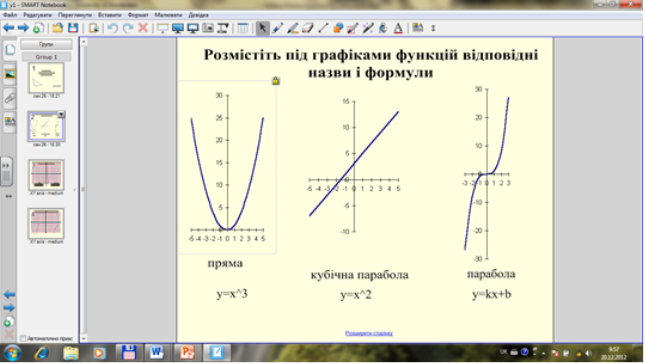
Які з даних графіків є графіками функцій?   (Презентація. Слайд 3)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Що називають аргументом функції? значенням функції? областю визначення функції?

Назвати формули, що задають:

• лінійну функцію (Презентація. Слайд  4);
• функцію прямої пропорційності (Презентація. Слайд 5);
• функцію оберненої пропорційності (Презентація. Слайд 6).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Що називають графіком функції?

А тепер за допомогою графіка функції вказати область значень, нулі, проміжки зростання та спадання функції. (Презентація. Слайд 7)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

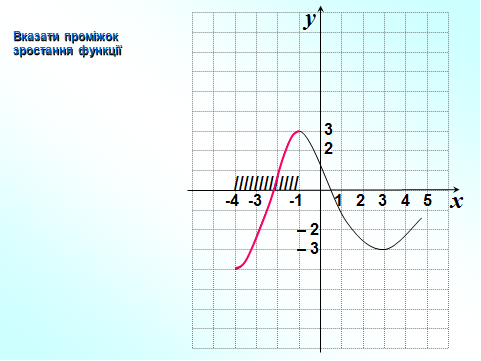
Робота в парах.

Аналогічне завдання тепер виконаємо у зошитах самостійно та перевіримо один в одного у товариша за партою. (Презентація. Слайд 8)

 

ІІІ.   Розв’язування вправ

Ми з вами повторили матеріал, а тепер можемо перейти до математичного диктанту.

 І   Математичний диктант. (Презентація. Слайд 11)

 

1. Назвати абсцису точки А (4 ; 7)
2. Функцію задано формулою у = 4х – 5. Знайти у(-2)
3. Записати область визначення функції у =
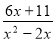
4. Знайти нулі функції у = 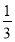х + 12
5. Функцію задано формулою у = 5х + 15. Знайти х , якщо у(х) = 10
6. Знайти область визначення функції у =

А тепер перевіримо виконання математичного диктанту. (Презентація. Слайд 12)

 

 ІІ   Гра “Хто швидше“ (гра на дві команди)

   1 команда     2 команда

1.  f(х) = х² – х + 1. Знайти:

a) f(0) + f(– 9) – f(2) + f(8);  б) f(10) – f(1) + f(3) + f(– 7).

 

 2.  Знайти область визначення функції:

 а) у = 3х – 2;    б) у = 5х + 1;

 в) у = ;     г) у = ;

 д) у = ;   е) у = ;

 є) у = ;    ж) у = .

 

 3. Знайти нулі функції:

 а) у = х² – 4х – 5;    б) у = х² – х – 6.

 

  

 IV  Побудова графіка функції у = (х+m)² + n .

 а) Учням пропонується нагадати  алгоритм побудови графіка функції 

у = (х+m)² + n. (Презентація. Слайд 13)

 

 

 

б) А тепер розглянемо алгоритм побудови графіка функції у = (х+3)² + 4. (Презентація. Слайд 14)

Ми знаємо, що графік функції у = х² можна паралельно переносити вгору, вниз, вправо та вліво. І зараз ми з вами знайдемо залежність між формулами та записами. (Презентація. Слайд 9)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

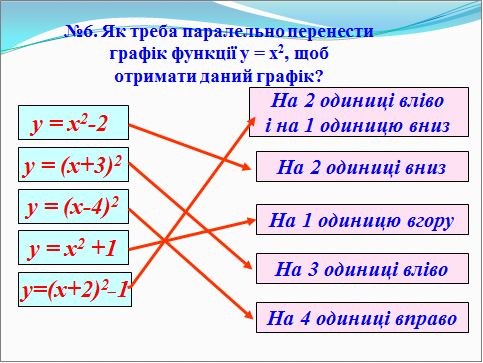
в) Робота учнів самостійно у зошитах:

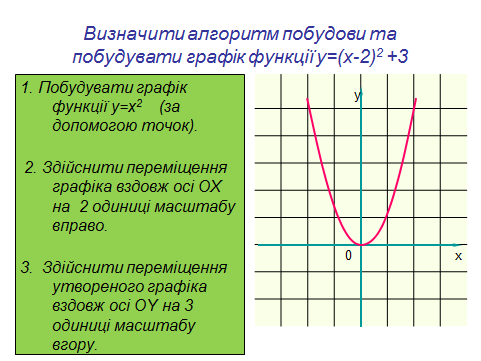
Побудувати графік функції  у = (х – 2)² + 3. (Презентація. Слайд 15)

Після побудови графіка функції у зошитах учням пропонується побудова на готовому рисунку.

 

г) Знайди відповідність. (Презентація. Слайд 16-17.)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

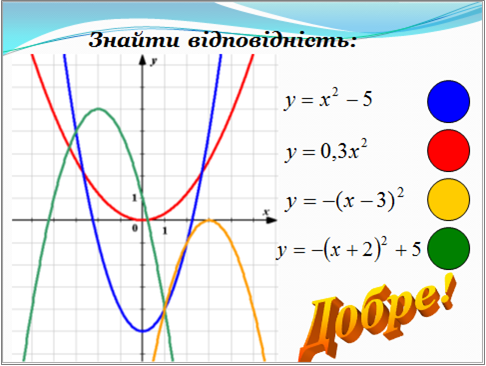
Використання мультимедійної дошки для побудови графіків функцій за допомогою паралельного перенесення.

 

 

 

 

   Робота в зошитах.№ 305, № 307 (по варіантах)

IV.  Побудова графіка квадратичної функції, та встановлення властивостей функції.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Самостійне виконання завдання в зошитах.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V.  Домашнє завдання. (Презентація. Слайд 17.)

 

VІ.   Підведення підсумків уроку.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розв’язування кросворду. (Презентація. Слайди 18 – 24.)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

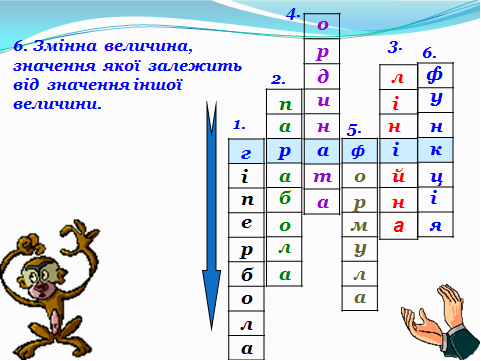
VІІ.   Висновок до уроку. (Презентація. Слайд 25.)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Учні разом із учителем аналізують роботу на уроці

(Презентація. Слайд 26.)