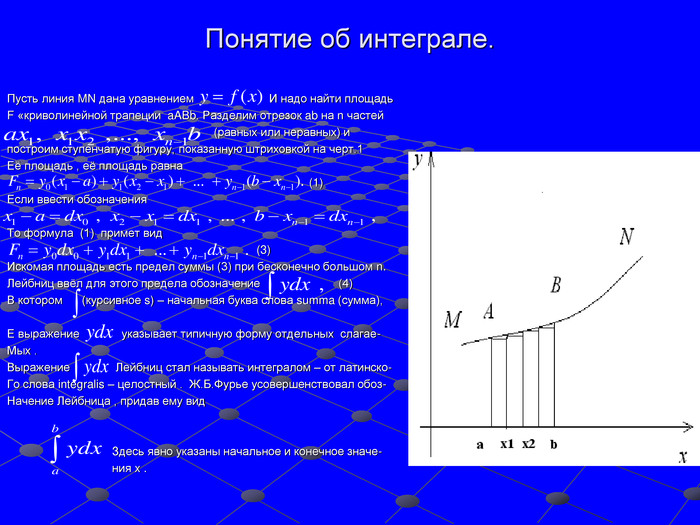
Тема кроку з алгебри: " Первісна та інтеграл ".
Про матеріал
В презентації є правила обчислення первісних та інтеграл. Показаний правила обчислення невизначеного та не визначеного інтегралів. Надані приклади з поясненням. Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра (академічний, профільний рівень) 11 клас (Нелін Є.П., Долгова О.Є.)
До уроку
§ 24. Первісна та її властивості Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку