Тема: Логарифмічна функція, її властивості та графік

Тема: Логарифмічна функція, її властивості та графік

Мета:

• ввести поняття логарифмічної функції, формувати вміння будувати графік логарифмічної функції, дослідити її властивості, познайомити учнів з використанням логарифмічної функції при вивченні явищ навколишнього світу;
• розвивати творче мислення, математичне мовлення;
• виховувати вміння працювати разом, почуття відповідальності, культуру спілкування.

Тип уроку: засвоєння нових знань і вмінь.

Обладнання: таблиці, комп’ютер, слайди, виконані в Power Point.

ХІД УРОКУ

І. Організаційний момент. Мотивація навчання

Підготовка учнів до уроку.

 – Сьогодні на уроці ми будемо говорити про такі речі:

Я розумію ваше здивування. Виникають запитання:

•               Що об’єднує ці малюнки?
•               Чому вони присутні у нас на уроці?
•               Як їх можна пов’язати з темами, що ми вивчаємо, і з математикою взагалі?

Але щоб все це пояснити, та докорінно у всьому розібратися, давайте пригадаємо основний матеріал, який ми вивчаємо.

ІІ. Перевірка домашнього завдання

Короткий аналіз після попередньої перевірки.

ІІІ. Актуалізація опорних знань

Питання до класу:

1. Що називається функцією? Наведіть приклади.

Залежність змінної у від змінної х називається функцією, якщо кожному значенню х відповідає єдине значення у.

2. Як називаються змінні х та у?

Х- незалежна змінна, аргумент;

У – залежна змінна, функція.

3. Яку функцію називають оборотною?

Функція f, яка має обернену, називається оборотною.

4. Назвіть достатню умову існування оберненої функції.

Достатньою умовою існування оберненої функції для даної функції є її монотонність, тобто зростання або спадання на всій області визначення.

5. Який існує алгоритм знаходження формули функції, оберненої до даної?

а) З’ясувати, чи є функція у = f(x) оборотною на всій області визначення. Якщо ні, то виділити проміжок, на якому функція монотонна;

б)  виразити х через у;

в)  поміняти позначення змінних.

6. Сформулюйте основні властивості взаємно обернених функцій.

а) Область визначення функції f співпадає з областю значень функції , і навпаки,  область значень функції f співпадає з областю визначення функції ;

б) якщо функція f зростає то і функція   зростає, якщо функція f спадає то і функція   спадає;

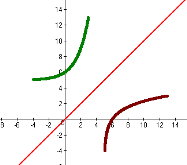
в) графіки функції , оберненої до функції f, симетричні графіку f відносно прямої .

7. Накресліть схематично графіки функцій та . Сформулюйте основні властивості показникової функції при основі

(Таблиця «Властивості показникової функції», ст. 21 проекту)

8. Дайте означення логарифма і сформулюйте його основні властивості.

Логарифмом числа за основою називається показник степеня , до якого треба піднести , щоб дістати .

якщо

якщо ;

якщо

якщо ;

якщо

ІV. Постановка мети уроку

Знання властивостей кожної з елементарних функцій значно спрощують розв’язування значної кількості  задач. В дослідженнях багатьох реальних процесів використовують функцію, обернену до показникової, яка називається логарифмічною. Тому перед нами виникає необхідність познайомитися з цією функцією та розглянути її властивості.

 Отже, тема нашого уроку «Логарифмічна функція та її властивості».

Ми повинні:

• розглянути поняття логарифмічної функції;
• навчитися будувати графік логарифмічної функції;
• дослідити її властивості;
• познайомитися з використанням логарифмічної функції в науці, техніці та природі.

V. Сприйняття й усвідомлення нового матеріалу

1. Поняття логарифмічної функції

 Розглянемо показникову функцію та знайдемо формулу оберненої до неї функції.

(Схема «Показникова функція => Логарифмічна функція», ст.24 проекту)

Логарифмічною називається функція , де , обернена до показникової

2. Графік логарифмічної функції.(Міні-дослідження)

 Для побудови графіка логарифмічної функції та формулювання її властивостей, я пропоную вам виконати такі завдання в групах:

І група Побудувати графік функції, оберненої до функції . (використовуючи властивості оберненої функції).

ІІ група Побудувати графік функції, оберненої до функції (використовуючи властивості оберненої функції).

ІІІ група Побудувати графік функції.

ІV група Побудувати графік функції.

3. Властивості логарифмічної функції.(Захист міні-проектів)

Властивості функції записані учнями кожної групи на плакаті. Аналізуємо властивості логарифмічної функції (в загальному вигляді), записуємо їх у зошит.

(Таблиця «Властивості логарифмічної функції», ст. 25 проекту)

4. Властивості логарифмів чисел

Проблемне питання: Як можна порівнювати логарифми чисел, використовуючи властивості логарифмічної функції?

Розгляньте завдання:

1. Порівняйте число з 1, якщо

  А. . Б.. В. . Г. .

2. Порівняйте числа і .

  А. . Б. . 

  В. . Г. .

3. Порівняйте числа .

  А. . Б. . 

  В.. Г. .

4. Порівняйте числа   і .

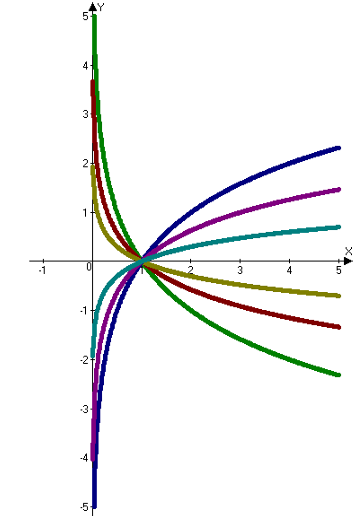 Щоб відповісти на ці питання, скористаємось результатами роботи творчої групи.

      (Короткий огляд результатів)

За допомогою графіків вказаних функцій спробуйте вдома вивести правила для порівняння логарифмів. Для цього вам слід заповнити наступну таблицю.

5. Застосування логарифмів та логарифмічної функції в науці, техніці та природі.

Виступ творчих груп (математиків, фізиків, біологів та хіміків) з презентацією свого дослідження.

(Застосування логарифмічної функції, ст. 26-30 проекту)

VІІ. Підсумок уроку

Питання до класу:

1. Яка функція є оберненою до показникової?
2. Яка функція називається логарифмічною?
3. При якій умові логарифмічна функція є зростаючою (спадною)?
4. Де використовується в навколишньому світі логарифмічна функція?

Оцінювання учнів.

VІІІ. Домашнє завдання

§22 Достатній рівень  № 215(1-2), 216 (1), 225(1-2);

 Високий рівень № 216,218, 227(2,7)