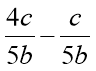Тема: «Основна властивість дробу. Додавання та віднімання дробів».
Алгебра. Клас: 8
Тема: «Основна властивість дробу. Додавання та віднімання дробів».
Мета: навчальна: повторення, узагальнення та систематизацію знань та вмінь, набутих учнями в ході вивчення теми; корекція знань учнів з урахуванням результатів самостійної роботи. Підготовка до тематичної контрольної роботи;
розвивальна: розвивати логічне, креативне мислення, пізнавальну активність; культуру математичного запису;
виховна: виховувати увагу, інтерес до математики.
Тип уроку: узагальнення та систематизація знань учнів з теми «Основна властивість дробу. Додавання та віднімання дробів»
ХІД УРОКУ
І. Організаційний момент.
ІІ. Перевірка домашнього завдання.
Аналіз самостійної роботи.
Звернути увагу учнів на:
- додавання і віднімання дробів з різними знаменниками;
- знаходження спільного знаменника і додаткових множників;
- розкладання многочлена на множники;
- ділення степенів.
Оскільки урок є останнім, підсумковим, то актуальним постає питання про повторення, узагальнення та систематизацію знань та вмінь, набутих учнями в ході вивчення теми.
ІІІ. Актуалізація опорних знань.
Фронтальне опитування.
З метою повторення теоретичного матеріалу, та для надання допомоги учням при засвоєнні знань, можна запропонувати їм систему питань:
1. Які вирази називаються цілими виразами? (Це вирази, що містять дії додавання, віднімання, множення, піднесення до степеня, а також ділення на число, відмінне від нуля.)
2. Які вирази називаються дробовими? (Це вирази, які містять дію ділення на вираз зі змінною).
3. Який дріб називається раціональним? (Дріб, який містить змінні у знаменнику)
4. Які значення змінних називають допустимими значеннями змінних у виразі? (Значення змінних, при яких можливі всі математичні дії, що містить раціональний вираз)
5. Сформулюйте основну властивість дробу. (Для будь-яких значень ![]() , де
, де ![]() , справедлива тотожність
, справедлива тотожність ![]() ).
).
6. Сформулюйте правила зміни знака перед дробом.
7. Як додати (відняти) дроби з однаковими знаменниками? (Щоб додати раціональні дроби з однаковими знаменниками, потрібно додати їх чисельники, а знаменники залишити без змін. Щоб відняти раціональні дроби з однаковими знаменниками, потрібно від чисельника зменшуваного відняти чисельник від’ємника, а знаменник залишити без змін).
8. Як звести дроби до найпростішого спільного знаменника? (Щоб звести дроби до найпростішого спільного знаменника, потрібно:
- знайти найпростіший спільний знаменник даних дробів;
- знайти для кожного дробу додатковий множник. Для цього потрібно спільний знаменник поділити на знаменники даних дробів;
- помножити чисельник кожного дробу на його додатковий множник;
- записати дроби із знайденими чисельниками та спільним знаменником.)
9. Як додати (відняти) дроби з різними знаменниками?
- знайти спільний знаменник дробів; звести дроби до спільного знаменника;
- знайти для кожного дробу додатковий множник; помножити чисельник кожного дробу на його додатковий множник;
- додати або відняти одержані дроби;
- спростити дріб, якщо це можливо.
Цілі і дробові вирази називаються раціональними виразами.
(Слайд 3)
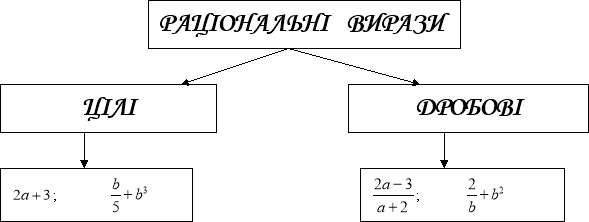
Розвиваємо креативне мислення
(Слайд 4)
- Який вираз пропущено
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()


- Відшукайте помилку.
(Слайд 5)
ІV. Закріплення знань
Робота в групах. (Слайд 6-11)
|
Картка І |
Картка ІІ |
|
1) При яких значеннях змінної не має змісту вираз
а) |
1) При яких значеннях змінної не має змісту вираз
а) |
|
2) Скоротити дріб:
а) |
2) Скоротити дріб:
а) |
|
3) Знайти значення виразу:
а)
|
3) Знайти значення виразу:
а) |
|
4) Відніміть дроби
|
4) Відніміть дроби
|
V. Повторення та систематизація знань
Розв’язування вправ.
Завдання 1. При яких значеннях змінної має смисл вираз:
а) ![]() .
.
Завдання 2. Скоротити дріб:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ;
;
5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() .
.
Завдання 3. Подати у вигляді дробу вираз:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
;
4) ![]() ; 5)
; 5) ![]() .
.
Завдання 4. Виконати дії:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
;
4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() .
.
Завдання 5. Довести тотожність:
(Слайд 13-15)
-
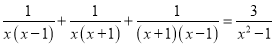 .
.
Розв’язання
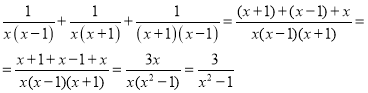
Розв’язання
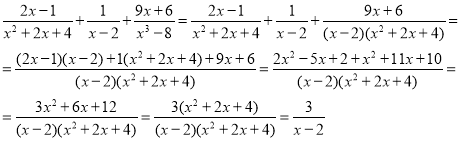
VІ. Підведення підсумків уроку.
Серед рівностей виберіть правильну. Поясніть свій вибір.
(Слайд 16)
-
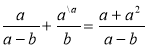 ;
;
-
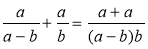 ;
;
-
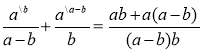 ;
;
Учитель відповідає на запитання учнів, а також аналізує успіхи учнів на уроці.
VІІ. Домашнє завдання.
Повторити: розділ 1, п. 1 – 4
Виконати вправи
ст.. 36 № 14; № 16
Додаток № 1
|
Картка І
|
|
1) При яких значеннях змінної не має змісту вираз
а)
|
|
2) Скоротити дріб:
а)
|
|
3) Знайти значення виразу:
а)
|
|
4) Відніміть дроби
|
|
Картка ІІ |
|
1) При яких значеннях змінної не має змісту вираз
а)
|
|
2) Скоротити дріб:
а)
|
|
3) Знайти значення виразу:
а)
|
|
4) Відніміть дроби
|
1


про публікацію авторської розробки
Додати розробку

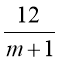 ; б)
; б) 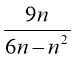 ?
?
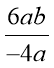 ; б)
; б) 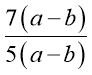
 , якщо
, якщо 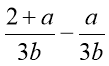
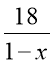 ; б)
; б) 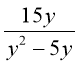 ?
?
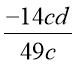 ; б)
; б) 
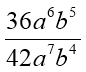 , якщо
, якщо 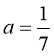 ;
;  ;
;