Тема. Розв’язування задач з кінематики

    Урок №5

Тема. Розв’язування задач

Мета. Формувати вміння розв’язувати

задачі з кінематики, виробляти навички застосовувати знання; розвивати вміння розв’язувати задачі, користуючись відомим матеріалом; ознайомити учнів з алгоритмом розв’язування задач з кінематики, раціональними методами розв’язування задач.

Тип уроку. Урок формування і застосування знань.

Девіз уроку. Якщо хочеш навчитись плавати, то сміливіше заходь у воду, а якщо хочеш розв’язувати задачі, то розв’язуй їх.

   Хід уроку.

І. Актуалізація опорних знань.

1. З’ясовуються “труднощі” при виконанні домашнього завдання.
2. Фізичний марафон “Чому?” (Фізичний марафон “Чому?” проводжу з учнями всього класу. Перший учень отримує картку з питаннями і швидко, без підготовки, дає відповідь на перше питання. Передає картку наступному учневі, який дає відповідь на слідуюче питання. Якщо учень не може дати відповідь, то на його питання відповідає слідуючий учень).

1. Чому фізика є наукою експерементальною?

(Тому що на основі спостережень і дослідів учені відкривають фізичні закони)

2. Чому одиниця швидкості (м/с) є похідною одиницею?

(Тому що вона складається з двох основних одиниць: метра і секунди)

3. Чому поняття “фізика” ширше, ніж поняття “механіка”?

(Тому що в поняття фізики входить, як його частина, механіка)

4. Чому знання кінематики потрібні людям, чия діяльність пов’язана з рухом тіл: водіям, морякам, пілотам?

(Тому що кінематика – частина механіки, в якій вивчають закони руху матеріальної точки, не розглядаючи причини, що викликають ці рухи)

5. Чому стіл у класі перебуває одночасно у спокої й у русі?

(Тому що відносно класу стіл нерухомий, а відносно Сонця рухається разом із Землею)

6. Чому практично неможливо вказати положення в просторі будь-якого досить об’ємного тіла?

(Тому що будь-яке тіло має незкінченну безліч точок, координати яких треба визначати, що просто неможливо, особливо, якщо тіло ще й рухається)

7. Чому величезне Сонце, довгий потяг, літак можна приймати за матеріальну точку?

(Тому що відстані, які вони проходять набагато більші, ніж їхні власні розміри)

8. Чому ковзаняра, який пробігає дистанцію в 10 км, можна вважати матеріальною точкою, а фігуриста, який виконує елемент фігурного катання обертання не можна?

( Тому що відстань, яку пробігає ковзаняр у багато разів більша, ніж розміри його власного тіла, а фігурист узагалі не переміщується)

9. Чому рух поршня у ДВЗ можна вважати поступальним рухом?

(Якщо на поршні подумки провести пряму, то в процесі руху вона залишається паралельною сама собі)

10. Чому механіка більш широке поняття, ніж кінематика?

(Тому що кінематика – це лише частина механіки)

11. Чому шлях, пройдений тілом під час руху –  скалярна величина?

(Тому що ця величина визначається лише числовим значенням)

12. Чому за такими, наприклад, даними “тіло вийшло з точки А і пройшло 2 км” не можна вказати, де перебуває тіло?

(Тому що невідомо в якому напрямі рухалося тіло)

13. Чому фізична величина переміщення – векторна величина?

(Тому що вона має напрям)

14. Чому часто буває так, що тіло рухалося і пройшло значний шлях, а його переміщення дорівнює нулю?

(Тому що тіло повернулося в ту саму точку з якої вийшло)

15. Чому не можна робити обчислення за формулами, записаними у векторній формі?

(Тому що будь-яка векторна величина визначається одночасно числовим значенням і напрямом у просторі)

16. Чому для повного опису руху даної матеріальної точки можна вибрати безліч систем відліку?

(Тому що будь-яке тіло рухається відносно безлічі інших тіл, які можна вибирати за тіло відліку і пов’язати цього із системою координат)

17. Чому відносний не лише механічний рух, а й спокій?

(Тому що, якщо, наприклад, два автомобілі рухаються поруч в одному напрямі з однаковою швидкістю, то відносно один одного вони перебувають у спокої)

18. Чому закон додавання швидкостей можна писати з двома знаками: (+) і (-)?

(Тому що в першому випадку обидва тіла переміщаються відносно один одного в протилежних напрямках, а в другому випадку – в одному напрямі)

19. Чому рівномірний рух є рухом зі сталою швидкістю?

(Тому що зміна часу в кілька разів у цтому русі спричинить пропорційну зміну переміщення, а їх відношення залишаться сталими)

20. Чому числове значення переміщення (модуль) лише в прямолінійному русі матеріальної точки може збігатися з числовим значенням пройденого шляху?

(Тому що в прямолінійному русі вектор переміщення збігається з пройденим шляхом, а в інших випадках вектор переміщення завжди менший, ніж пройдений шлях, тому що це найкоротша відстань від початку руху до його кінця)

ІІ. Об’явлення теми та очікуваних результатів.

  Тема сьогоднішнього уроку – “Розв’язування задач”. На ньому ви зможете: застосувати знання, отримані на попередніх уроках, при розв’язуванні задач; знаходити раціональні методи розв’язування задач.

ІІІ. Основний матеріал.

     Задача 1.

 Велосипедист і пішохід рухаються по дорозі до дерева, що росте на узбіччі. В початковий момент часу велосипедист знаходиться на відстані 18 м від дерева, а пішохід на відстані 6 м від дерева. Швидкість велосипедиста 6 м/с, пішохода – 1,2 м/с. За який час велосипедист і пішохід досягнуть дерева? За який час велосипедист дожене пішохода? Розв’язати задачу аналітичним, координатним іграфічним методами.

 Перш ніж ми почнемо розв’язувати задачу, я хочу звернути вашу увагу на пам’ятки які лежать у вас на партах.

   Пам’ятка

 Правила розв’язування задач з кінематики.

1. Уважно прочитайте задачу.
2. З’ясуй про що йдеться мова в задачі.
3. Визначити які величини відомі, а які треба знайти.
4. Запиши коротку умову.
5. Зроби схематичний малюнок, на якому покажи траєкторію руху точки, та вибери систему відліку.
6. Вкажи на малюнку всі кінематичні характеристики руху.
7. Запиши кінематичні рівняння у векторній формі, та в проекціях на вибрані осі координат.
8. Розв’яжи отриману систему рівнянь, та знайди шукану величину.
9. Зроби перевірку одиниць вимірювання.

10.Зроби відповідний висновок до задачі.

Повернемося до нашої задачі

(розв’язують учні методом “ланцюжка”)

   Розв’язання:

Дано: Аналітичний метод.

=6

       =1,2

S₁=18 м S₀

S₂=6 м                                 

x₀₁=18 м D  C

x₀₂=6 м  Х  

x₁=0 S₂  

x₂=0 S₁

x₁=x₂ 1. Якщо швидкість велосипедиста

t₁-? t₂-?       , а відстань від нього до             

t₃-? х₁(t)-?   дерева S₁=18 м і t₁- шуканий час руху,

х₂(t)-?          то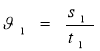                

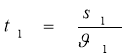
                     Підставляючи числові дані, дістаємо

  

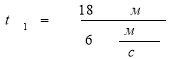
Аналогічно знаходимо час t₂ для руху пішохода до дерева:    ;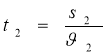 

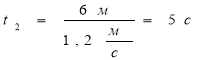
2. За час t  велосипедист проходить шлях S₁ , пішоход – шлях S₂ , причому

     ;                      

   У деякий момент часу  t= t₃  велосипедист дожене пішохода, шлях S₁ , пройдений велосипедистом, буде на S₀ =12 м більше від шляху S₂ , пройденого пішоходом:

      S₁ = S₂ + S₀ або · t₃ = ·t₂ + S₀

(S₀  - відстань між велосипедистом і пішоходом у початковий момент часу). Знайдемо час t₃ , за який велосипедист дожене пішохода:

 

      

   

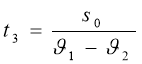
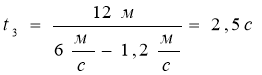
  За час t₃ = 2,5 с пішоход пройде відстань  від дерева S₃= ·t₃ ,

            S₃ =1,2·2,5с=3 м

 Таким чином, велосипедист дожене пішохода в точці D, що знаходиться на 3 м ліворуч від дерева.

   Координатний метод.

 1. Помістимо початок координат в точку С, де знаходиться дерево, і спрямуємо вісь вздовж дороги в напрямі руху. Тоді координати велосипедиста і пішохода в момент часу t = 0 (початкові координати)

  х₀₁ = -18 м,              х₀₂ = -6 м

Відповідні закони руху матимуть вигляд

 х₁ = х₀₁+·t,  х₂ = х₀₂+·t,

де і – проекції швидкостей велосипедиста і пішохода на вісь Х (для вибраного напряму осі Х ці проекції додатні)

 Маємо:

 х₁ = -18+6·t,  х₂ = -6+1,2·t,

 Час, коли велосипедист доїде до дерева, знаходимо з умови х₁=х_с=0. Звідки

 0 = -18+6·t₁,         t₁=3с

 Для пішохода час, коли він доїде до дерева, знаходимо з аналогічної умови               х₂=х_с=0, звідки

 0 = -6+1,2·t₂,   t₂=5с

 Час t₃ , за який велосипедист дожене пішохода, знаходимо з умови х₁=х₂ , оскільки в цей момент координати велосипедиста і пішохода однакові

 -18+6·t₃ =-6+1,2·t₃

 6·t₃ -1,2·t₃ =18-6

 t₃ =2,5с

 Підставимо знайдене значення t₃ =2,5с по черзі в кожне з рівнянь

 х₁ =-18м+6·2,5с=-3м;

 х₂ = -6м+1,2·2,5с=-3м.

    Графічний метод.

 Користуючись законами руху  х₁ = -18+6·t,   х₂=-6+1,2·t, побудуємо графік залежності х(t)

 

х₁ -18  -12  -6    0                 х₂   -6   -4,8  -3,6  –2,4   -1,2      0

t   0      1    2     3                            t     0     1      2     3       4         5

 

 

х,м

 

 

 

 

            1          2          3          4          5          6          7

 

                                                                                              t,с

                                А

-6

 

 

-12

 

 

-18

 Моменти часу, в які велосипедист і пішохід досягнуть дерева, знаходяться з умови х₁=0 або х₂=0.

Ці моменти часу визначаються перетином відповідного графіка х(t) з віссю абсцис. Як видно з графіка t₁=3с;  t₂=5с.

 Координату і момент часу, в якій велосипедист дожене пішохода, визначаємо як координату точки А перетину прямих 1 і 2. Бачимо, що точці А відповідають значення t₃=2,5с; х₃=-3с.

    Задача 2.

 Двома залізними коліями рухаються вантажний потяг і електричка. Швидкість вантажного потяга 36 км/год, електрички – 72 км/год, довжина потяга разом з вагонами 175 м, довжина електрички – 125 м. За який час вантажний потяг проїде повз пасажира електрички який дивиться на потяг у вікно вагона?

Дано:

=36=10

=72=20

L₁=180м

L₂=120м

t-?; t₁-?

 L₁  L₂

 

 У задачі потяги не можна розглядати як матеріальні точки, слід враховувати їхні розміри. В момент коли потяги розминуться, на одній лінії знаходитимуться їхні останні вагони. Відстань, яку потяги проходять один біля одного, дорівнює сумі їхніх довжин L₁ +L₂, а модуль швидкості V відн.  їхнього відносного руху дорівнює сумі модулей їхніх швидкостей відносно землі, відн = +. Тому час, за який потяги проходять один повз другого,

 L₁ +L₂

t =  ;

               +

 

           180м+120м 

t = .

            10 +20

 Знайдемо тепер час, за який потяг проходить повз пасажира електрички. У цьому випадку швидкість електрички відносно товарного потяга також дорівнює +, але пасажир “проходить” відносно товарного потяга шлях L₁ , що дорівнює довжині товарного потяга ( пасажира можна розглядати як матеріальну точку). Тому час руху пасажира відносно товарного потяга або, що те саме, товарного потяга відносно пасажира:

 L₁  

t₁ =  ;

            +

t₁=6с.

ІV.   Підсумок (Рефлексія).

 (Учитель коментує роботу учнів, та оцінює її)

 Наш урок закінчився.

Що вам найбільше сподобалося сьогодні на уроці? Чому?

Що не сподобалося? Чому?

5. Домашнє завдання.

Повторити конспекти лекцій

Задача.

       Ескалатор метро піднімає стоячу на ньому людину за t₁=1хв; якщо ескалатор не рухається, а людина піднімається по ньому сама, на підйом затрачується t₂=3хв. Скільки часу затратиться на підйом, якщо людина буде підніматися по рухомому ескалатору?