Тематичне

оцінювання

з математики

8 клас

 

8 клас (алгебра)

 

ТО №12. „Скорочення, додавання і віднімання раціональних виразів”.

І варіант

І рівень

1. Обчислити значення дробу: , якщо .

2. Виконай дії:   а) ;    б) .
II рівень

3. Знайти допустимі значення змінної виразу: .

4. Скоротити дроби:

           а) ;  б) ;  в) .

ІІІ рівень

5. Виконати додавання і віднімання:

   а) ;  б) ;

               в)

IV рівень

6. Спростити вираз:   

               .

7. Скоротити дріб:  .

 

ІІ варіант

І рівень

1. Обчислити значення дробу: , якщо .

 

2. Виконай дії:   а) ;    б) .
II рівень

3. Знайти допустимі значення змінної виразу: .

 

 

4. Скоротити дроби:

           а) ;  б) ;  в) .

ІІІ рівень

5. Виконати додавання і віднімання:

   а) ;  б) ;

               в)

IV рівень

6. Спростити вираз:   

               .

7. Скоротити дріб:  .

 

ІІІ варіант

І рівень

1. Обчислити значення дробу: , якщо .

2. Виконай дії:   а) ;    б) .
II рівень

3. Знайти допустимі значення змінної виразу: .

4. Скоротити дроби:

           а) ;  б) ;  в) .

ІІІ рівень

5. Виконати додавання і віднімання:

   а) ;  б) ;

               в)

IV рівень

6. Спростити вираз:   

               .

7. Скоротити дріб:  .

 

ІV варіант

І рівень

1. Обчислити значення дробу: , якщо .

2. Виконай дії:   а) ;    б) .
II рівень

3. Знайти допустимі значення змінної виразу: .

 

4. Скоротити дроби:

           а) ;  б) ;  в) .

ІІІ рівень

5. Виконати додавання і віднімання:

   а) ;  б) ;

               в)

IV рівень

6. Спростити вираз:   

               .

 

7. Скоротити дріб:  .

 

 

ТО №2. „Множення і ділення раціональних виразів. Степінь з цілим показником”.

I варіант

І рівень

1. Чому дорівнює степінь з нульовим показником?

2. Сформулюйте правило множення дробів.

3. Виконати дію: .

ІІ рівень

4. Виконати множення і ділення дробів:

     а) ;   б) .

5. Записати числа в стандартному вигляді:

    а) 49000000; б) 0,0067.

ІІІ рівень

6. Спростити вираз: .

7.   Виконати дії над числами:

    а)  ;  б) .

IV рівень

8. Доведіть тотожність:

       .

 

 

ІI варіант

І рівень

1. Яке правило піднесення до степеня?

 

2. Сформулюйте правило ділення дробів.

3. Виконати дію: .

ІІ рівень

4. Виконати множення і ділення дробів:

     а) ;   б) .

5. Записати числа в стандартному вигляді:

    а) 380000; б) 0,0000121.

ІІІ рівень

6. Спростити вираз: .

 

7.   Виконати дії над числами:

  а)  ; б) .

IV рівень

8. Доведіть тотожність:

       .

 

ІІI варіант

І рівень

1. Яке правило ділення  степенів?

2. Сформулюйте правило ділення дробів.

3. Виконати дію: .

ІІ рівень

4. Виконати множення і ділення дробів:

     а) ;   б) .

5. Записати числа в стандартному вигляді:

    а) 54000; б) 0,000071.

ІІІ рівень

6. Спростити вираз: .

7.   Виконати дії над числами:

    а)  ;  б) .

IV рівень

8. Доведіть, що значення виразу не залежить від змінної:

       .

ІV варіант

І рівень

1. Чому дорівнює степінь з нульовим показником?

2. Сформулюйте правило множення дробів.

3. Виконати дію: .

ІІ рівень

4. Виконати множення і ділення дробів:

     а) ;   б) .

5. Записати числа в стандартному вигляді:

    а) 4700000; б) 0,000000082.

ІІІ рівень

6. Спростити вираз: .

7.   Виконати дії над числами:

    а)  ;  б) .

IV рівень

8. Доведіть тотожність:

                  .

 

ТО № 3. „Квадратні корені”.

І варіант

І рівень

1. Коренем з числа називається...

2. Корінь з добутку дорівнює...

3. Обчислити:  .

ІІ рівень

4. Знайти значення виразів:

    а) ; б) ;  в) ;  г) .

5. Розв’язати рівняння:   .

ІІІ рівень

6. Виконати дії:

   а) ;                   б) ;

   в) ;  г) .

7. Виконати дії з дробами:  .

ІV рівень

8. Скоротити дріб:   .

9. Спростити вираз:   .

 

 

 

ІІ варіант

І рівень

1. Рівняння має розв’язки...

2. Корінь з дробу дорівнює...

3. Обчислити:  .

ІІ рівень

4. Знайти значення виразів:

 

    а) ; б) ;  в) ;  г) .

5. Розв’язати рівняння:   .

ІІІ рівень

6. Виконати дії:

   а) ;                   б) ;

   в) ;       г) .

7. Виконати дії з дробами:  .

ІV рівень

8. Скоротити дріб:   .

9. Спростити вираз:   .

 

 

ІІІ варіант

І рівень

1. Квадратний корінь має зміст...

2. ;    

3. Обчислити:  .

ІІ рівень

4. Знайти значення виразів:

    а) ; б) ;  в) ;  г) .

5. Розв’язати рівняння:   .

ІІІ рівень

6. Виконати дії:

   а) ;                   б) ;

   в) ;           г) .

 

7. Виконати дії з дробами:  .

ІV рівень

8. Скоротити дріб:   .

9. Спростити вираз:   .

 

 

ІV варіант

І рівень

1. Квадратний корінь не має змісту...

2. Корінь з добутку дорівнює...

3. Обчислити:  .

ІІ рівень

4. Знайти значення виразів:

    а) ; б) ;  в) ;  г) .

5. Розв’язати рівняння:   .

ІІІ рівень

6. Виконати дії:

   а) ;                 б) ;

   в) ;  г) .

7. Виконати дії з дробами:  .

ІV рівень

8. Скоротити дріб:   .

9. Спростити вираз:   .

 

ТО № 4. “Квадратні рівняння”.

І варіант

І рівень

1. Квадратним рівнянням називається рівняння  виду …
2. Теорема Вієта формулюється так: …
3. З даних рівнянь вибрати неповне квадратне:

5х² + 6х – 8 = 0; х² – х – 4 = 0; 2х – 7 = 0;

4х² – 100 = 0;  х² – 10х + 1 = 0.

ІІ рівень

4. Розв’язати неповні квадратні рівняння:

а) 7х² – 5х = 0;   б) 3х² – 108 = 0.

5. Розв’язати рівняння за формулою коренів:

                        2х² – 7х + 6 = 0.

6. Розв’язати рівняння за теоремою Вієта:

                        х² – 12х + 35 = 0.

ІІІ рівень

7. Знайти корені рівняння:

                          2у · ( 3у + 4 ) = 4у² + 5у + 27.

8. Площа прямокутника 88 см². Знайти сторони прямокутника, якщо одна з них на 3 см більша за другу.

IV рівень

9. Скласти квадратне рівняння, якщо його корені   –3; 1.
10. Відомо, що х₁ і х₂ – корені рівняння  х² – 9х + 5 = 0. Не розв’язуючи рівняння  знайти значення виразу х₁² + х₂².

 

 

ІІ варіант

І рівень

1. Квадратне рівняння називається неповним, якщо …
2. Якщо дискримінант дорівнює нулю, то рівняння …
3. З даних рівнянь вибрати повне квадратне:

5х² – 8х + 5 = 0; 5х² + х – 6 = 0; 9х – 10 = 0;

2х² + 15 = 0;  4х² – 10х = 0.

ІІ рівень

4. Розв’язати неповні квадратні рівняння:

а) 9х² – 10х = 0;   б) 4х² – 100 = 0.

5. Розв’язати рівняння за формулою коренів:

                        9у² – 13у + 4 = 0.

6. Розв’язати рівняння за теоремою Вієта:

                        х² – 5х – 24 = 0.

ІІІ рівень

7. Знайти корені рівняння:

                          ( х – 3 )² = 2 ( х + 1 ).

8. Площа прямокутної ділянки 270 м². Знайти сторони ділянки, якщо одна з них на 3 м менша за другу.

IV рівень

9. Скласти квадратне рівняння, якщо його корені   5; 3.
10. Різниця  коренів  квадратного рівняння  х² + 5х + с = 0  дорівнює 3. Знайти с.

 

ІІІ варіант

І рівень

1. Квадратне рівняння називається зведеним, якщо …
2. Квадратне рівняння має два корені, якщо …
3. З даних рівнянь вибрати неповне квадратне:

9х² – 7х + 1 = 0; 9х² – 7х = 0; 9х + 1 = 0;

х² – 7х + 4  = 0;  3х² – 10 = 0.

ІІ рівень

4. Розв’язати неповні квадратні рівняння:

а) 5х² – 6х = 0;   б) 150 – 6х² = 0.

5. Розв’язати рівняння за формулою коренів:

                        4х² – 19х + 12 = 0.

6. Розв’язати рівняння за теоремою Вієта:

                        у² + 5у – 14 = 0.

ІІІ рівень

7. Знайти корені рівняння:

                          3х² – 8 = ( х + 4 )².

8. Площа прямокутника 112 см². Знайти сторони прямокутника, якщо одна з них на 9 см більша за другу.

IV рівень

9. Скласти квадратне рівняння, якщо його корені  2; – 5.

 

10. Відомо, що х₁ і х₂ – корені рівняння  х² + 5х – 8 = 0. Не розв’язуючи рівняння  знайти значення виразу х₁² + х₂².

 

IV варіант

І рівень

1. Дискримінант квадратного рівняння обчислюється за формулою…
2. Квадратне рівняння немає коренів, якщо …
3. З даних рівнянь вибрати зведене рівняння:

6х² – 4х –8 = 0; 6х² – 8 = 0; х² – 4х – 8 = 0;

6х² – 4х = 0;  4х – 10 = 0.

ІІ рівень

4. Розв’язати неповні квадратні рівняння:

а)  10х – 11х² = 0;   б) 5х² – 80 = 0.

5. Розв’язати рівняння за формулою коренів:

                        2х² – 7х – 30 = 0.

6. Розв’язати рівняння за теоремою Вієта:

                        х² + 3х – 28 = 0.

ІІІ рівень

7. Знайти корені рівняння:

                         3х ( 5х + 3 ) = 2х ( 6х + 5 ) + 2 .

8. Площа прямокутної ділянки 70 м². Знайти сторони ділянки, якщо одна з них на 3 м менша за другу.

IV рівень

9. Скласти квадратне рівняння, якщо його корені   7; 4.
10. Різниця  коренів  квадратного  рівняння   х² – 7х + с = 0  дорівнює 1. Знайти с.

 

 

 

 

ТО № 5. “Розв’язування рівнянь і задач, що зводяться до квадратних”.

І варіант

І рівень

1. Яке рівняння називається біквадратним?
2. Продовжити розв’язування рівняння:

 

                   у³ – 7у² + 10у = 0

                  у · ( у² – 7у + 10 ) = 0 …

ІІ рівень

3. Розв’язати рівняння 

                 ( у² – 1 )² – 10 · ( у² – 1 ) + 9 = 0

      ввівши заміну х = у² – 1.

4. Розв’язати біквадратне рівняння:

                    4х⁴ + 7х² – 2 = 0.

ІІІ рівень

5. Знайти розв’язки рівняння:

         .

IV рівень

6. Відстань між двома станціями дорівнює 200 км. Електропоїзд прибув до другої станції і знову повернувся на першу станцію, витративши на це 9 год. З якою швидкістю рухався електропоїзд до другої станції, якщо назад він повертався з швидкістю на 10 км/год більшою, ніж початкова?

 

ІІ варіант

І рівень

1. Яке рівняння називається дробовим раціональним?
2. Продовжити розв’язування рівняння:

                   х³ + 5х² + 6х = 0

                  х · ( х² + 5х + 6 ) = 0 …

ІІ рівень

3. Розв’язати рівняння 

                 ( х² – 9 )² – 8 · ( х² – 9 ) + 7 = 0

      ввівши заміну у = х² – 9.

4. Розв’язати біквадратне рівняння:

                    у⁴ + 5у² – 36 = 0.

ІІІ рівень

5. Знайти розв’язки рівняння:

             .

IV рівень

6. Відстань між двома пристанями 180 км. Моторний човен подолав її туди і назад за 11 годин. Знайти власну швидкість човна, якщо швидкість течії річки 3 км/год?

 

ІІІ варіант

І рівень

1. Яке рівняння називається біквадратним?
2. Продовжити розв’язування рівняння:

                   у³ – 9у² + 14у = 0

                  у · ( у² – 9у + 14 ) = 0 …

ІІ рівень

3. Розв’язати рівняння 

                 ( у² + 3 )² – 11 · ( у² + 3 ) + 28 = 0

      ввівши заміну х = у² + 3.

4. Розв’язати біквадратне рівняння:

                    5х⁴ – 4х² – 1 = 0.

ІІІ рівень

5. Знайти розв’язки рівняння:

           .

IV рівень

6. Моторний човен пройшов 24 км за течією річки і 40 км проти течії, затративши на весь шлях 7 годин. Знайти швидкість моторного човна в стоячій воді, якщо швидкість течії річки

      2 км/год?

 

IV варіант

І рівень

1. Які є способи розв’язування рівнянь вищих порядків?
2. Продовжити розв’язування рівняння:

                   х³ – 5х² + 4х = 0

                  х · ( х² – 5х + 4 ) = 0 …

ІІ рівень

3. Розв’язати рівняння 

                ( х² – 2 )² – 9 · ( х² – 2 ) + 14 = 0

      ввівши заміну у = х² – 2.

4. Розв’язати біквадратне рівняння:

                    у⁴ – 10у² + 9 = 0.

ІІІ рівень

5. Знайти розв’язки рівняння:

      .

IV рівень

6. Відстань від міста до села 120 км. Велосипедист, збільшивши швидкість на 4 км/год, прибув до села на 1 год швидше розкладу. З якою швидкістю рухався велосипедист?

 

 

 

 

 

 

 

 

 

 

Підсумкова контрольна робота

І варіант

І рівень

1) Знайти значення виразу , якщо .

2.    Обчислити  .
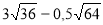3.    Скоротити дріб  .

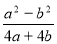ІІ рівень

4.    Виконати множення   .   

 

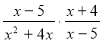5.    Розв'язати рівняння .

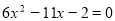ІІІ рівень

6.    Спростити вираз  .
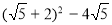7.    Доведіть тотожність:    .

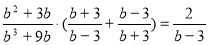IV рівень

8. 3 одного міста в інше, відстань між якими дорівнює 300 км виїхали дві машини. Одна з них рухалась зі швидкісно на 10 км/год більшою ніж друга, а тому прибула до пункту  призначення  на годину раніше за другу. Знайти швидкість кожної машини.

 

ІІ варіант

І рівень

1) Знайти значення виразу , якщо .

2) Обчислити  .

3) Скоротити дріб  .

ІІ рівень

4. Виконати множення   .   
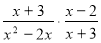5. Розв'язати рівняння .

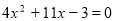ІІІ рівень

6. Спростити вираз  .
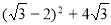7. Доведіть тотожність:   .

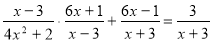IV рівень

8. 3 одного міста в інше, відстань між якими дорівнює 240 км виїхали одночасно автобус і автомобіль. Автобус, рухаючись зі швидкістю на 20 км/год меншою ніж автомобіль, прибув до пункту призначення на годину пізніше. Знайти швидкість автомобіля і автобуса.

 

 

 

 

 

 

8 клас (геометрія)

 

ТО №1: “Чотирикутники”.

І варіант

І рівень

1. Що таке діагоналі чотирикутника?
2. Що таке паралелограм?
3. Записати властивості прямокутника.

ІІ рівень

4. Один з куті ромба 162. Знайти решта кути ромба.
5. Одна сторона паралелограма 26 см, а друга на 14 см менша. Знайти периметр паралелограма.

ІІІ рівень

6. Сума кутів паралелограма 246. Знайти кути паралелограма.
7. Один з кутів ромба у 5 разів більший від другого. Знайти кути ромба.

IV рівень

8. Різниця двох сторін прямокутника 24 см. Знайти периметр прямокутника, якщо сторони відносяться як 3 : 7.

 

ІІ варіант

І рівень

1. Які сторони чотирикутника називаються сусідніми?
2. Ромбом називається…
3. Записати властивості квадрата.

ІІ рівень

4. Один з куті ромба 148. Знайти решта кути ромба.
5. Периметр паралелограма 50 см, менша сторона 10 см. Знайти довжину більшої сторони.

ІІІ рівень

6. Сума двох кутів паралелограма 226. Знайти кути паралелограма.
7. Один з кутів ромба на 56 більший від другого. Знайти кути ромба.

IV рівень

8. Сторони прямокутника відносяться як 5 : 11. Знайти сторони прямокутника, якщо периметр 96 см.

 

ІІІ варіант

І рівень

1. Сусідніми називаються вершини…
2. Що таке прямокутник?
3. Записати властивості ромба.

ІІ рівень

4. Один з куті паралелограма 78. Знайти решта кути паралелограма.
5. Одна сторона прямокутника 20 см, а друга на 4 см більша. Знайти сторони прямокутника і периметр.

ІІІ рівень

6. Сума двох кутів ромба 164. Знайти кути ромба.
7. Різниця двох кутів паралелограма 54.  Знайти кути паралелограма.

IV рівень

8. Одна із сторін прямокутника на 21 см менша від другої. Знайти сторони, якщо периметр дорівнює 62 см.

 

 ІV варіант

І рівень

1. Які вершини називаються протилежними?
2. Що таке квадрат?
3. Записати властивості паралелограма.

ІІ рівень

4. Один з куті паралелограма 63. Знайти решта кути паралелограма.
5. Периметр прямокутника 26 см, більша сторона 8 см. Знайти довжину меншої сторони.

ІІІ рівень

6. Сума двох кутів ромба 108. Знайти кути ромба.

 

7. Різниця двох кутів паралелограма 38.  Знайти кути паралелограма.

IV рівень

8. Сторони паралелограма відносяться як 8 : 3. Знайти периметр паралелограма, якщо більша сторона 32 см.

 

 

ТО №2. “Трапеція. Теорема Фалеса.”

1. Запишіть теорему Фалеса,
2. Якщо основи 7 см і 13 см, то середня лінія трапеції дорівнює...

3. Кут при одній з основ рівнобічної трапеції дорівнює 65°. Знайдіть решту кутів трапеції.
4. Середня лінія трапеції 14 см, а одна з основ 8 см. Знайдіть другу основу трапеції.

5. Один з кутів рівнобічної трапеції на 26° більший від другого. Знайти куги трапеції.
6. Висота  рівнобічної трапеції поділяє більшу основу на відрізки 8 см і 28 см. Знайти середню лінію трапеції.

1. Який чотирикутник називається трапецією?
2. Якщо основи 6 см і 14 см, то середня лінія трапеції дорівнює...

3. Кут при одній з основ рівнобічної трапеції дорівнює 134°. Знайдіть решту кутів трапеції.
4. Середня лінія трапеції 16 см, а одна з основ 20 см. Знайдіть другу основу трапеції.

5. Один з кутів рівнобічної трапеції у 4 рази більший від другого. Знайти кути трапеції.
6. Висота  рівнобічної трапеції поділяє більшу основу на відрізки 6 см і 26 см. Знайти середню лінію трапеції.

7. Діагональ трапеції ділить її середню лінію на два відрізки, один з яких на. 5 см менший від другого. Знайдіть основи трапеції, якщо середня лінія 25 см.

 

1. Запишіть властивість середньої лінії трикутника.
2. Якщо основи 8 см і 12 см, то середня лінія трапеції дорівнює...

3. Кути при одній з основ трапеції дорівнюють 55º,  83°. Знайдіть решту кутів трапеції,
4. Основа рівнобедреного трикутника 12 см. Знайдіть середню лінію трикутника, що сполучає бічні сторони.

5. Один з кутів рівнобічної трапеції на 54° менший від другого. Знайти кути трапеції.
6. Діагональ рівнобічної трапеції є бісектрисою тупого кута. Знайти периметр трапеції, якщо основи 6 см і 10 см.

 

1. Запишіть властивість середньої лінії трапеції.
2. Якщо основи 4 см і 16 см, то середня лінія трапеції дорівнює...

3. Кути при одній з основ трапеції дорівнюють 122º і 148°. Знайдіть решту кутів трапеції.
4. Основа рівнобедреного трикутника 18 см. Знайти середню лінію трикутника, що сполучає бічні сторони.

5. Кути рівнобічної трапеції відносяться як 2 : 7. Знайти кути трапеції.
6. Діагональ рівнобічної трапеції є бісектрисою гострого кута. Знайти периметр трапецій якщо основи 5 см і 8 см.

Середня  лінія  трапеції  22 см,  а  одна  з її основ менша від другої на 12 см. Знайдіть основи трапеції.

 

ТО № 3. „Подібність трикутників.”

І варіант

І рівень

1. Сформулювати ІІІ ознаку подібності трикутників.
2. Дуга кола дорівнює …
3. Катет прямокутного трикутника є середнє пропорційне …

ІІ рівень

4. Чи  подібні  ∆OSR  і  ∆O₁S₁R₁,  якщо  OS = 16 см, SR = 30 см, OR = 39 см, O₁S₁ = 8 см, S₁R₁ = 10 см, O₁R₁ = 13 см.
5. У трикутнику сторони дорівнюють 12 см, 16 см, 20 см, а у подібного трикутника найменша сторона 48 см. Знайти сторони подібного трикутника.

ІІІ рівень

6. На колі взято точки А, В, С, дуга АС = 80°. Знайти величину кута АВС.
7. Сторони трикутника відносяться як 3 : 4 : 7. Знайти сторони подібного трикутника, у якого периметр 98 см.

IV рівень

8. Сторони трикутника 25 см, 39 см, 40 см. Обчислити довжину відрізків, на які ділить сторону бісектриса кута утвореного найбільшою і найменшою стороною.

 

 

ІІ варіант

І рівень

1. Сформулювати І ознаку подібності трикутників.
2. Який кут називається вписаним в коло? Намалюй його.
3. Висота прямокутного трикутника проведена з вершини прямого кута є …

ІІ рівень

4. Чи подібні ∆KMN і ∆K₁M₁N₁ , якщо KM = 22 см, MN = 39 см, KN = 30 см, K₁M₁ = 11 см,  M₁N₁ = 13 см, K₁N₁ = 15 см.

 

5. У трикутнику сторони дорівнюють 42 см, 45 см, 51 см, а у подібного трикутника найбільша сторона 17 см. Знайти сторони подібного трикутника.

ІІІ рівень

6. На колі взято точки А, М, D, дуга АD = 140°. Знайти величину кута АМD.
7. Сторони трикутника 12 см, 13 см, 15 см. Знайти сторони подібного трикутника, у якого різниця найбільшої і найменшої сторін 9 см.

IV рівень

8. Різниця двох сторін трикутника 15 см, а бісектриса кута між ними ділить третю сторону на відрізки 15 см і 24 см. Знайти сторони трикутника.

 

ІІІ варіант

І рівень

1. Які фігури називаються подібними?
2. Що таке центральний кут? Намалюй його.
3. Катет прямокутного трикутника є середнє пропорційне …

ІІ рівень

4. Чи  подібні  ∆АВС  і  ∆А₁В₁С₁,  якщо  АВ = 9 см, ВС = 11 см, АС = 15 см, А₁В₁ = 18 см, В₁С₁ = 22 см, А₁С₁ = 30 см.
5. У трикутнику сторони дорівнюють 6 см, 9 см, 14 см, а у подібного трикутника найменша сторона 54 см. Знайти сторони подібного трикутника.

ІІІ рівень

6. На колі взято точки Р, Т, D, дуга PD = 100°. Знайти величину кута PTD.
7. Сторони трикутника 12 см, 13 см, 15 см. Знайти сторони подібного  трикутника, у якого сума найменшої і найбільшої сторін 54 см.

IV рівень

8. Сторони трикутника 15 см, 20 см, 30 см. Обчислити довжину відрізків, на які ділить бісектриса трикутника меншу сторону.

 

 

ІV варіант

І рівень

1. Сформулювати ІІ ознаку подібності трикутників.
2. Вписаний у коло кут дорівнює …
3. Бісектриса трикутника ділить протилежну сторону …

ІІ рівень

4. Чи  подібні  ∆CDP  і  ∆C₁D₁P₁,  якщо  CD = 12 см, DP = 14 см, СP = 18 см, C₁D₁ = 48 см,  D₁P₁ = 56 см, C₁P₁ = 72 см.
5. У трикутнику сторони дорівнюють 50 см, 70 см, 75 см, а у подібного трикутника середня за величиною сторона 14 см. Знайти сторони подібного трикутника.

ІІІ рівень

6. На колі взято точки M, N, D, дуга MD = 120°. Знайти величину кута MND.
7. Сторони трикутника 12 см, 14 см, 16 см. Знайти сторони подібного трикутника, у якого периметр 84 см.

IV рівень

8. Дві сторони трикутника 25 см і 40 см, а бісектриса кута між ними ділить третю сторону на відрізки, різниця між якими 9 см. Знайти третю сторону трикутника.

 

 

 

 

ТО № 4. „Теорема Піфагора

Співвідношення в прямокутному трикутнику”.

І варіант

          А                                                                              

                                                   

 

5. У  рівнобедреному трикутнику кут при основі дорівнює 30°, а основа 46 см. Знайти бічну  сторону трикутника.
6. У прямокутному трикутнику катети відносяться як 4 : 3, а гіпотенуза дорівнює 65 см. Знайти периметр трикутника.

7. У рівнобічній трапеції більша основа дорівнює 108 см, а бічна сторона і висота відповідно дорівнюють 58 см і 40 см. Знайти периметр
   трапеції.

 

 

 

II варіант

І рівень

1. Намалювати прямокутний трикутник АРD з катетами АР і РD.

2.  Заповнити пропуски користуючись малюнком

 

         M    

          C                                  N

 

 

3. Катет, що лежить проти кута α дорівнює ...
ІІ рівень

III рівень

5. У  рівнобедреному  трикутнику  основа дорівнює  60 см, а висота, проведена до основи 16 см. Знайти бічну сторону трикутника.
6. У прямокутному трикутнику катети відносяться як 3 : 4, а гіпотенуза дорівнює 55 см. Знайти периметр трикутника.

IV рівень

 

2.  Заповнити пропуски користуючись малюнком    

                   R

         A                                   P

3. Катет, що прилягає до кута α дорівнює ...

 

 

II рівень

4. У прямокутному трикутнику один з катетів дорівнює 34 см, а

      кут, що прилягає до нього 52°. Знайти невідомий кут і сторони.

7. У  рівнобічній  трапеції  основи  дорівнюють 12 см і 28 см, а кут при основі 30°. Знайти висоту трапеції і її периметр.

 

 

 

IV варіант

І рівень

2.  Заповнити пропуски користуючись малюнком

            K

                                   

            

            B                D

3. Катет, що прилягає до кута α дорівнює ...

II рівень

III рівень

5. У рівнобедреному трикутнику кут при основі дорівнює 30°, а бічна сторона 16 см. Знайти основу трикутника.
6. У прямокутному трикутнику один з катетів відноситься до гіпотенузи як 3 : 5, а другий катет 60 см. Знайти периметр трикутника.

IV рівень

7.   У прямокутній трапеції більша бічна сторона 16 см, менша основа 10 см, кут при основі 120°. Знайти периметр трапеції.

 

 

 

ТО № 5. “Площі фігур”.

І варіант

І рівень

1. Записати формули для обчислення площі паралелограма.
2. S = ¹/₂d²sinα . Формула площі якої фігури записана?
3.    B                C

                                   ABCD – квадрат, АВ = 8 см.       

                                   Знайти S_квадр.

         А                D

ІІ рівень

4. Знайти  площу  трапеції,  якщо  її  основи 4 дм і 12 дм, а висота 6 дм.
5. Сторони трикутника дорівнюють 17 см, 65 см, 80 см. Знайти радіус кола, описаного навколо трикутника.

 ІІІ рівень

6. Сторони прямокутника відносяться як 3 : 5, а його площа дорівнює 240 см². Знайти периметр прямокутника.

IV рівень

7. У рівнобічній трапеції основи і висота відносяться як 3 : 7 : 5, а діагональ дорівнює 25 см. Знайти площу трапеції.

 

 

 

ІІ варіант

І рівень

1. Записати формули для обчислення площі прямокутника.
2. S = ¹/₂absinα . Формула площі якої фігури записана?

 

3.    B                К       C

                                          ABCD – паралелограм,

                                          ВС = 25 см, DК = 8 см.       

 А                            D        Знайти S_парал.

ІІ рівень

4. Катети прямокутного трикутника дорівнюють 9 см і 10 см. Знайти його площу.
5. Сторони трикутника дорівнюють 35 см, 29 см, 8 см. Знайти радіус кола, вписаного в трикутник.

 ІІІ рівень

6. У паралелограмі бісектриса гострого кута, що дорівнює 30°, ділить його сторону на відрізки 24 см і 16 см, починаючи від вершини тупого кута. Знайти площу паралелограма.

IV рівень

7. У рівнобічній трапеції різниця основ 16 см, а периметр – 52 см. Знайти площу трапеції, якщо бічна сторона і висота відносяться як 13 : 5.

 

ІІІ варіант

І рівень

1. Записати формули для обчислення площі трикутника.
2. S = а²sinα . Формула площі якої фігури записана?
3.    B               

                                   ABC – трикутник, BD = 7 см,      

                                    АС = 12 см.   Знайти S_.

   А      D                С

ІІ рівень

4. Знайти площу ромба, якщо його діагоналі 7 см і 10 см.
5. Сторони трикутника дорівнюють 13 см, 14 см, 15 см. Знайти радіус кола, описаного навколо трикутника.

 

ІІІ рівень

6. Площа ромба 640 см², а діагоналі відносяться як 4 : 5. Знайти периметр ромба.

IV рівень

7. У рівнобічній трапеції різниця основ дорівнює 36 см, а периметр 128 см. Знайти площу трапеції, якщо її бічна сторона і висота відносяться як 5 : 4.

 

ІV варіант

І рівень

1. Записати формули для обчислення площі ромба.
2. S = ¹/₂d² . Формула площі якої фігури записана?
3.    B                         C

                                          ABCD – паралелограм,

                                          ВА = 10 см, AD = 19 см,

                                           А = 30°.       

 А                            D        Знайти S_парал.

ІІ рівень

4. Знайти площу прямокутника, якщо його сторони 9 см і 12 см.
5. Сторони трикутника дорівнюють 15 см, 13 см, 4 см. Знайти радіус кола, вписаного в трикутник.

 ІІІ рівень

6. У паралелограмі бісектриса тупого кута, що дорівнює 150°, ділить його сторону на відрізки 25 см і 15 см, починаючи від вершини гострого кута. Знайти площу паралелограма.

IV рівень

7. У рівнобічній трапеції основи і висота відносяться як 13 : 5 : 3, а бічна сторона 35 см. Знайти площу трапеції.

 

 

 

 

 

Підсумкова контрольна робота

І варіант

1. У ромба протилежні...
2. Квадрат гіпотенузи дорівнює ...
3. Катет, що лежить проти куга а дорівнює...

ІІ рівень

4. Один з кутів ромба – 78. Знайти невідомі кути.
5. Катети прямокутного трикутника дорівнюють 21 см і 28 см. Знайти гіпотенузу.

6. Одна із сторін паралелограма на 4 см менша від другої, а периметр його дорівнює 68 см. Знайти сторони паралелограма.

 

7. Знайти довжину медіани ВК трикутника АВС з вершинами А (-3; 3), В (4; 1), С (3; 5).

8. У  рівнобічній  трапеції  більша  основа  10  см,  бічна сторона 4 см, а кут між ними 60°. Знайдіть периметр трапеції.

 

1)  У ромба діагоналі...

2)  Квадрат катета дорівнює ...

3)  Катет, що прилягає до кута а дорівнює ...

8) Обчислити   периметр   рівнобічної   трапеції, якщо відомо, що один з її кутів 60, а основи дорівнюють 17 см і 49 см.