Творча робота «Музей числових диковинок» 8 клас

У світі чисел, як і в світі живих істот, зустрічаються справжні дива, рідкісні екземпляри, що володіють винятковими властивостями. З таких незвичайних чисел можна було б скласти свого роду музей числових рідкостей. У ньому знайшли б собі місце не тільки числові велетні, а й числа скромних розмірів, якi виділяються з ряду інших будь-якими властивостями. Деякі з них вже по зовнішності привертають до себе увагу; інші відкривають свої дивовижні особливості лише при ближчому знайомстві. Ми зробимо екскурсію по галереї таких числових чудасій і познайомимося з деякими з них.

                                                                Число 365

Воно чудово насамперед тим, що визначає число днів в році. Далі, при розподілі на 7 воно дає в залишку 1; ця несуттєва, здавалося б, особливість числа 365 має велике значення для нашого семиденного календаря.

Інша особливість числа 365 не пов'язана з календарем:

365 = 10 * 10 + 11 * 11 + 12 * 12

Тобто 365 дорівнює сумі квадратів трьох послідовних чисел, починаючи з 10:

100 + 121 + 144 = 365.

На цій властивості числа 365 засноване завдання С.А.Рачинського, зображена на відомій картині "Важке завдання" Богдана - Бельського:

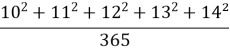
Таких чисел не багато набереться в нашому музеї арифметичних дивинок.

                                     Три дев'ятки 

У наступній вітрині виставлено найбільше з усіх тризначних чисел: 999.

Цікава особливість числа 999 проявляється при множенні на нього всякого іншого тризначного числа. Виходить шестизначне число; перші три цифри його є множимо число, зменшене на одиницю, а інші три цифри - "доповнення" перших до 9, наприклад:

                                                                    573*999=

Варто лише поглянути на наступний рядок, щоб зрозуміти походження цієї особливості:

                                                         573*999=573*(1000-1)=

Знаючи цю особливість, ми можемо "миттєво" множити будь-яке тризначне число на 999.

947 * 999 = 946053

509 * 999 = 508491

981 * 999 = 980019 і т.д.

А так як 999 = 9 * 111 = 3 * 3 * 3 * 27, то ви можете, знову-таки з блискавичною швидкістю, писати цілі колони шестизначних чисел, кратних 37; незнайомий з властивостями числа 999, звичайно, зробити цього не в змозі. Коротше кажучи, ви можете влаштовувати перед необізнаними маленькі сеанси "миттєвого множення і ділення".

                          число Шехеразади

Наступне на черзі у нас число 1001-прославлене число Шехерізади. Ви, ймовірно, і не підозрювали, що в самій назві збірки чарівних арабських казок полягає також свого роду чудо, яке могло б вразити уяву казкового султана не менше багатьох інших чудес Сходу, якби він здатний був цікавитися арифметичними диковинками.

Чим же чудне число 1001? На вигляд воно здається досить звичайним. Воно навіть не належить до обраного розряду так званих "простих" чисел. Воно ділиться без залишку на 7, і на 11, і на 13-на три послідовних простих числа, добутком яких воно і є.

Але не в тому дивина, що число 1001 = 7 * 11 * 13, -тут немає ще нічого чарівного. Бiльш чудне те, що при множенні на нього тризначного числа виходить результат, що складається з самого помноженого числа, тільки написаного двічі, наприклад:

873 * 1001 = 873873

207 * 1001 = 207207 і т.д.

І хоча цього і слід було очікувати, так як 873 * 1001 = 873 * 1000 + 873 = 873000 + 873, -все ж, користуючись зазначеною властивістю "числа Шехерізади", можна досягти результатів зовсім несподіваних, що здаються чарівними, -хоча б, людині непідготовленiй.

Зараз пояснимо, в чому справа.

Товаришів, не посвячених у арифметичні таємниці, ви можете вразити наступним фокусом. Нехай хто-небудь напише на папірці секретно від вас тризначне число, яке хоче, і потім нехай припише до нього ще раз те ж саме число. Вийде шестизначне число. Запропонуйте тому ж товаришеві або його сусідові розділити, таємно від вас, число на 7; при цьому ви заздалегідь передбачаєте, що залишку не вийде . Результат передається новому сусідові, який на вашу пропозицію ділить його на 11; і хоча ви не знаєте числа, ви все ж сміливо стверджуєте, що і воно розділиться без остачі. Отриманий результат ви спрямовуєте наступному сусідові, якого просите розділити це число на 13, - ділення знову виконується без залишку, про що ви заздалегідь попереджуєте. Результат третього поділу ви, не дивлячись на отримане число, вручаєте першому товаришеві зі словами:

 - Ось і число, яке ти задумав!

- Так і є: ти вгадав.

Яка розгадка фокуса?

Цей арифметичний фокус, що виробляє на непосвячених враження чарівництва, пояснюється дуже просто: згадайте, що приписати до тризначного числа його само-значить помножити на 1001, тобто на 7 * 11 * 13. Шестизначне число, яке ваш товариш отримає після того, як припише до задуманого числа його саме, повинно буде тому ділитися без залишку і на 7, і на 11, і на 13; а в результаті поділу послідовно на ці 3 числа воно повинно, звичайно, знову дати задумане число.

                                             Число 10101

Після сказаного про число 1001 вже не буде несподіванкою побачити у вітринах нашого музею число 10101. Ви здогадаєтеся, який саме властивості зобов'язане це число такою честю. Воно, як і число 1001, дає дивовижний результат при множенні, але не тризначних чисел, а двозначних; кожне двозначне число, помножене на 10101, дає в результаті саме себе, написане тричі. Наприклад:

73 * 10101 = 737373,

21 * 10101 = 212121.

Причина усвідомлюється з наступного рядка:

                                            73*10101=73*(10000+100+1)=

Чи можна проробляти з допомогою цього числа фокуси надзвичайного відгадування, як за допомогою числа 1001?

Так можна. Тут можливо навіть обставити фокус різноманітніше, якщо мати на увазі, що 10101 є добутком чотирьох простих чисел:

10101 = 3 * 7 * 13 * 37

Запропонувавши товаришеві задумати якесь двозначне число, ви пропонуєте другому приписати до нього те саме число, а третьому-приписати те саме число ще раз. Четвертого ви просите розділити шестизначне число на 7; п'ятий товариш повинен розділити отримане число на 3; шостий ділить те, що вийшло на 37, і, нарешті, сьомий ділить цей результат на 13, причому всі чотири поділи виконуються без залишку. Результат останнього поділу ви просите передати першому товаришеві: це і є задумане їм число.

При повторенні фокуса ви можете внести в нього деяку різноманітність, звертаючись щоразу до нових дiльникiв. А саме, замість чотирьох множників 3 * 7 * 13 * 37 можете взяти такі групи трьох множників 21 * 13 * 37; 7 * 39 * 37; 3 * 91 * 37; 7 * 13 * 111.

10101, -мабуть, навіть дивніше чарівного числа Шехерізади, хоча і менш відоме своїми вражаючими властивостями. Про нього писалося, втім, ще двісті років тому в "Арифметиці" Магницького, в розділі, де наводяться приклади множення "з подивом".

З тим більшою підставою повинні ми включити його в наше зібрання арифметичних диковинок.

                          Числові піраміди

У наступних вітринах музею нас вражають числові пам'ятки зовсім особливого роду-деяка подоба пірамід, складених з чисел. Розглянемо ближче першу з них:

                                                                        1 * 9 + 2 = 11

                                                                      12 * 9 + 3 = 111

                                                                    123 * 9 + 4 = 1111

                                                                  1234 * 9 + 5 = 11111

                                                                12345 * 9 + 6 = 111111

                                                              123456 * 9 + 7 = 1111111

                                                            1234567 * 9 + 8 = 11111111

                                                          12345678 * 9 + 9 = 111111111

Як пояснити ці своєрідні результати множення?

Щоб осягнути цю дивну закономірність, візьмемо для прикладу якийсь із середніх рядів нашої числової піраміди, наприклад: 123456 * 9 + 7. Замість множення на 9 число можна помножити на (10-1), тобто приписати 0 і відняти множники:

                                                  123456*9+7=1234560+7-123456=

Досить поглянути на останнє віднімання, щоб зрозуміти, чому тут виходить результат, що складається тільки з одних одиниць.

Ми можемо усвідомити собі це, виходячи з інших міркувань. Щоб число виду 12345 ... перетворилося в число виду 11111 ..., потрібно з другої його цифри відняти 1, з третьої 2, з четвертої-3 і т.д-інакше кажучи, відняти від нього те саме число виду 12345 ..., вдесятеро зменшене і попередньо позбавлене останньої цифри. Тепер зрозуміло, що помножити на 10, додати до нього наступну за останньою цифру і відняти від результату початкове число (а помножити на 10 і відняти множиме-значить помножити на 9).

                        Цифровi сходи

Цікаво, що вийде, якщо число 111111111, помножити само на себе? Заздалегідь можна підозрювати, що результат повинен бути дивовижний, але який саме?

Якщо ви володієте здатністю чітко малювати в уяві ряди цифр, вам вдасться знайти цікавий для нас результат, навіть не вдаючись до викладкам на папері. По суті, тут справа зводиться тільки до належного розташуванню добуткiв, тому що множити доводиться весь час лише одиницю на одиницю. Додавання ж добуткiв зводиться до простого рахунку одиниць. Ось результат цього єдиного в своєму роді множення:

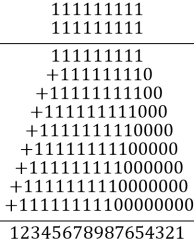
Всі дев'ять цифр симетрично зменшуються від середини в обидві сторони.