"Теорема про три перпендикуляри", розробка уроку

Тема уроку:  "Теорема про при перпендикуляри".

Мета уроку: 

• сформулювати пряму та обернену теореми про три перпендикуляри (ТТП) , навчати через моделювання висувати гіпотези і доводити їх;
•  навчити застосовувати відповідні теореми до розв’язування задач;
• розвивати логічне мислення учнів, виховувати графічну культуру.

Тип уроку:    урок  формування нових знань.

Обладнання: мультимедійна дошка, палички і пластилін, заготовки з кресленням.

Хід уроку

І. Актуалізація опорних знань учнів.

    Інтелектуальна розминка (слайд 3).

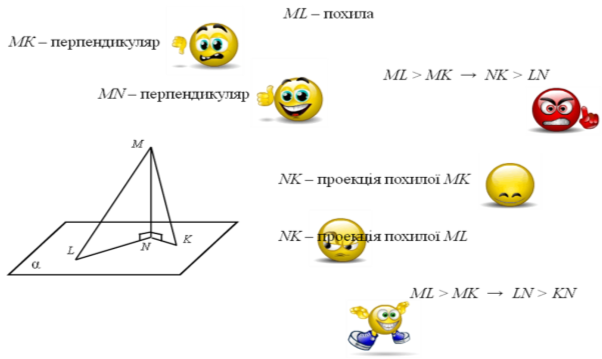
1. Що називається перпендикуляром до площини?

Перпендикуляром, опущеним із даної точки на дану площину, називається відрізок, що сполучає дану точку з точкою площини й лежить на прямій, перпендикулярній до площини.

2. Що називається похилою до площини?

Похилою, проведеною з даної точки до даної площини, називається будь-який відрізок, який сполучає дану точку з точкою площини і не є перпендикуляром до площини.

3. Що називається проекцією похилої?

Відрізок, який сполучає основи перпендикуляра й похилої, проведених з однієї і тієї самої точки, називається проекцією похилої.

4. Сформулювати ознаку перпендикулярності прямої і площини.

Якщо пряма перпендикулярна до двох прямих, які лежать у площині й перетинаються, то вона перпендикулярна до даної площини.

5.  Вказати правильні твердження до відповідних рисунків (слайди 4, 5 створені з використанням тригерів).

ІІ. Вивчення нового матеріалу.

Сьогодні на уроці ми доведемо теорему про три перпендикуляри та  застосовуватимемо  її  при розв'язуванні задач (слайд 6).

Теорема. Якщо пряма, яка проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна і до похилої (пряма теорема).

Якщо пряма на площині, перпендикулярна похилої, то вона перпендикулярна і до її проекції (обернена теорема).

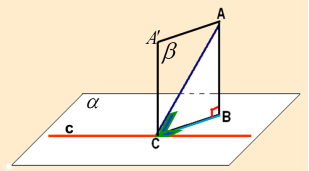 Доведення.

1. Виконаємо додаткову побудову:

проводимо ;

площину через АВ і А₁С.

      .

А тепер, ознайомившись з ТТП,  кожен з учнів за допомогою паличок та пластиліну зробить свою модель до цієї теореми.

ІІІ. Формування умінь та навичок застосовувати ТТП.

• Задачі на побудову (слайд 7,8).

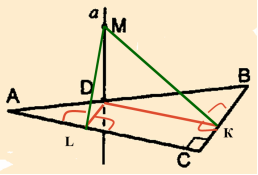
Задача 1. Через гіпотенузу АВ прямокутного трикутника проведено перпендикуляр MD до площини трикутника. Побудуйте перпендикуляри з точки М до катетів трикутника.

Побудова.

Проведемо DK║AC, так як , то (за вл. паралельних прямих). → (за ТТП).

Аналогічно проводимо .   

Задача 2. Побудуйте перпендикуляр з точки М до прямої ВС (слайд 8).

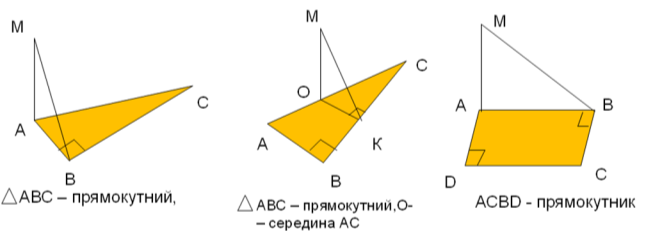
(учні  працюють самостійно: будують обраний малюнок, трьом учням роздано заготовки з рисунками на аркушах А3 і вони ж після побудови виходять з поясненням до дошки).

• Задачі на доведення (слайд 9).

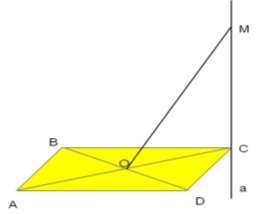
Задача 3. З вершини гострого кута С ромба проведено перпендикуляр МС до площини ромба. Довести, що пряма МО перпендикулярна діагоналі ВD ромба. 

Запитання до розв’язування задачі:

• визначити на малюнку потрібний для доведення задачі перпендикуляр, похилу та пряму на площині;
• сформулювати ознаку діагоналей ромба.

Доведення

Розглянемо – прямокутній.

МО – похила, ОС – проекція похилої, ВD – пряма на площині.

Так, як ОС┴ВD (за властивістю діагоналей ромба) і ОС є проекцією МО на площину АВС, то за ТТП МО ┴ВD.

• Задачі на обчислення (слайд 9-10).

Задача 4. АМ – перпендикуляр проведений до площини рівнобедреного трикутника, дорівнює 4 см, основа трикутника – 8 см, а бічні сторони – 5 см. Знайти відстань від точки А до основи трикутника. 

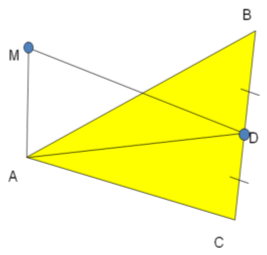І етап – побудова

 Запитання до розв’язування задачі

• що таке відстань від точки до прямої?
• як провести перпендикуляр з точки М до прямої ВС?
• як провести перпендикуляр з точки А до ВС?

Розв’язання

1. Сполучаємо вершину А з серединою D сторони ВС (за властивістю медіани рівнобедреного трикутника). Так, як   проекція   АD ┴ BC,  то   за    ТТП  її похила МD┴BC. Отже, довжина МD є відстанню від точки М до ВС.

ІІ етап – обчислення

• як можна знайти MD?

З прямокутного трикутника АМD. Але в ньому недостатньо даних. Необхідно знайти АD.

• як знайти AD?

Необхідно розглянути планіметричну задачу.

Знайти висоту  АD рівнобедреного трикутника за відомою основою і бічною стороною.

2. З прямокутного ▲АDС: АD = 3 см.

  3. Так, як МА┴(АВС), то МА ┴АD.

  З прямокутного ▲МАD: МD = 5 см.

Відповідь. 5 см.

ІV.  Підсумок уроку.

1. Сформулювати теорему про три перпендикуляри та теорему, обернену до неї.
2. Назвати учнів, які були активні на уроці, виставити оцінки.

5.             Домашнє завдання.

П.148 (довести обернену ТТП),  № 42 (учні роблять модель до домашньої задачі, вказують шляхи її розв’язку).