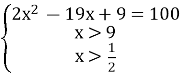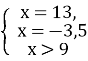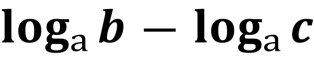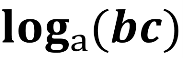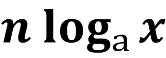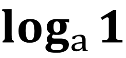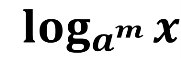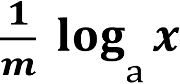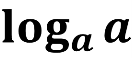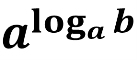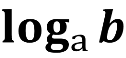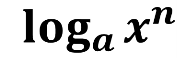Урок "Логарифмічні рівняння"
Тема уроку: Логарифмічні рівняння
Цілі:
- Формування предметних компетентностей: сформувати вміння розв’язувати логарифмічні рівняннярізними способами із використанням властивостей логарифма й логарифмічної функції та зведенням до алгебраїчних рівнянь шляхом заміни змінних;
- Формування ключових компетентностей:
- аргументувати, доводити правильність тверджень;
- прагнути до вдосконалення результатів своєї діяльності;
- генерувати нові ідеї, використовувати критерії раціональності, практичності, ефективності та точності із метою вибору найкращого рішення;
- сприяти самовихованню старанності, охайності, чесності, самокритичності.
Тип уроку: комбінований
Основні терміни і поняття для вивчення: логарифмічне рівняння, потенціювання, властивості логарифма
Обладнання: презентація, картки із завданнями
Форми роботи: індивідуальна, колективна, самостійна робота
Епіграф уроку:
Вчитись можна тільки весело.
Щоб перетравлювати знання,
потрібно поглинати їх з апетитом.
А. Франс.
Конспект уроку
І. Організаційний момент
ІІ. Перевірка домашнього завдання (5 хв)
Знайди помилку товариша
Учні обмінюються зошитами і звіряють д/з свого товариша з виконаними завданнями на слайді і оцінюють свого товариша: правильне виконане завдання – 3 б., 1 помилка – 2 б., 2 помилки – 1 б., 3 і більше помилок – 0 б.
№21.2
-
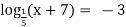 2)
2)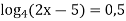
х+7 =![]() ОДЗ: х+7
ОДЗ: х+7![]() 0 2х-5 =
0 2х-5 =![]() ОДЗ: 2х - 5
ОДЗ: 2х - 5![]() 0
0
х+7=![]() х
х![]() -7 2х-5=2 х
-7 2х-5=2 х![]() 2,5
2,5
х+7=125 (-7;![]() ) х=3,5 (2,5;
) х=3,5 (2,5;![]() )
)
х=118
Відповідь: 118 Відповідь: 3,5
![]() -5х -3) = 2 4)
-5х -3) = 2 4) ![]() -5х+6) = -1
-5х+6) = -1
х2- 5х -3 ![]() ОДЗ: х2- 5х -3
ОДЗ: х2- 5х -3![]() 0 х2- 5х +6 =
0 х2- 5х +6 = ![]() ОДЗ: х2- 5х +6
ОДЗ: х2- 5х +6![]() 0
0
х2- 5х -6=0 (х ![]() )
)![]() х2- 5х +4=0 ( х – 3)(х-2)
х2- 5х +4=0 ( х – 3)(х-2) ![]() 0
0
х= -1 х=6 (-![]() )
)![]() (
(![]() ;
;![]() ) х=1 х=4 (-
) х=1 х=4 (-![]() ;2)
;2)![]() (3;
(3;![]()
Відповідь: -1; 6 Відповідь: 1 ; 4
Злови помилку
№21.4
-
log9(4x-6) = log9(x-2) 2)
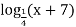 =
= 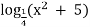
4х – 6 = х – 2 х + 7 = х2 + 5
3х = - 8 х2 – х + 2 = 0
х = 1![]() х = - 2 х =+ 1
х = - 2 х =+ 1
ОДЗ : ![]() ; ОДЗ:
; ОДЗ: ![]() ;
;
![]() ; х
; х![]()
(2;![]() ) ( - 7 ;
) ( - 7 ; ![]() )
)
Відповідь: рівняння коренів не має Відповідь : -1; 2
_________________________________________________________________
1) log9(4x-6) = log9(x-2) 2) ![]() =
= ![]()
4х – 6 = х – 2 х + 7 = х2 + 5
3х = 4 х2 – х - 2 = 0
х = 1![]() х = 2 х = - 1
х = 2 х = - 1
ОДЗ : ![]() ; ОДЗ:
; ОДЗ: ![]() ;
;
![]() ; х
; х![]()
(2;![]() ) ( - 7 ;
) ( - 7 ; ![]() )
)
Відповідь: рівняння коренів не має Відповідь : -1; 2
------------------------------------------------------------------------------------------------------
ІІІ. Мотивація навчальної діяльності школярів, повідомлення теми, мети і завдань уроку (1 хв)
- Я сподіваюся, що цей урок пройде цікаво, з великою користю для всіх. Дуже хочу, щоб ті, хто ще байдужий до цариці всіх наук, з нашого уроку пішов із глибоким переконанням: Математика - цікавий і дуже потрібний предмет.
Алгебру називають теорією розв’язування рівнянь. Сьогодні ми будемо вдосконалювати вміння розв’язувати логарифмічні рівняння. Для успішного розв’язування вправ на уроці ми повинні вміти:
- правильно визначати тип логарифмічних рівнянь;
- застосовувати властивості логарифма;
ІV. Відтворення і корекція опорних знань, навичок і умінь, необхідних учням для самостійного виконання практичного завдання (5 хв)
Хвилинка ерудита (фронтальне опитування)
- Що називають логарифмом числа N за основою a?
Логарифмом числа N основою а називають показник степеня х, до якого треба піднести а, щоб дістати число N.
- Як правильно прочитати запис log216 ?
Логарифм числа 16 за основою 2
- Що означає запис lg N , ln N?
десятковий логарифм- логарифм числа N за основою 10,
натуральний логарифм – логарифм числа N за основою е=2,718…
- Чому дорівнює логарифм числа 1 за основою а?
loga1 = 0
- Чому дорівнює логарифм числа а за основою а?
logaa =1
- Чому дорівнює логарифм добутку?
log a(bc) = logab +logac , b>0, c>0 (логарифм добутку двох додатних множників дорівнює сумі їх логарифмів)
- Чому дорівнює логарифм частки?
loga(![]() ) = logab – logac , b>0, c>0 (логарифм частки двох додатних виразів дорівнює різниці логарифмів діленого і дільника)
) = logab – logac , b>0, c>0 (логарифм частки двох додатних виразів дорівнює різниці логарифмів діленого і дільника)
- Чому дорівнює логарифм степеня?
loga bm = m logab , (логарифм степеня додатного числа дорівнює показнику степеня, помноженому на логарифм основи цього степеня)
- Чи існує логарифм від’ємного числа? ( Ні )
- Основна логарифмічна тотожність.
![]()
![]() . Вивчення нового матеріалу.
. Вивчення нового матеріалу.
Питання: Які рівняння називаються логарифмічними?
Логарифмічними рівняннями називаються рівняння, що містять невідому величину під знаком логарифма або його основі (або в обох місцях одночасно).
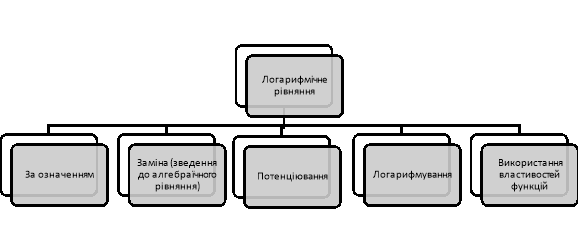
«Навчаючи – вчуся»
На попередньому уроці учні об’єднуються в «домашні» групи і одержують завдання розглянути способи розв’язання логарифмічних рівнянь , скласти алгоритм розв’язання рівняння кожним методом.( 1 група – зведення логарифмів до однієї основи; 2 група – зведення до алгебраїчного шляхом заміни; 3 група – метод потенціювання; 4 група – метод логарифмування.) Представник кожної групи пояснює розв’язання рівняння.
Розв’язати рівняння:
1) ![]() 2) log2 x + logх 2 =
2) log2 x + logх 2 = ![]()
Вказівка: logх 2 = ![]()
3) lg( x2+ 75) = 2 + lg (x-4) 4)хlgx +2 = 1000
Зведення логарифмічного рівняння до однієї основи
Розв’язати рівняння ![]()
|
1. |
Зведемо всі логарифми до основи 2 |
|
|
2. |
Зведемо подібні доданки |
|
|
3. |
Розділимо ліву і праву частини рівняння на |
х=24 х=16 ОДЗ: х>0 |
|
4. |
Запишемо відповідь |
Відповідь: 16 |
Зведення логарифмічних рівнянь до алгебраїчного шляхом заміни
Розв’язати рівняння log 2 2 x+ log2 x3 – 4 = 0
|
1. |
Виконавши тотожні перетворення, звести до логарифмів однієї основи |
log 2 2 x+ 3 log2 x – 4 = 0
|
|
2. |
Виконати заміну |
Заміна: log2 x =t t2 +3t -4 = 0 |
|
3. |
Розв’язати отримане квадратне рівняння відносно нової змінної |
t= - 4 ,t = 1 |
|
4. |
Повернутися до заміни і розв’язати сукупність логарифмічних рівнянь |
log2 x= - 4 log2 x = 1 х=2-4 х=2
х= |
|
5. |
Враховуючи ОДЗ, записати відповідь |
ОДЗ: х
Відповідь : |
Метод потенціювання
Розв’язати рівняння lg(x-9) +lg (2x-1) = 2
|
1. |
Число 2 представимо у вигляді десяткового логарифма |
lg(x-9) +lg (2x-1) = lg100
|
|
2. |
Суму логарифмів замінимо логарифмом добутку виразів |
lg(x-9)(2x-1) = lg100
|
|
3. |
Замінимо рівносильною системою враховуючи ОДЗ: |
|
|
4. |
Відповідь: |
13 |
Метод логарифмування
Розв’язати рівняння ![]()
|
1. |
Знайдемо ОДЗ |
х |
|
2. |
Прологарифмуємо обидві частини рівняння за основою 10, використавши властивість логарифма степеня і частки |
lg2x =2- lg x
|
|
3. |
Розв’яжемо квадратне рівняння відносно lg x |
lg2x+ lg x -2 =0 Заміна: lg x=t t2 + t – 2 =0 t=-2 , t = 1 |
|
4. |
Розв’яжемо сукупність логарифмічних рівнянь |
lg x = - 2 lg x = 1 х = 10-2 х=10 х=0,01 |
|
5. |
Запишемо відповідь: |
0,01 ; 10 |
- lg( x2+ 75) = 2 + lg (x-4)
-
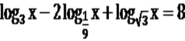
- хlgx +2 = 1000
- log2 x + logх 2 =
Підказка: logх 2 = ![]()
VI. З історичних джерел. Історія виникнення логарифмів і їх застосування
Перші зародки поняття логарифма можна знайти в Архімеда, але сама ідея розвитку не набула. Триста років тому в епоху Відродження почався бурхливий розвиток науки, техніки і мореплавства. Розвиток астрономії, а точніше астрономічних спостережень, вимагали нових методів обчислень, які були б доступні широкому колу людей. В основу таких методів і були покладені логарифми.
_____________________________________________________________________
Перші таблиці логарифмів склав швейцарський механік, годинникар, астроном і математик І.Бюргі (1552-1632). Він довго не наважувався їх опублікувати і лише в 1620 році за наполяганням Кеплера він їх видав. Оригінал цих таблиць зберігається зараз у Пулковській обсерваторії в С.-Петербурзі.
______________________________________________________________________
За свою неквапливість Бюргі поплатився пріоритетом. В 1614 році в Англії шотландський математик Джон Непер, барон, який займався різними науками, особливо астрономією і математикою, надрукував таблиці логарифмів тригонометричних функцій від 0º до 90º. До речі, натуральний логарифм в честь Непера називають Неперовим логарифмом.
Ці таблиці допомагали астрономам і інженерам, скорочуючи час на обчислення, а отже, як сказав знаменитий французький вчений Лаплас, "продовжували життя обчислювачам".
_______________________________________________________
Для обчислення логарифмів довгий час використовували логарифмічну лінійку, яку сконструював англійський математик, священик Оутред в 17 ст. Близько 350 років вона залишалася надійним апаратом для наближених, але швидких обчислень. Але час іде, наука і техніка рухаються вперед, і на зміну логарифмічній лінійці прийшов мікрокалькулятор.
Своє застосування знайшла логарифмічна функція і в астрономії. Наприклад, якщо порівняти характеристики яскравості зірок, то можна побудувати такий графік:

На вертикальній осі відкладаємо яскравість зорі в одиницях Гіппарха ( розподіл зірок по суб’єктивним характеристикам), а по горизонтальній – показання приборів( світність зорі).
За графіком видно, що об’єктивні та суб’єктивні данні не пропорційні, а прибор реєструє зростання блиску в 2 рази. Ця залежність виражається логарифмічною функцією.
__________________________________________________________________
У фізиці також можна знайти багато прикладів застосування логарифмічної функції та логарифмів.
№ 21.9 (1,2) 21.17 (1,2)
VII. Підсумок уроку.
Кросворд
-
Назва
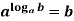
- Логарифм числа – це …
- Один із способів розв’язання логарифмічних рівнянь
- Перша дія під час розв’язання рівняння log2x + log8x=5
- Сума логарифмів двох додатних виразів дорівнює логарифму …
- Перетворення, за допомогою якого за даним логарифмом числа визначають саме число, називається ….
- Логарифм частки двох додатних виразів дорівнює …
VIII. Домашнє завдання. п.21, №21.10(2,3) 21.18(1,2)
Використана література: Алгебра. 11 клас: підручник для загальноосвітніх закладів: академічний рівень, проф.. рівень /А.Г. Мерзляк, Д.А. Номіровський, В.Б. Полонський, М.І. Якір. – Х: Гімназія, 2011. – 431 с. :іл..
|
|
|
|
|
|
|
0 |
|
|
|
|
|
1 |
|
|
b |
|
|
logab +logac |
|
|
|
|


про публікацію авторської розробки
Додати розробку

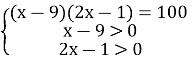 ;
;