Тест. Повторення теми "Тригонометричні рівняння та нерівності"

«На Урок»

Повторення теми "Тригонометричні рівняння та нерівності"

 

1.     Виберіть неправильне твердження:

а)область визначення функції у = arccosX є проміжок [-1; 1];

б)функція у = arctgX додатна, якщо х˃0, і від’емна, якщо х˂0;

в)для всіх х ͼ [0;π] arcsin( sin x) =x;

г)Жодна з обернених тригонометричних функцій не періодична;

д)функція у = arcsin х зростає на всій області визначення

2.

Укажіть, яке з рівнянь не має розв’язків:

а)cos (x + π/4) = - 0,5√3 ; 

б)ctg2x - √3 = 0   

в)sin3x + √3 = 0 

г)ctg√3 x = 2 √3

д)sin(x +√3/4) = - √3/4

3.

З’ясуйте, скільки спільних розв’язків мають рівняння  sinx+1/2=0  і √3tgх-1 = 0 на проміжк (0; 2π)

а)0;  б)1;  в)2;  г)3;  д)безліч.

4.

Виберіть рисунок, на якому зображено множину розв’язків нерівності  cos х˂ - ½:

а)

 

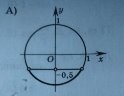
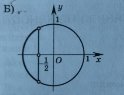
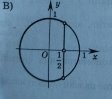
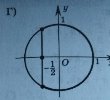
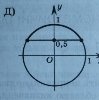
5.

Обчисліть 3sin (arcsin ½ + arcsin(- 1/3) )

а)1,5 - √2;    б)√2 - √3/2;  в)6 - 4√2;   г)4√2 – 6;    д)1,5.

6.

Розв’яжіть нерівність  sin x + √3 cos x ˃ 1

а)(-π/6 +2πk;π/2 + 2πk), kͼ Z;

б)(-π/6 +2πk;π/6 + 2πk), kͼ Z;

в)(π/6 +2πk; 5π/6 + 2πk), kͼ Z; 

г)(π/6 +πk; 5π/6 + πk), kͼ Z;

д)(-π/6 +πk; 7π/6 + πk), kͼ Z.

7.

Знайдіть усі розв’язання рівняння cos² x - sin² x = 1/2

а)±π/6 + πk, kͼZ ;    

б)±π/6 +2 πk, kͼZ ;    

в)(-1)^k π/6 + πk, kͼZ;       

г)(-1)^k+1 π/6 + πk, kͼZ;      

д)(-1)^k+1 π/6 +2 πk, kͼZ.     

8.

Укажіть найменший розв’язок рівняння sin (x – π/4) +√2/2 = 0, якій належить проміжку (-2π: 2π)

а)-π;     б)-π/2;       в)π/2;       г)π;     д)0.

9.

Знайдіть найменший додатний розв’язок рівняння   

sin2x + cos2x = 1/sin2x

а)0;  б)π/8;  в)π/4;  г)π/2;  д)π.

Ключ до тесту

1. в (1 балів)        5. б (2 балів)      

2. в (1 балів)        6. а (2 балів)

3. б (1 балів)        7. а (1 балів)

4. б (1 балів)        8. б (1 балів)     9. б (2 балів)