Тест з теми: "Теорема Фалеса. Подібність трикутників"
Перевірочна робота з геометрії
8 клас (для учнів на сімейному навчанні)
Теорема Фалеса. Подібність трикутників
|
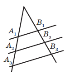
На рисунку А1В1∥ А2 В2, А2В2∥ А3 В3, А1А2=А1А3/2. Звідси випливає, що: А) А1А2=В1В2; В) А1А3=В1В3 ; Б) В1В3=2В2В3 ; Г) А1А2=В2В3.
|
|
- Якщо медіани AA1 і BB1 трикутника ABC перетинаються в точці К, то яка з даних рівностей є правильною для будь-якого трикутника ABC?
А) АК:КВ1=ВК:КА1; В) ![]() ;
;
Б) ![]() ; Г)
; Г) ![]() .
.
|
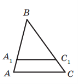
На рисунку А1С1∥ АС. Тоді:
|
|
- У трикутнику ABC відомо, що AB = 8 см, BC = 4 см, AC = 9 см. У якому відношенні центр вписаного кола ділить бісектрису BB1, рахуючи від вершини B?
А) 2 : 3 Б) 4 : 3 В) 2 : 1 Г ) 3 : 4
- Через точку M сторони BC паралелограма ABCD проведено пряму, яка паралельна стороні CD. Ця пряма перетинає відрізки BD і AD у точках K і F відповідно. Відомо, що BM : FD = 2 : 1. Чому дорівнює відношення KD : BK? А) 2 : 1; Б) 1 : 2; В) 1 : 3; Г ) 4 : 1
|
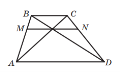
Відрізок MN проведено через точку перетину діагоналей нерівнобедреної трапеції ABCD паралельно її основам. Скільки пар подібних трикутників зображено на рисунку? А) 4; Б) 6; В) 3; Г ) 5 |
|
- У трикутнику ABC відомо, що AB = 14 см, BC = 21 см. На стороні AB на відстані 4 см від вершини A позначено точку D, через яку проведено пряму, паралельну стороні AC. Знайдіть відрізки, на які ця пряма ділить сторону BC.
А) 12 см, 9 см; Б) 15 см, 6 см; В) 18 см, 3 см; Г ) 14 см, 7 см.
- Хорда AB перетинає хорду CD у її середині та ділиться цією точкою на відрізки, які дорівнюють 4 см і 25 см. Знайдіть хорду CD.
А) 10 см; Б) 100 см; В) 5 см; Г ) 20 см.
|
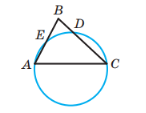
Через вершини A і C нерівнобедреного трикутника ABC проведено коло, яке перетинає сторони BA і BC у точках E і D відповідно. Яка з даних рівностей є правильною
|
|
- У трикутнику ABC відомо, що AB = 10 см, BC = 4 см, CA = 8 см. На стороні AC позначено точку D таку, що AD = 6 см. Знайдіть відрізок BD. А) 5 см; Б) 4 см; В) 6 см; Г ) 7 см


про публікацію авторської розробки
Додати розробку