Тести з теми "Комплексні числа"
Теоретично-практичні тести можуть бути використані учителями математики на різних етапах уроків для проведення занять з алгебри у класах з поглибленим вивченням предмета.
Тематичні тести «Комплексні числа»
Тема 1. «Поняття комплексного числа»
1. Яким є число ![]() ?
?
а) дробовим; б) раціональним; в) комплексним; г) ірраціональним;
д) дійсним.
-
Скільки розв’язків має рівняння
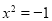 в множині комплексних чисел?
в множині комплексних чисел?
а) один; б) безліч; в) жодного; г) два; д) три.
-
Чому дорівнює
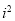 ?
?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
-
Число виду
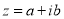 , де
, де 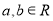 називається:
називається:
а) дійсним; б) раціональним; в) комплексним; г) уявним;
д) ірраціональним.
5. Комплексне число складається з:
а) дійсної та раціональної частини; б) раціональної та уявної частини;
в) цілої та дробової частини; г) дійсної та уявної частини.
6. Дійсною частиною числа ![]() є:
є:
а) ![]() ; б)
; б) ![]() ; в) немає; г)
; в) немає; г) ![]() ; д)
; д) ![]()
-
Назвіть уявну частину числа
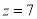 .
.
а) немає; б) 7; в) безліч; г) ![]() ; д)
; д) ![]()
-
Яким вважається комплексне число у випадку
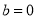 ?
?
а) співпадає з комплексним; б) співпадає з дійсним;
в) чисто уявним; г)нульовим; д) цілим
-
Яким вважається комплексне число у випадку
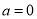 ?
?
а) співпадає з комплексним; б) співпадає з дійсним; в) чисто уявним;
г) нульовим; д) цілим.
-
Як називається число
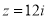 ?
?
а) комплексним; б) дійсним; в) чисто уявним; г) спряженим;
д) цілим.
11. Два комплексні числа ![]() і
і ![]() є рівними при:
є рівними при:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]()
12. Якими вважаються комплексні числа ![]() і
і ![]() , коли
, коли ![]()
а) спряженими; б) рівними; в) додатними; г) чисто уявними;
д) софістичними.
13. Яку назву мають комплексні числа ![]() та
та ![]() :
:
а) рівні; б) спряжені; в) додатні; г) протилежні; д) дробові.
14. Як називаються комплексні числа виду ![]() та
та ![]() ?
?
а) спряженими; б) рівними; в) додатними; г) чисто уявними;
д) софістичними.
15. Коли комплексне число ![]() спряжене з числом
спряжене з числом ![]() ?
?
а) завжди; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д) ніколи.
; д) ніколи.
16. Яким символом позначається комплексне число спряжене до ![]() ?
?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
17. Спряженим до числа ![]() є:
є:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ;
;
18.Спряженим до числа ![]() є:
є:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д) немає.
; д) немає.
19. Чи можна сказати, що одне комплексне число більше від іншого?
а) так; б) ні.
20. Яке з двох комплексних чисел більше ![]() чи
чи ![]() ?
?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) відношення більше не існує; д) ![]() .
.
Тема 2. «Дії над комплексними числами та геометрична інтерпретація комплексних чисел»
-
Сумою двох комплексних чисел
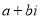 і
і 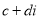 є:
є:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
- Нейтральний елемент по множенню в множині комплексних чисел – це:
а) ![]() ; б)
; б) ![]() ; в) не існує; г)
; в) не існує; г) ![]() ; д)
; д) ![]() .
.
-
Комплексні числа
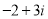 та
та 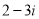 називаються:
називаються:
а) спряжені; б) протилежні; в) рівні; г) невід’ємні; д) дробові.
-
Комплексні числа
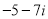 та
та 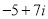 є:
є:
а) спряжені; б) протилежні; в) рівні; г) невід’ємні; д) дробові.
- Означення суми комплексних чисел поширюється на:
а) два доданки; б) три доданки; в) тридцять доданків;
г) від трьох до п’яти доданків; д) безліч доданків.
-
Сума
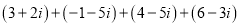 дорівнює:
дорівнює:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
-
Різницею двох комплексних чисел
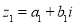 і
і 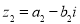 називається число
називається число 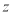 , що задовольняє рівності:
, що задовольняє рівності:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
-
Різницею чисел
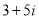 та
та 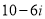 є:
є:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
-
Комплексне число
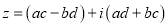 при
при 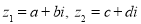
називається:
а) добутком ![]() і
і ![]() ; б) різницею
; б) різницею ![]() і
і ![]() ; в) сумою
; в) сумою ![]() і
і ![]() ;
;
г) часткою ![]() і
і ![]() ; д) піднесення
; д) піднесення ![]() до степеня
до степеня ![]() .
.
-
Яка дія відбувається за правилом
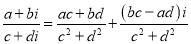 :
:
а) додавання; б) віднімання; в) піднесення до степеня; г) ділення;
д) логарифмування.
- Для того, щоб поділити два комплексні числа необхідно:
а) помножити ділене на число спряжене до дільника;
б) помножити дільник на число спряжене до дільника;
в) помножити ділене і дільник на число спряжене до дільника;
г) помножити ділене на число спряжене до діленого;
д) помножити дільник на число спряжене до діленого.
-
При множенні комплексних чисел
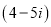 на
на 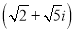 отримаємо:
отримаємо:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() .
.
13. Добуток двох спряжених чисел ![]() і
і ![]() дорівнює:
дорівнює:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
-
Добуток двох комплексних чисел
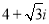 і
і 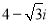 дорівнює:
дорівнює:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
-
Частка двох комплексних чисел
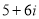 та
та 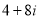 дорівнює:
дорівнює:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
-
Піднести до степеня двочлен
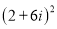 :
:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
- Площина, точки якої зображають комплексні числа називається:
а) декартовою; б) полярною; в) комплексною; г) циліндричною;
д) плоскою.
-
Вісь
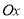 на цій площині називається:
на цій площині називається:
а) абсцис; б) уявна; в) дійсна; г) ординат.
-
Вісь
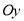 на цій площині називається:
на цій площині називається:
а) абсцис; б) уявна; в) дійсна; г) ординат.
Тема 3. «Тригонометрична форма комплексного числа»
-
Запис комплексного числа
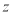 у вигляді
у вигляді 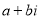 називається:
називається:
а) тригонометричною формою; б) алгебраїчною формою;
в) показниковою формою; г) тригонометричною формою;
д) квадратичною формою.
- Геометричним зображенням комплексного числа є:
а) відрізок; б) пряма; в) радіус-вектор; г) промінь; д) модуль.
-
Величина, що обчислюється за формулою
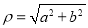 називається:
називається:
а) радіус; б) відрізок; в) модуль; г) промінь; д) радіус-вектор.
-
Число
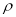 перетворюється в нуль за умов:
перетворюється в нуль за умов:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]()
-
Форма комплексного числа
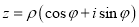 називається:
називається:
а) алгебраїчною; б) показниковою; в) логарифмічною;
г) тригонометричною; д) лінійною.
-
Модуль комплексного числа
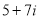 дорівнює:
дорівнює:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
-
Радіус-вектор, що відповідає комплексному числу
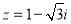 належить:
належить:
а) ![]() чверті; б)
чверті; б) ![]() чверті; в)
чверті; в) ![]() чверті; г)
чверті; г) ![]() чверті;
чверті;
- Для переходу до алгебраїчної форми комплексного числа застосовують
формули:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]()
![]() ; г)
; г) ![]() .
.
-
Визначити дійсну та уявну частини комплексного числа
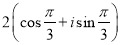 :
:
а) ![]() і
і ![]() ; б)
; б) ![]() і
і ![]() ; в)
; в) ![]() і
і ![]() ; г)
; г) ![]() і
і ![]() ; д)
; д) ![]() і
і ![]() .
.
- Для того, щоб помножити два комплексні числа в тригонометричній
формі необхідно
а) модулі перемножити, а аргументи додати;
б) модулі розділити, а аргументи відняти;
в) модулі розділити, а аргументи додати;
г) модулі перемножити, а аргументи відняти;
- Два комплексні числа рівні в тригонометричній формі, коли
а) рівні їх модулі;
б) рівні їх модулі, а аргументи відрізняються на число кратне ![]() ;
;
в) рівні їх модулі, а аргументи відрізняються на число кратне ![]() ;
;
г) рівні їх аргументи.
Тема 4. «Добування кореня ![]() го степеня з комплексного числа»
го степеня з комплексного числа»
-
Коренем
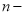 го степеня
го степеня 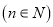 з комплексного числа
з комплексного числа 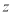 називається:
називається:
а) будь-яке комплексне число, ![]() й степінь якого дорівнює
й степінь якого дорівнює ![]() .;
.;
б) будь-яке комплексне число, ![]() й степінь якого дорівнює
й степінь якого дорівнює ![]() .;
.;
в) будь-яке комплексне число, ![]() й степінь якого дорівнює
й степінь якого дорівнює ![]() .;
.;
г) будь-яке комплексне число;
-
Скільки різних значень кореня
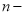 го степеня має комплексне число?
го степеня має комплексне число?
а) ![]() ; б)
; б) ![]() ; в) менше ніж
; в) менше ніж ![]() ; г) більше за
; г) більше за ![]() ; д) кратне
; д) кратне![]() .
.
3. Два комплексні числа рівні в тригонометричній формі, коли рівні їх модулі, а аргументи відрізняються на число кратне
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
4. Число ![]() в тригонометричній формі записується:
в тригонометричній формі записується:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) немає правильної відповіді.
-
Яким чином розташовані корені із
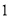 на координатній площині?
на координатній площині?
а) симетрично відносно початку координат;
б) немає правильної відповіді;
в) попарно симетрично відносно уявної осі;
г) симетрично відносно дійсної осі.
- Корінь четвертого степеня із 1 має:
а) 2 значення; б) 8 значень; в) 4 значення; г) безліч значень;
д) ![]() значень.
значень.
-
Для будь-якого цілого числа
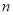 справедлива рівність
справедлива рівність
![]() , яка називається
, яка називається
а) піднесення комплексного числа до степеня; б) формула Бернуллі;
в) формула Ейлера; г) формула Муавра;
д) тригонометрична форма комплексного числа.
Підсумковий теоретично-практичний тест
1. Комплексним числом називається число виду_________________________
__________________________________________________________________
2. Що є дійсною та уявною частинами комплексного числа?_______________
__________________________________________________________________
3. Якою буквою позначають множину всіх комплексних чисел?
__________________________________________________________________
4. Сумою комплексних чисел ![]() та
та ![]() є число______________
є число______________
__________________________________________________________________
5. Запишіть закони додавання комплексних чисел. Доведіть один з них
____________________________________________________________________________________________________________________________________
6. Різницею двох комплексних чисел ![]() та
та ![]() є
є
число_____________________________________________________________
7. Порахувати суму комплексних чисел ![]() та
та ![]() _______________
_______________
__________________________________________________________________
8. Порахувати різницю комплексних чисел ![]() та
та ![]()
__________________________________________________________________
9. Добутком комплексних чисел ![]() та
та ![]() називається число_______________________________________________________________________________________________________________________________
називається число_______________________________________________________________________________________________________________________________
10. Запишіть закони множення комплексних чисел_______________________
____________________________________________________________________________________________________________________________________
11. Перемножити комплексні числа ![]() та
та ![]() __________________
__________________
__________________________________________________________________
12. Розкласти на комплексні множники ![]() __________________________
__________________________
__________________________________________________________________
13. Часткою комплексних чисел ![]() та
та ![]() називається таке комплексне число_______________________________________________________________________________________________________________________________
називається таке комплексне число_______________________________________________________________________________________________________________________________
14. Доведіть, що частка комплексних чисел ![]() та
та ![]() визначена однозначно________________________________________________________
визначена однозначно________________________________________________________
____________________________________________________________________________________________________________________________________
15. Знайти частку комплексних чисел ![]() та
та ![]() _______________
_______________
____________________________________________________________________________________________________________________________________
16. Необхідна і достатня умова, щоб добуток і сума двох комплексних чисел були дійсними числами______________________________________________
__________________________________________________________________
17. Піднести до степеня двочлен ![]() ________________________________
________________________________
__________________________________________________________________
18. Встановіть взаємно однозначну відповідність між множиною комплексних чисел і множиною точок координатної площини__________________________________________________________
____________________________________________________________________________________________________________________________________
19. Площину, точки якої зображають комплексні числа, називають
__________________________________________________________________початок координат якому відповідає число 0 називають___________________
__________________________________________________________________
вісь абсцис називають_______________________________________________
вісь ординат називають______________________________________________
20. Чи можливо геометрично зобразити додавання комплексних чисел? За яким правилом?____________________________________________________
__________________________________________________________________
21. Чи вірно, що ![]() ? Відповідь обґрунтуйте____________________
? Відповідь обґрунтуйте____________________
____________________________________________________________________________________________________________________________________
22. Знайти геометричне зображення суми ![]() комплексних чисел
комплексних чисел ![]() та
та ![]() ________________________________________________________
________________________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
23. Довжина радіус-вектора ![]() називається______________________
називається______________________
__________________________________________________________________
число ![]() дорівнює нулю, якщо________________________________________
дорівнює нулю, якщо________________________________________
__________________________________________________________________
24. Що називається аргументом комплексного числа?____________________
____________________________________________________________________________________________________________________________________
25. Запишіть тригонометричну форму комплексного числа________________
__________________________________________________________________
26. Знайти модуль комплексного числа ![]() ____________________________
____________________________
__________________________________________________________________
27. Чи представлено число ![]() в тригонометричній формі? Якщо ні, то представте це число в тригонометричній формі_____________________
в тригонометричній формі? Якщо ні, то представте це число в тригонометричній формі_____________________
____________________________________________________________________________________________________________________________________
28. Записати комплексне число ![]() в алгебраїчній формі
в алгебраїчній формі
______________________________________________________________________________________________________________________________________________________________________________________________________
29. Записати комплексне число ![]() в тригонометричній формі
в тригонометричній формі
____________________________________________________________________________________________________________________________________
30. Для того, щоб помножити два комплексні числа в тригонометричній формі необхідно______________________________________________________
__________________________________________________________________
31. Для того, щоб розділити два комплексні числа в тригонометричній формі необхідно__________________________________________________________
__________________________________________________________________
32. Знайти частку та добуток двох комплексних чисел ![]() ,
, ![]() ____________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________
33. Коренем ![]() го степеня
го степеня ![]() з комплексного числа
з комплексного числа ![]() називається
називається
__________________________________________________________________
34. Обчислити: ![]() _________________________________________________
_________________________________________________
____________________________________________________________________________________________________________________________________
35. Що утворює множина коренів ![]() го степеня з 1?_____________________
го степеня з 1?_____________________
__________________________________________________________________
36. Записати формули для добування кореня ![]() го степеня з
го степеня з ![]() _____________
_____________
__________________________________________________________________
37. Корінь ![]() го степеня з 1 називається первісним_______________________
го степеня з 1 називається первісним_______________________
__________________________________________________________________


про публікацію авторської розробки
Додати розробку
