Самостійна робота за курс старшої школи у форматі ЗНО
Самостійна робота з алгебри, яка може бути проведена як річна контрольна робота складена у форматі ЗНО. Тестові завдання з варіантом однієї правильної відповіді, завдання на відповідність (кожна відповідність по 1б), завдання з варіантом короткої відповіді по 2б. Максимальна кількість балів 16. Надана шкала переводу балів в 12-б оцінку
Самостійна робота «Повторення за курс старшої школи»
Варіант 1
№1. Обчислити: 
№2. Розв’язати рівняння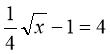 
№3. Знати загальний вигляд первісної: f(x)=cos x – x2
№4. Знайти медіану вибірки: 6; 4; 9; 8; 4; 9; 4; 5; 8.
№5. Розв’язати нерівність: 
№6. Тіло рухається прямолінійно за законом s(t)= 2t2- 5t. Знайти швидкість тіла в момент часу t=3с.
№7. Установіть відповідність між функціями, заданими формулами, та їх властивостями
|
1 |
|
A |
Областю визначення функції є проміжок (-∞;+∞) |
|
2 |
y= cos x |
Б |
Множиною значень функції є проміжок [0;+∞) |
|
3 |
y= |
В |
Функція спадає на проміжку (0;+∞) |
|
4 |
y=arcsin x |
Г |
Періодична функція з найменшим додатним періодом Т=π |
|
|
|
Д |
Непарна функція |
№8 Обчислити sinα, якщо 
№9. Знайти МАКСИМУМ функції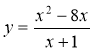 
№10. Розв’язати рівняння: 
. Якщо рівняння має 1 корінь – запишіть його у відповідь, якщо кілька, то у відповідь запишіть його суму.
Оцінювання:
№1-6 по 1б = 6б
№7 по 1б = 4б
№8-10 – по 2б = 6б
Всього 16б
|
Бали |
1 |
2 |
3 |
4 |
5 |
6,7 |
8,9 |
10,11 |
12,13 |
14 |
15 |
16 |
|
Оцінка |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Самостійна робота «Повторення за курс старшої школи»
Варіант 2
№1. Обчислити: 9sinx=10
№2. Розв’язати рівняння 
№3. Знати похідну : f(x)=9cos 
x
№4. У скриньці 5 білих, 2 зелених, 8 жовтих кульок. Навмання беруть одну із них. Яка ймовірність того, що вона буде НЕ БІЛА?
№5. Розв’язати нерівність: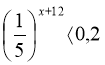 
№6. Знайдіть кутовий коефіцієнт дотичної до графіка функції f(x)=e-
у точці х0= - 1.
№7. Установіть відповідність між рівнянням та твердженнями, що є правильними для цих рівнянь
|
1 |
|
A |
Рівняння не має коренів |
|
2 |
|
Б |
Коренем рівняння є число 2 |
|
3 |
|
В |
Коренем рівняння є від’ємне число |
|
4 |
2 |
Г |
Рівняння має два корені |
|
|
|
Д |
Корінь рівняння належить проміжку (1;2) |
№8 Обчислити площу фігури, обмеженої лініями у=х2-2, у=х
№9. Розв’язати рівняння: 
. У відповідь запишіть кількість коренів рівняння, які належать проміжку [-2π;2π]
№10. Розв’язати нерівність: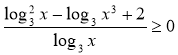 
. У відповідь записати СУМУ ЦІЛИХ розв’язків нерівності, які належать проміжку [-10;+10].
Оцінювання:
№1-6 по 1б = 6б
№7 по 1б = 4б
№8-10 – по 2б = 6б
Всього 16б
|
Бали |
1 |
2 |
3 |
4 |
5 |
6,7 |
8,9 |
10,11 |
12,13 |
14 |
15 |
16 |
|
Оцінка |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
про публікацію авторської розробки
Додати розробку