Схема нарахування балів за виконання завдань контрольної роботи: 

1.    Завдання з вибором однієї правильної відповіді оцінюють у 0 або 1 бал: 1 бал, якщо вказано правильну відповідь; 0 балів, якщо вказано неправильну відповідь, або відповіді на завдання не надано.

2.    Завдання на встановлення відповідності («логічні пари») оцінюють у 1 бал за кожну правильно встановлену відповідність («логічну пару»); 0 балів за будь-яку «логічну пару», якщо зроблено більше однієї позначки в рядку. 

3.    Завдання відкритої форми з короткою відповіддю оцінюють у 0 або 2

бали: 2 бали, якщо вказано правильну відповідь; 0 балів, якщо вказано неправильну відповідь, або відповіді на завдання не надано. 

4.    Завдання відкритої форми з розгорнутою відповіддю оцінюють у 0, 1, 2, або 3 бали. Максимальну кількість балів учень отримує якщо навів усі етапи розв’язання й обґрунтував їх, зробив посилання на математичні факти, з яких випливає те чи інше твердження, проілюстрував розв’язання задачі рисунками, графіками тощо.

Таблиця відповідності тестових балів оцінкам 

Тема: Функції, їх властивості та графіки

Завдання 1-6 мають по п’ять варіантів відповідей, серед яких тільки ОДИН 

правильний. Виберіть  правильну, на вашу думку, відповідь та позначте її в бланку відповідей.

1.   Функція задана формулою f (x)  ₂ . Тоді f (4) дорівнює: x 1

2.   Областю визначення функції f (x)  510x є:

6.        Для побудови графіка функції у=(х+1)³, необхідно виконати:

Завдання 7 передбачає встановлення відповідностей. До кожного рядка, позначеного ЦИФРОЮ доберіть один рядок, позначений БУКВОЮ.

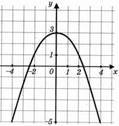
7.        Встановіть за графіком функції її основні властивості.

1.     Функція зростає на:       А. (-2; 4)

2.     Функція спадає на:        Б. (-2; 6)

3.     f(x)>0 на:    В. (1; 6)

4.     f(x)<0 на:   Г. (-2; 1) (6; 9)

                                                                        Д. (4; 9)

Розв’яжіть завдання 8 і 9( з короткою відповіддю). 

 Відповіді  запишіть  у бланку відповідей, дотримуючись правил запису.

8.        Знайдіть точки перетину графіків функцій у = х² і у = 5 – 4х. У відповідь запишіть суму абсцис точок перетину графіків функцій. 

9.        Знайдіть суму натуральних чисел, що входять до області визначення функції

32хх² у х2 .

Наведіть повне розв’язання завдання 10. 

Відповідь  та повне розв’язання запишіть у бланку відповідей. 

10.   Для функції уx²  5x 4

1.     побудувати графік функції;

2.     знайти область значень функції.

Варіант ІІ

Завдання 1-6 мають по п’ять варіантів відповідей, серед яких тільки ОДИН 

правильний. Виберіть  правильну, на вашу думку, відповідь та позначте її в бланку відповідей. x2

1.   Функція задана формулою f (x) . Тоді f (9) дорівнює: x 1

2.   Областю визначення функції f (x)  10 20x є:

4.       Серед наведених графіків зазначте графік функції у 2 х .

5.       Парною є функція:

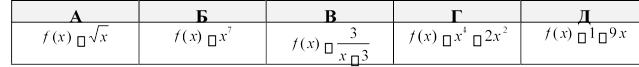
6.       Для побудови графіка функції у=2х² необхідно виконати:

Завдання 7 передбачає встановлення відповідностей. До кожного рядка, позначеного ЦИФРОЮ доберіть один рядок, позначений БУКВОЮ.

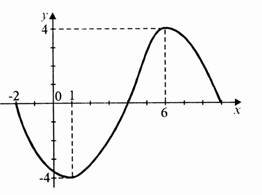
7.       Встановіть за графіком функції її основні властивості.

1.   Функція зростає на:                                А. (-6; 3)

2.   Функція спадає на:                                  Б. (-2; 3)

3.   f(x)>0 на:                                                  В. (-4; 1)

4.   f(x)<0 на:                                                  Г. (-6; - 4) (1; 3)

                                                                      Д. (-6; -2)

Розв’яжіть завдання 8 і 9( з короткою відповіддю). 

 Відповіді  запишіть  у бланку відповідей, дотримуючись правил запису.

8.       Знайдіть точки перетину графіків функцій у = - х² і у = 2х - 15. У відповідь запишіть добуток абсцис точок перетину графіків функцій.

9.       Запишіть кількість цілих розв’язків, які входять до області визначення функції у 

Наведіть повне розв’язання завдання 10.

 Відповідь  та повне розв’язання запишіть у бланку відповідей. 

10.   Для функції𝑦 = |𝑥² − 4𝑥| + 3 1) побудувати графік функції;

2) знайти область значень функції.