Розв’язування задач прикладного характеру.

Тема уроку.Розв’язування задач прикладного характеру.

Мета: формувати уміння і навички учнів застосувати найбільше та найменше значення функції до розв’язування задач прикладного характеру.

Тип уроку: Урок формування вмінь і навичок.

    Хід уроку

1. Актуалізація опорних знань.

Застосовується інтерактивна технологія «Мікрофон». Фронтальне опитування теоретичного матеріалу відбувається у форматі прес-конференції. Два учні, експерти з теми «Застосування похідної до дослідження функції», дають  відповідь на запитання, які підготували учні-кореспонденти.

   Запитання

1. Що таке стаціонарні точки?
2. Сформулюйте необхідну умову існування екстремуму.
3. Сформулюйте достатню умову монотонності функції.
4. Сформулюйте достатню умову екстремуму функції.
5. Як знаходити проміжки монотонності функції?
6. Які етапи знаходження екстремумів функції?
7. Як знаходити найбільше та найменше значення функції на відрізку?

2. Мотивація навчання.

Проблема. Скільки коренів має рівняння

Для розв’язування цього завдання використовується інтерактивна технологія колективного обговорення «Мозковий штурм».

Учні вносять пропозиції щодо розв’язування даного рівняння.

1. Скористатися теоремою про корінь: якщо функція ƒ зростає (спадає)на проміжку I, число а-будь-яке із значень, яких набуває ƒ на цьому проміжку, то рівняння ƒ(х)=а має єдиний корінь на проміжку I.
2. Розглянути функцію ƒ(х)= 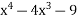та дослідити її на монотонність.

Розв’язання

Розглянемо функцію ƒ(х)=.  D (ƒ)=R.

Знайдемо похідну функції:

 Ƒ’(х)=

Знайдемо критичні точки:

 Ƒ’(x)=0

              X=0 або х=3

На проміжку (-∞;0) функція спадає від +∞ до -9, на цьому проміжку рівняння ƒ(х)=0 має один корінь; на проміжку (0;3) функція спадає від -9до -36, тому рівняння не має коренів; на проміжку (3;+∞) функція зростає від -36 до +∞, а отже, рівняння має один корінь. Тому рівняння має два корені.

Відповідь. 2 корені.

3. Формування умінь та навичок.

Відбувається у формі гри «Просимо розшукати». Роздаються ролі для участі у гру (за бажанням). У грі беруть участь «оперативник», «слідчий», «суддя», «прокурор», «адвокат».

Учитель.  У чергового по відділенню продзвенів телефон. Схвильований голос просив серед усіх прямокутників, площа яких дорівнює , знайти прямокутник з найменшим периметром. Відкрито справу. До справи заучені оперативник та слідчі прокуратури.

Оперативник. Працюючи над справлю, ми висунули версію, що потрібно шукати периметр прямокутника за формулою P=2(a+b). Інтуїція підказує, о найменший периметр має квадрат, але не вистачає доказів (даних) для знаходження периметра.

Слідчий. Проведемо слідчий експеримент

. Нехай х см – ширина прямокутника , а см – довжина прямокутника , тоді

P(x) =2() =

Оскільки Р(х) є функцією від х, то знайдемо значення х, якому відповідає найменше значення Р. Запишемо область визначення функції

P(x) =: D(y) = (0;+∞).

Знайдемо похідну:

P’(x) = 0,

Версію, що х=-3, відкидаємо, бо х>0. Перевіримо, що коли 0<x<3, то P’(x)<0; а коли x>3, P’(x) >0, тобто x=3 – точка мінімуму. Тоді 9:3=3(см).

Слідчий експеримент показав, що з усіх прямокутників з площею 9 стороною 3 см матиме найменший периметр.

Учитель. Слідчо-оперативні служби розслідування завершили і справа передається до суду.

Суддя. Заслуховуємо прокурора та адвоката.

Прокурор. Ознайомившись із справою, я вважаю, що доказів недостатньо для того, щоб стверджувати, що серед прямокутників з площею 9 квадрат зі стороною 3 см має найменший периметр.

Адвокат. Я надаю суду докази того, що з усіх прямокутників з площею 9 квадрат зі стороною 3 см має найменший периметр.  Скориставшись матеріалами слідчого експерименту, знайдемо найменше значення функції. P(x) = на проміжку (0;9].

Знайдемо похідну функції та критичні точки:

P’(x) = +2

P’(x) = 0,

X=-3не входить у даний проміжок. Знайдемо значення периметра:

P (3) = 18:3+2*3=12(см).

P (9) = 18:9+2*9=20(см).

= P (3) = 12.

Суддя. Суд вирішив, що серед прямокутників з площею 9 квадрат зі стороною 3 см справді має найменший периметр.

4. Підсумок уроку.

Учні колективно складають схему розв’язування прикладних задач.

1. Задачу «переводять» на мову функцій. Для цього вибирають зручний параметр х, через який виражають величину, що нас цікавить, як функцію y = ƒ(x).
2. Засобами аналізу знаходять найбільше або найменше значення цієї функції на деякому відрізку або розв’язують задачу на знаходження екстремуму функції.
3. З’ясовують, який практичний зміст  має знайдений результат.

5. Домашнє завдання. 

А.Г. Мерзляк Алгебра 11 клас профільний рівень. №13.23., 13.28.