«tgx = а Основну частину присутніх тут формул Ви повинні вміти легко застосовувати на практичних, а для цього частину матеріалу потрібно завчити та знати.
Про матеріал
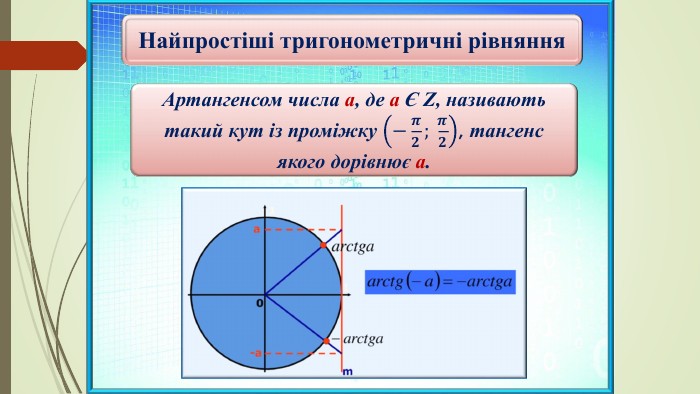
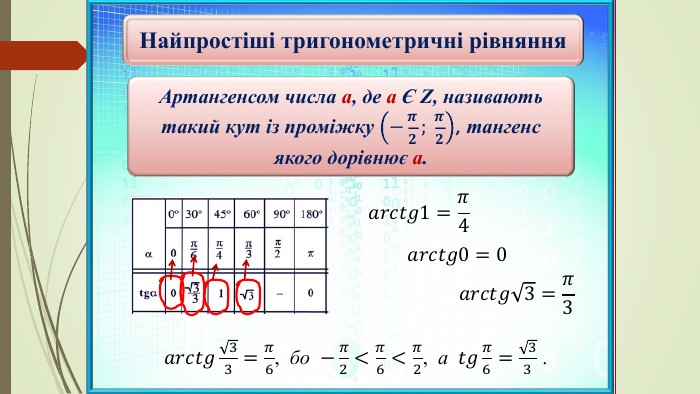
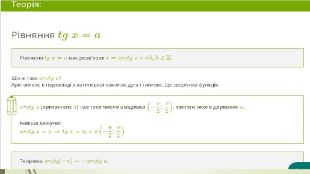
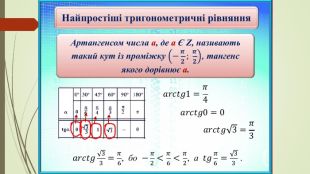
Найпростіші тригонометричні рівняння виду
tg x = a
Наведені та структуровані основні характеристики тригонометричних функцій sin(x), cos(x), tg(x), ctg(x), які є вкрай необхідними при дослідженні графіків та поведінки цих функцій, спрощенні тригонометричних виразів, обчисленні рівнянь та нерівностей.
Основну частину присутніх тут формул Ви повинні вміти легко застосовувати на практичних, а для цього частину матеріалу потрібно завчити та знати.
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку