Трапеція. Розв'язування задач.
Про матеріал
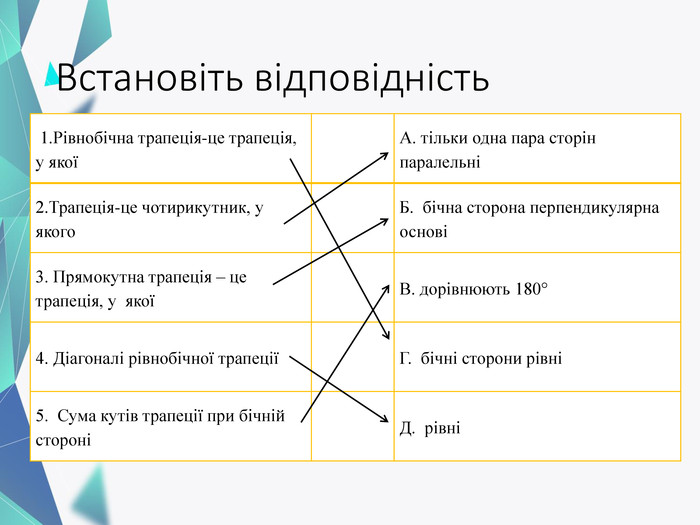
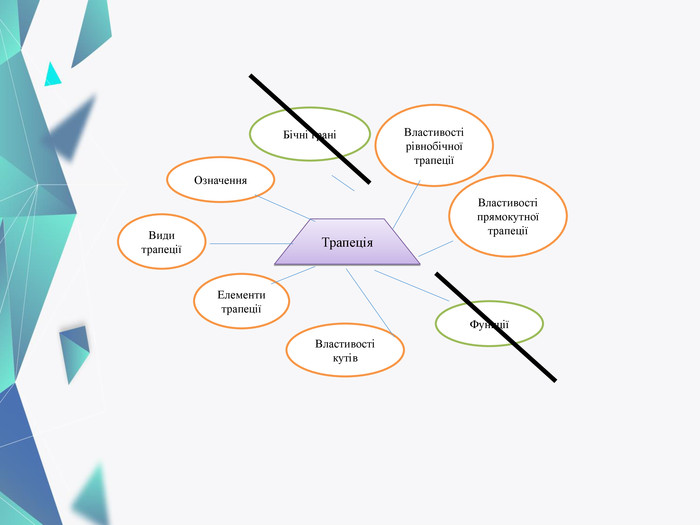
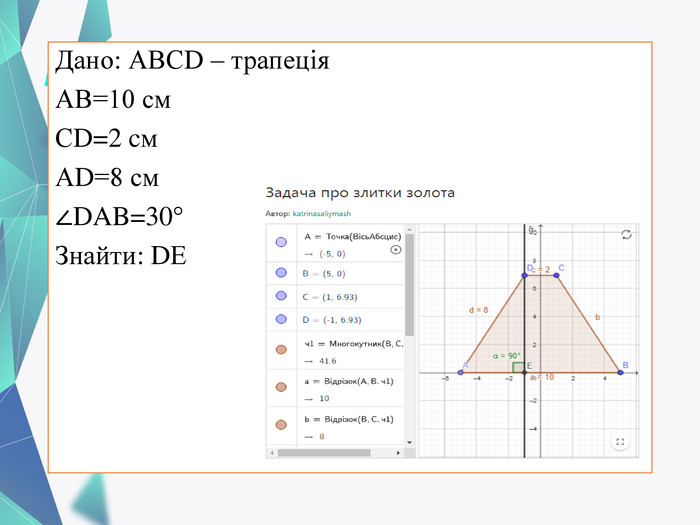
Презентація до уроку "Трапеція. Розв'язування задач", в якій дібрано підбірки задач для формування ключових компетентностей. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку