Творча робота з математики "Прості числа. Сафарі впродовж 2323 роки"

Про матеріал

Матеріали до теми пості числа, які познайомлять учнів зі світом чисел, їх використанням та знаходженням. А також відкриють двері до "Теорії чисел", як розділу математики, відкривши нерозв'язані питання їх досліджень.

Перегляд файлу

Тема творчої роботи з математики

ПРОСТІ ЧИСЛА. САФАРІ ВПРОДОВЖ 2323

Роботу виконала:

Близнюк Марія Олександрівна,

учениця 6 класу

Кропивнянської гімназії

Талалаївської сільської ради

Ніжинського району

Чернігівської області

Учитель:

Градобик Оксана Анатоліївна,

учитель математики

Кропивнянської гімназії

Талалаївської сільської ради

Ніжинського району

Чернігівської області

ЗМІСТ

ВСТУП

РОЗДІЛ І. НАТУРАЛЬНИЙ РЯД ЧИСЕЛ. ДЕ ЖИВУТЬ ПРОСТІ ЧИСЛА.

РОЗДІЛ ІІ. «РЕШЕТО ЕРАТОСФЕНА», «СКАТЕРТИНА УЛАМА»

2.1 Пактична частина. Завдання 1

2.2. Пактична частина. Завдання 2

РОЗДІЛ ІІІ. ВИКОРИСТАННЯ ПРОСТИХ ЧИСЕЛ. ВІДКРИТІ ПИТАННЯ У ВИВЧЕННІ ПРОСТИХ ЧИСЕЛ

РОЗДІЛ ІV. САФАРІ 2323. НОВІ ПРОСТІ ЧИСЛА

ВИСНОВКИ

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

ДОДАТКИ

ВСТУП

Уперше запитуючи малюка: «Скільки тобі рочків?», він показує один пальчик. Найперше знайомство з числом виглядає кумедно й природньо для кожної людини. Виводячи цифри, ми й гадки не маємо, що то за скарби й скільки часу людство шліфувало їх, щоб ми могли ними скористатися.

Числа супроводжують нас усе життя, всі галузі, від побуту до космоса пронизані невидимою канвою зв’язків, які описуються числами. І якщо ми їх не бачимо, це означає лише те, що наших знань недостатньо.

Числа як колись, так і сьогодні мають багато таємниць, пояснити їх можна тільки строгими логічними міркуваннями. Особливо цікавим є те, що абстрактні числові викладки знаходять своє застосування в прикладних задачах, в описі природніх процесів, дозволяють робити прогнози, які справджуються. Але є задачі, які не зважаючи на елементарність їх постановки, ще й досі залишаються нерозв’язаними. Однією з таких задач є пошук простих чисел. Можливо, знайдена закономірність їх утворення відкриє людству нові можливості. Наша робота спирається на аналіз доступних джерел: ресурси Internet та науково-популярну літературу з математики. Так, ми розглянули праці Г. Бермана, М. Гарднера, А. Конфоровича дізналися про методи знаходження простих чисел, про результати досліджень простих чисел, які склалися в математиці. За основу взято спосіб відшукання простих чисел — «решето Ератосфена», що описаний І. Перельманом та Н. Віленкіним. Ми застосували його для проміжку натуральних чисел від 1 до 1000. Розглянули розподіл простих чисел на цьому проміжку — «скатертина Улама». У роботі прості числа погруповано за встановленими ознаками, як от: «близнюки», «дзеркальні числа», реп’юніти… Розглянуто галузі практичного використання простих чисел та проблеми в їх дослідженні.

Методом анкетування досліджено рівень обізнаності про прості числа серед різних вікових категорій. Популяризовано проект відшукання простих чисел.

Отож глибше ознайомлення з проблемами вивчення простих чисел, знайомство з теорією чисел - прекрасна школа для тих, хто живе в «цифровому світі» та мріє створювати штучний інтелект.

Об’єктом дослідження в роботі є прості числа.

Предметом дослідження є властивості простих чисел та їх розподіл.

Мета роботи полягає у вивченні властивостей простих чисел на основі реалізації алгоритмів виділення простих чисел; опрацюванні способів знаходження нових простих чисел; популяризація проблеми знаходження великих простих чисел.

Для досягнення мети необхідно розв’язати такі завдання:

розглянути натуральні числа й означити серед них прості;
навчитися знаходити прості числа, реалізувати «решето Ератосфена» та «скатертину Улама»;
зафіксувати цікаві властивості простих чисел;
знайти галузі використання простих чисел;
ознайомитися з проблемами вивчення простих чисел;
охарактеризувати актуальний на сьогодніпошук великих простих чисел;
популяризувати цю проблему шляхом опитування і пояснення серед однолітків.

РОЗДІЛ І. НАТУРАЛЬНИЙ РЯД ЧИСЕЛ. ДЕ ЖИВУТЬ ПРОСТІ ЧИСЛА.

Про те, як люди навчилися рахувати й вимірювати можна дізнатися з історії. Для того, щоб зафіксувати певну кількість потрібно було встановити відповідність між множиною предметів і множиною незмінних, постійних загальнодоступних елементів таких як: Сонце для позначення «одиниці»; парних предметів, таких як крила, вуха тощо для позначення «двійки». Іноді «три» означало весь навколишній світ людини – земне, небесне й підземне царства. Пальці виявилися прекрасним засобом для обчислень. Довгий час межею пізнання було число «сім» як зв’язок між зміною форми місячного диску або ж як сім напрямків руху із заданої точки. Зі зростанням виробництва додавалися об'єкти, які потрібно було рахувати в повсякденному житті, в зв'язку з чим змінювалися методи підрахунку. Людина навчилася рахувати двійками, трійками, п’ятірками і т. д. [7].

Зрозуміло, що для запису результатів вимірювань і підрахунку потрібно було мати визначені символи — перші числа. Особливістю чисел було те, що зі збільшенням їх кількості стало необхідним вводити щоразу нові знаки. Наприклад, греки могли записувати числа аж до 100 000 000 — міріади міріад, щоправда для цього їм необхідно було 29 знаків, а це весь алфавіт, кома і писана буква М. Попри незручності великий Архімед навчився називати велетенські числа, означивши 1 — одиницею першого періоду, міріаду міріад 100 000 000 — одиницею другого , міріаду міріад чисел другого періоду (100 000 000 000 000 000 ) він назвав одиницею третього періоду і так далі до міріадно міріадного періоду. Щоб уявити, яким великим є це число, достатньо сказати, що в нашому записі воно виглядало б як 1 з 800 000 000 нулів. Свої міркування вчений виклав у творі «Псамміт» або обчислення піску в просторі кулі, обмеженої нерухомими зірками[7].

Архімед уперше показав, що для будь‑якої кількості предметів, якою великою вона не була, можна знайти відповідне число; для будь‑якого числа можна вказати місце в ряду вже відомих чисел, побудувати ще більші числа й назвати їх. Це і є наукова система числення.

Наукове визначення числа дав Евклід в своїх «Початках»: «Одиниця є те, у відповідності, з чим кожна з існуючих речей називається однією. Число є безліч, складена з одиниць» [1]. Нуль з’явився пізніше, перший точно датований запис, в якому зустрічається знак нуля, відноситься до 876 року.

Довго людство добиралося до узагальнення чисел. Числа були записані по різному, але в будь‑якому вигляді вони були знаряддям для нумерації та підрахунку.

Вважається, що термін «натуральне число» вперше застосував римський державний діяч, філософ, автор робіт з математики й теорії музики Боецій (840 – 524 рр. до н.р.)

Сто віків знадобилося щоб вибудувати ряд натуральних чисел від 1 до нескінченності: 1, 2, 3, … Ідея про нескінченність простору й часу виникла дуже давно. Деякі давньогрецькі філософи говорили: «де б не став воїн, він може поставити свій спис ще далі» [7]. Спостереження показували, що за кожним натуральним числом іде наступне, більше на одиницю, й тільки тоді, коли люди навчилися записувати будь‑яке найбільше число, стало легше зрозуміти нескінченність.

Отже, очевидно, що назвати найбільше натуральне число неможливо. А от найменшим є одиниця, хоча в деяких країнах, наприклад, у Франції, найменшим натуральним числом вважають нуль. Нульовий індекс при підрахунку. В подальшому наявність нуля полегшує доведення деяких теорем.

Натуральні числа 1, 2, 3 … це упорядкована множина зі строго визначеною послідовністю. Це дозволяє порівнювати числа. Якщо число a зустрічається раніше, ніж b, то визначається відношення a < b.

У кінці XIX століття італійським математиком Д. Пеано були сформульовані й узагальнені властивості натуральних чисел.

Відомі арифметичні дії додавання і множення виконуються для всіх натуральних чисел і в результаті отримуємо завжди натуральне число. А от результат віднімання й ділення не завжди натуральне число. Якщо з відніманням проблема вирішується досить легко — від будь‑якого натурального числа, крім 1, можна відняти всі числа, які менші за нього й у результаті отримати натуральне число, при цьому кількість від’ємників буде завжди меншою ніж задане число, на 1. У випадку ділення з’являються результати, що характеризують кожне число окремо. Наприклад, одиниця має тільки один дільник, є числа, що мають два дільники: 1 і самого себе, і є числа, що мають три і більше дільники.

Простим є натуральне число, що має тільки два дільники — 1 і самого себе. Одиницю домовилися не відносити, ні до простих ні до складених чисел, решта – числа складені. Цікаво, що 2 є єдиним парним простим числом.

Найважливішим досягненням грецької античної математики є доказ двох основних тверджень, які приписують Евкліду: «Будь-яке натуральне число можна розкласти на прості множники» і «Ряд простих чисел нескінченний» [1].

Таким чином прості числа – це «цеглинки», з яких будуються всі інші натуральні числа». Отже виконання дії ділення над натуральними числами окреслює два завдання: визначити ознаки подільності, які дозволять дізнатися дільники числа, й визначити властивості простих чисел з метою їх знаходження.

Із часів стародавніх греків прості числа є настільки привабливими, як і невловимими. Простих чисел нескінченно багато. Найдавніше відоме доведення цього факту дав Евклід у «Началах». Його доведення може бути коротко відтворено так: уявімо, що кількість простих чисел скінченна. Перемножимо їх і додамо одиницю. Отримане число не ділиться на жодне зі скінченного набору простих чисел, тому що залишок від ділення на будь-яке з них дає одиницю. Значить, добуток має ділитися на деяке просте число, не включене до цього набору [1].

Можливо, Евклід був першим, хто визначив фундаментальність простих чисел. Приблизно за 300 років до нашої ери він розглядав парні досконалі числа (такі числа, як 6 і 28, які дорівнюють сумі своїх дільників: 6=1+2+3, 28=1+2+4+7+14). Він зрозумів, що всі парні досконалі числа 2^р-1(2ᴾ-1), тісно пов’язані з простими числами виду (2ᴾ-1) для деякого простого числа p (тепер числа (2ᴾ-1) називають числами Мерсенна). Отже, пошуки цих коштовностей розпочалися близько 300 року до нашої ери 7[].

РОЗДІЛ ІІ. «РЕШЕТО ЕРАТОСФЕНА», «СКАТЕРТИНА УЛАМА»

Спосіб який запропонував Ератосфен – «решето Ератосфена» ми вивчали на уроках математики. Він базується на викреслюванні чисел, кратних до заданого. Так ми можемо отримати початковий список простих чисел до певного значення.

Цей спосіб був удосконалений: решето Сундарама (1934 р.) – викреслювання чисел отриманих за пропонованою формулою, решето Аткіна – знаходження всіх простих чисел, менших за деяке задане число .

2.1 Пактична частина. Завдання 1

Спробувати відтворити способи знаходження простих чисел від 1 до 1000 за допомогою «решета Ератосфена» та візуалізувати розподіл знайдених простих чисел серед натуральних за допомогою «скатертини Улама»

«Решето Ератосфена»

Додаток 1

Результати:

Проміжок натурального ряду	Прості числа	Кількість простих чисел
Від 1 до 100	2; 3; 5; 7; 11; 13; 17; 19; 23; 29; 31; 37; 41; 43; 47; 53; 57; 61; 67; 71, 73;.79; 83; 89; 97;	25
Від 100 до 200	101; 103; 107; 109; 113; 127; 131; 137;139; 149; 151; 157; 163; 167; 173; 179; 181; 191; 193; 197; 199;	21
Від 200 до 300	211; 223; 227; 229; 233; 239; 241; 251; 257; 263; 269; 271; 277; 283; 293;	16
Від 300 до 400	307; 311; 313; 317; 331; 337; 347; 349; 353; 359; 367; 373; 379; 383; 389; 397;	16
Від 400 до 500	401; 409; 419; 421; 431; 433; 439; 443; 449; 457; 461; 463; 467; 479; 487; 491; 499;	17
Від 500 до 600	503; 509; 521; 523; 541; 547; 557; 563; 569; 571; 577; 587; 593; 599;	14
Від 600 до 700	601; 607; 613; 617; 619; 631; 641; 643; 647; 653; 659; 661;673; 677; 683; 691;	16
Від 700 до 800	701; 709; 719; 727; 733; 739; 743; 751; 757; 761; 769; 773; 787; 797;	14
Від 800 до 900	809; 811; 821; 829; 839; 853; 863; 877; 881; 883; 887;	15
Від 900 до 1000	907; 911; 919; 929; 937; 941; 947; 953; 967; 971; 977; 983; 991; 997.	14
Всього	простих чисел	168

«Скатертина Улама»

Додаток 2

Як бачимо, кількість знайдених чисел в кожній сотні змінюється за мірою їх наближення до 1000 і не виявляє ніякої закономірності. Зафіксувати, що прості числа розташовуються не хаотично, а утворюють орнаменти з діагональних ліній частково вдалося, але обраний нами проміжок замалий для візуалізації, оскільки кількість простих чисел на проміжках в кожній сотні зменшується.

Сучасні комп’ютери будують такі «вишиванки» для десятків мільйонів чисел, тому знайдена закономірність підтверджується. Однак міцний теоретичний фундамент підвести під цю «красу» поки не вдалося.

2.2. Пактична частина. Завдання 2

Проаналізувати виявлені прості числа.

Остання цифра простого числа, що має більше, ніж одну цифру, не може бути парною або 0, оскільки тоді й число було б і парним, а, отже, складеним; остання цифра не може бути і 5, поза як у цьому випадку можливе ділення на 5, а, отже, число — складене. Таким чином, останньою цифрою простого числа може бути тільки 1, 3, 7 або 9.
Найбільшим числом на обраному проміжку є 997.
Два найменших простих числа 2 і 3 є послідовними натуральними числами, інших послідовних натуральних простих чисел немає. Легко довести, що з кожних двох послідовних натуральних чисел одне є парним, що означає —воно складене.
Пари простих чисел, що відрізняються на 2 називаються близнюками. Таких ми виявили 35 пар: (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71,73), (101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193), (197, 199), (227, 229), (239, 241), (269, 271), (281, 283), (311, 313), (347, 349), (419, 421), (431, 433), (461, 463), (521, 523), (569, 571), (599, 601), (617, 619), (641, 643), (659, 661), (809, 811), (821, 823), (827, 829), (857, 859), (881, 883).
Прості трійні, що попарно різняться на 2, знайдено 2: (2, 3, 5), (3, 5, 7).
Прості триплети виду (р, р+2, р+6) або (р, р+4, р+6) знайдено 30: (5, 7, 11), (7, 11, 13), (11, 13, 17), (13, 17, 19), (17,19, 23), (37, 41, 43), (41, 43, 47), (67, 71, 73), (97, 101,103), (101, 103, 107), (103, 107, 109), (107, 109, 113), (191, 193, 197), (193, 197, 199), (223, 227, 229), (227, 229, 233), (277, 281, 283), (307, 311, 313), (311, 313, 317), (347, 349, 353), (457, 461, 463), (461, 463, 467), (613, 617,619), (641, 643, 647), (821, 823, 827), (823, 827, 829), (853, 857, 859), (857, 859, 863), (877, 881, 883), (881, 883, 887)
Одне просте число, всі цифри якого одиниці — 11. Наступне таке число записується 19‑тьма одиницями. Є ще більші. Такі числа називають реп’юніти.
Знайдені прості числа, які лишаються простими при кожній перестановці їх цифр. Серед трьох значних такими є числа: 113, 131, 311; 199, 919, 991; 337, 373, 733, серед двозначних такими є дзеркальні числа: 11, 13 і 31, 17 і 71, 37 і 73, 79 і 97. До речі, 73 – 21‑е просте число, його дзеркальне число 37 є 12‑м, а дзеркальне 21 є добутком 7 і 3
Виявили числа паліндроми: 101, 131, 151, 181, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929.
Також ми виявили прості сильні числа. Число є сильним, якщо воно більше, ніж середнє арифметичне найближчих простих згори і знизу (інакше кажучи, воно ближче до наступного ніж, до попереднього). Наприклад, 17 ‒ це сьоме просте число. Шосте і восьме, 13 і 19, їхня сума становить 32, половина 16. Тобто 17 ‒ сильне просте. Отримали прості сильні числа: 11, 17, 29, 37, 41, 59, 67, 71, 79, 97, 101, 107, 127, 137, 149, 163, 179, 191, 197, 223, 227, 239, 251, 269, 277, 281, 307, 311, 331, 347, 367, 379, 397, 419, 431, 439, 457, 461, 479, 487, 499, 521, 541, 557, 569, 587, 599, 613, 617, 631, 641, 659, 673, 701.
Прагнучи до узагальнення математики, записували формули, за якими можна отримати прості числа. Але отримані результати не завжди однозначні, тому необхідна додаткова перевірка . Числа називали іменами винахідників.
Серед наших є прості числа Мерсена ‒ 3, 7, 31, 127, прості числа Ферма ‒ 3, 5, 17, 257, прості числа Жермен ‒ 2, 3, 5, 11, 23, 29, 41, 53, 83, 89, 113, 131, 173, 179, 191, 233, 239, 251, 281, 293, 359, 419, 431, 443, 491, 509, 593, 641, 653, 659, 683, 719, 743, 761, 809, 911, 953, прості Вільсона ‒ 5, 13, 563, факторіальні прості ‒ 2, 3, 5, 7, 23, 719.

Цікаво: знайдено число 379009 є простим числом. Це також схоже на слово Google, якщо ви введете його в калькулятор і подивитесь на нього догори ногами!

РОЗДІЛ ІІІ. ВИКОРИСТАННЯ ПРОСТИХ ЧИСЕЛ. ВІДКРИТІ ПИТАННЯ У ВИВЧЕННІ ПРОСТИХ ЧИСЕЛ

Давно минули часи коли вчення про числа було надбанням обраних. Вони можуть гіпнотизувати людей, що вірять в нумерологію, і практично допоиагати тим, хто вирішує реальні питання. Числа керують світом, бо саме їх властивості покладені в основу законів, що описують всі процеси.

В математиці, запис натурального числа у вигляді добутку простих множників називається розкладом числа на прості множники. Канонічним розкладанням натурального числа на прості множники називають такий запис розкладу, коли основи степенів простих множників записуються в порядку зростання. Такий розклад дозволяє швидко знаходити всі дільники для даного числа, визначати найменше спільне кратне (НСК), та найбільший спільний дільник (НСД).

Знаходити прості дільники даного натурального числа досить громіздка операція.

1800

900

450

225

176

Маємо: 1800= 2³* 3²*5³та 176 = 2³• 11

За розкладом легко визначити всі дільники чисел. Для числа 1800 ̶ 1800, 900, 450, 225, 200, 120, 75, 25, 45, 40, 15, 9, 8, 5, 4, 3. Для числа 176 ̶ 176, 88, 44, 11, 22, 8, 4

Для обчислення НСД обираємо спільне в канонічному записі чисел. НСД (1800, 176) =2³=8

Два числа, що мають найбільший спільний дільник рівний одиниці називаються взаємно простими числами. Для взаємно простих чисел найменше спільне кратне дорівнює їх добутку.

Для обчислення НСК обираємо всі різні елементи з двох канонічних розкладів чисел. НСК (1800, 176) =2³• 11•3²•5²=19800

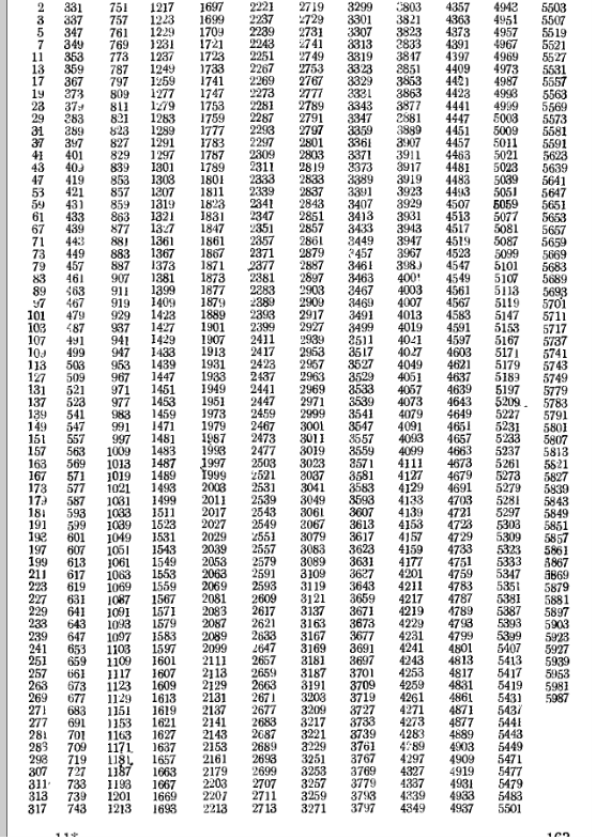
Для розкладання на множники великих чисел, наприклад 27217 = 17•1601 або 75815 = 101•751 використовують таблиці простих чисел. Додаток 4. Та таблиці розкладів на множники для складених чисел. У 1909 році з’явилася таблиця Лемера, що доходила до 10 000 000. Пізніше їх було ще більш розширено. Для великих складених чисел у таблиці задається лише один простий дільник. В отриманому добутку наступне складене число знайде свій простий дільник знову в таблиці. Значно полегшує процес розкладу онлайн калькулятор для розкладу чисел на прості множники [8].

Закономірності, що пов’язують прості числа нерідко стають основою фокусів і вражають пересічного глядача.

Наприклад:

Задумайте якесь трицифрове число. Допишіть до нього справа таке саме число. Знайдене шестицифрове число поділіть на 7. Поділіть знайдену частку на 11. Нову частку розділіть на 13. Виконавши ці операції ви отримаєте задумане число.

Ідея цього фокуса дуже проста: приписуючи справа до деякого трицифрового числа таке саме число, ми неначе множимо це число на 1001, наприклад:

537537=537000+537=537*(1000+1) =537*1001. Але 1001=7*11*13

Отже, цей математичний фокус ґрунтується на знаходженні розкладу цілого числа на прості множники [5].

Прості числа і взаємно прості числа широко застосовуються в техніці й механіці. Наприклад у ланцюговій передачі, як правило, кількість ланок ланцюга й зубів зірочки виражаються взаємно простими числами. Завдяки цьому кожен з зубів стикається з кожною ланкою ланцюга по черзі, механізм менше зношується.

У музиці прості числа пояснюють ефекти, що викликані повторенням складних ритмічних композицій.

У біології існує гіпотеза, що цикади еволюціонували таким чином, щоб знаходитися в сплячці протягом періоду, що охоплює 7, 13, 17 років ̶ прості числа. Завдяки чому вони рідше зустрічаються з хижаками і паразитами, що мають дво-, три-, чотири-, шестирічними циклами. Це пояснює найменше спільне кратне, що є добутком числових значень циклів їх розвитку.

В астрономії прості числа підказали орбіти руху планет. Дозволили прорахувати наявність планети Нептун, існування якої і підтвердили в зазначеному місці.

Астероїд, назва якого Прайм, означає просте число (англ. prime number ̶ просте число), названий на честь числа 7919, яке є тисячним простим числом.

В криптографічних системах властивості простих чисел є основою безпеки електронних комунікацій. Використовуються прості числа для створення ключів для кодування інформації. Завдяки простим числам ми вільно користуємося послугами інтернет‑магазинів, маємо цифровий підпис, тримаємо в безпеці наші смартфони.

Досі існує багато відкритих запитань щодо простих чисел, найвідоміші з яких:

Проблема Гольдбаха ‒ довести або спростувати, що кожне парне число більше двох може бути представлене у вигляді суми двох простих чисел, а кожне непарне число більше 5 може бути представлене у вигляді суми трьох простих чисел.
Чи нескінченна множина «простих близнюків» ‒ простих чисел, різниця між якими дорівнює 2?
Чи вірно, що між числами n² і (n + 1)² завжди знайдеться просте число?
Чи нескінченна множина простих чисел Жермена?
Чи нескінченна кількості простих чисел у багатьох цілочисельних послідовностях, включаючи числа Фібоначчі, числа Ферма і т. д.
Скільки існує простих чисел, усі цифри яких одиниці?
Скінченна чи нескінченна множина простих чисел, перша і остання цифра яких дорівнює одиниці, а всі інші цифри – нулі?
Скільки існує простих чисел, серед цифр яких немає жодного нуля?

Однією з найвідоміших проблем теорії чисел є проблема Гольдбаха. Історія виникнення її така.

Христіан Гольдбах (1690 – 1764 рр.) – математик, член Петербурзької Академії наук, тривалий час листувався з Леонардом Ейлером. У своєму листі від 7 червня 1742 року він зауважив: «Мабуть, кожне число, більше за одиницю, є сумою трьох простих чисел». 30 червня 1742 року Ейлер відповів йому: «Те, що кожне парне число є сумою двох простих чисел, я вважаю цілком правильною теоремою, хоча й не можу довести її». Це твердження і ввійшло в історію під назвою «проблема Гольдбаха».

Перевіривши цю гіпотезу на прикладах, переконався в емпіричній очевидності її. Насправді, 4=2+2, 6=3+3, 8=5+3, 10=7+3, 12=7+5, ..., 100=97+3. ..., 1000=809+191 тощо [].

Труднощі пояснюються тим, що поняття простого й парного чисел визначаються в термінах множення. А в умові йдеться про операцію додавання.

Довгий час «проблема Гольдбаха» була зовсім недоступною. Було доведено, що кожне натуральне число можна подати у вигляді суми не більш як 800000 простих чисел. Трохи пізніше кількість доданків було зменшено до 67.

У 1937 році видатний математик І. М. Виноградов, користуючись складними аналітичними методами довів, що кожне досить велике непарне число є сумою трьох простих чисел [2].

Отже прості числа знаходяться під пильним контролем математиків, визначено безліч властивостей простих чисел. Досліджено зв’язки з іншими числами і вони мають безліч таємниць.

РОЗДІЛ ІV. САФАРІ 2323. НОВІ ПРОСТІ ЧИСЛА

На практиці замість отримання списку простих чисел найчастіше потрібно перевірити, чи є дане число простим. Алгоритми, які вирішують це завдання, називають тестами простоти. Існує безліч конкретних та ефективних тестів для деяких класів чисел. Наприклад, для перевірки на простоту чисел Мерсенна використовують тест Люка ‒ Лемера, а для перевірки на простоту чисел Ферма ‒ тест Пепіно.

Прості числа Мерсенна названо на ім'я французького ченця Марина Мерсена, який вивчав ці числа більше 350 років тому. Відшукання нових простих чисел справа почесна і серйозна, адже завдяки їм Ви можете опинитися в списках першовідкривачів.

Great Internet Mersenne Prime Search (GIMPS) великий проєкт пошуку простих чисел Мерсенна в Інтернеті, його було створено в січні 1996 року для виявлення нових світових рекордів простих чисел Мерсенна. GIMPS використовує потужність тисяч персональних комп’ютерів для пошуку «голки в копиці сіна».

21 грудня 2018 року організація Great Internet Mersenne Prime Search (GIMPS) зафіксувала виявлення найбільшого з відомих простого числа (2 ^{825 899 33} – 1), що складається з 24 863 048 знаків. Комп'ютер добровольця Патріка Ляроша вирахував його 7 грудня 2018 року. За своє відкриття він отримав від GIMPS дослідницьку нагороду 3000 доларів.

Нове просте число, також відоме як M82589933, обчислено перемноженням 82 589 933 двійок і відніманням одиниці. Воно перевершує попереднє рекордне просте число більше ніж на півтора мільйони розрядів. Це всього п'ятдесят перше відкрите просте число Мерсенна; обчислення кожного наступного стає складнішим. Для пошуку цих простих чисел завантажують безкоштовну програму, яка дає можливість виграти грошовий приз, за умови відшукання нового простого числа. Створено веб-сайт, присвячений найбільш відомим простим числам, що знайомить з історією простих чисел Мерсена. Наступною великою метою GIMPS є розіграш нагороди в розмірі 150 000 доларів, яка буде вручена за знаходження простого числа зі 100 000 000 десяткових розрядів [4].

Для визначення рівня популярності простих чисел ми створили анонімний опитувальник.

Додаток 3

РЕЗУЛЬТАТИ ОПИТУВАННЯ

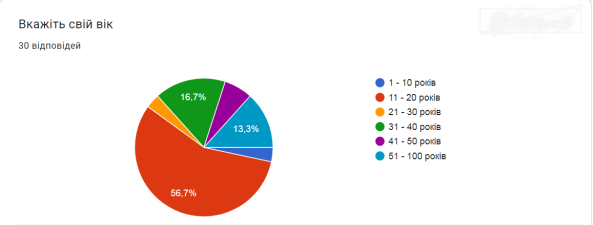
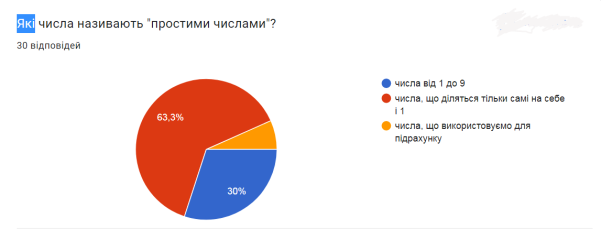
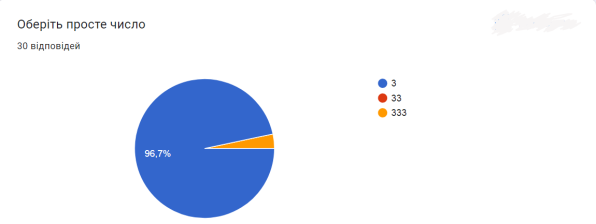
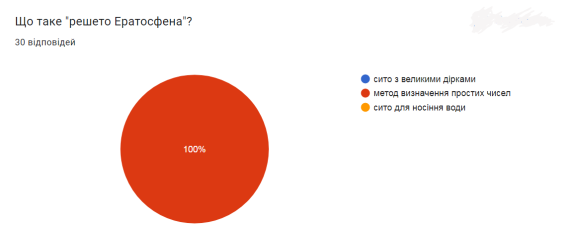
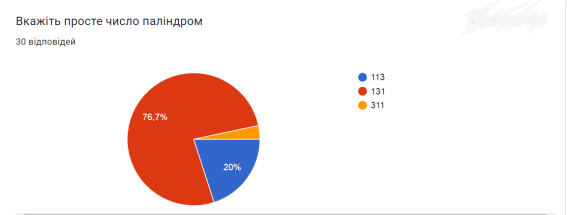
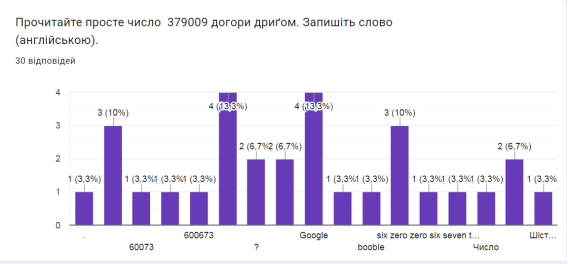
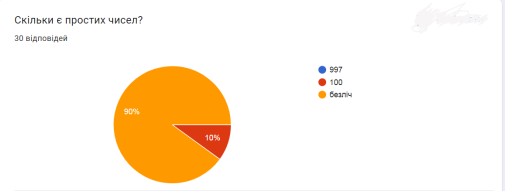
В опитуванні брали участь 30 респондентів. Отримані результати вказують, що найбільш активними учасниками були респонденти віком від 10 до 29 років та від 40 до 50 років. 60% відповідей щодо визначення простих чисел ‒ вірні. На 96,7% правильно відповіли всі в завдані на визначення простих чисел. «Решето Ератосфена» ‒ 100%‑во визначено, як метод знаходження простих чисел. До розв’язку креативних завдань респонденти готові на 13%. Як бачимо серед користувачів цифрових технологій прості числа не викликають широкого інтересу, але вони є основою безпеки для кожного володаря смартфона.

ВИСНОВКИ

У результаті дослідження було з’ясовано, що простих чисел є нескіннченна кількість. Проміжки, що мість прості числа нескінченно зростають і не підпорядковані законам строгого розподілу. На сьогодні, обчислювальна техніка значно розширила можливості дослідження і знаходження простих чисел. Складено таблиці розкладу чисел на прості множники. Створено онлайн калькулятори для розкладу великих складених чисел на прості множникина.

Вони широко використовуються для розв’язуваня задач, що є математичними моделями життєвих ситуацій. Встановлено, що на сьогодні інтерес до простих чисел підвищився. Вони стали основою сучасних теорій, наприклад в астрономії, криптографії чи біології.

Перед математиками стоїть дуже багато цікавих задач пов’язаних з простими числами. Їх вивчають по одному і цілими послідовностями, але вони так і не відкрили таїни свого походження.

Пошук простих чисел Мерсена продовжується. Вони довгий час були абсолютно безкорисними, але потреби «цифрової доби» вже почали відкривати браму до великої скарбниці простих чисел.

Можливо в майбутньому саме прості числа будуть візитною карткою людства і використовуватимуться для комунікації з позаземними формами життя.