Творческая работа

по теме:

 

для факультативного курса

учащихся 9-го класса

 

 

 

                                                                      Выполнила

Учитель математики

Петропавловского лицея №1

Полозенко Е.С.

                                       

 

 

 

 

                        

Содержание

1.Индукция – метод познания истины

1.1.Индуктивные умозаключения………………………………..1

• Виды индукции…………………………....................................5
• Упражнения………… ……………………....................................8

1.2. Связь прошлого с настоящим ……………………...............10

1.3.Индукция – как эвристический прием……………...............13

• Индукция в математике…………………………………………13
• Индукция при поиске математических закономерностей…………………………………………………15

2.Метод математической индукции

2.1.Принцип математической индукции…………......................17

2.2. Применение метода математической индукции для доказательства справедливости тождеств………………………21

2.3.Применение метода математической индукции для вывода некоторых математических закономерностей и доказательства их справедливости…………………………………………….....23

2.4.Решение неравенств с помощью метода

математической индукции……………………………................25

2.5.Делимость чисел и метод математической индукции…………………………………………………………27

2.6.Применение метода математической индукции

      для решения геометрических задач………………...............29

2.7.Занимательные задачи на индукцию……………………….30

2.8.Парадокс изобретателя………………………………………38

2.9.Контрольная работа по теме “математическая индукция”………………………………………………………...39

Заключение……………………………………………………….41

Приложение…………………………………………………........42

Использованная литература…………………………………………..48

 

1.Индукция – метод познания истины

1.1.Индуктивные умозаключения

Математика, как известно, наука доказательная, или дедуктивная (от лат. Deductio – выведение). Однако это только одна из ее сторон. Изложенная в законченной форме, математика выглядит как чисто дедуктивная, состоящая только из доказательств. Но прежде чем провести доказательство во всех деталях, нужно догадаться об идее, лежащей в его основе, нужно сопоставлять наблюдения и следовать аналогиям. Результат творческой работы математика – доказательное и правдоподобное –  дополняют друг друга. И так как в решении любой задачи присутствует крупица открытия, то в нем должно найтись место для догадки, для правдоподобного умозаключения.

Как сказал выдающийся советский математик А.Н.Колмогоров: «Некоторым математика представляется нагромождением искусственных рецептов, правил, по которым неведомо почему можно получать нужные результаты. На самом деле математика проще, чем иногда думают… Попытайтесь заменить запоминание пониманием! Тогда и запомнить правила будет не так трудно».

Умозаключение – это процесс рассуждения, посредством которого из одного или нескольких суждений выводится новое суждение. Исходные суждения называются посылками умозаключения, а новое суждение, полученное из посылок, называется заключением. При этом если из условия вытекает следствие, условие является достаточным, если условие само вытекает из следствия – условие является необходимым. Умозаключения делятся на дедуктивные, индуктивные и умозаключения по аналогии. Рассмотрим индуктивные умозаключения.

Метод, посредством которого на основе повторяющегося признака отдельных явлений делается обобщенное заключение, называется индуктивным умозаключением или индукцией.

Если вы хотите наблюдать жизнь птиц так, чтобы была некоторая возможность получить интересные результаты, то вы должны быть в какой-то степени знакомы с птицами, интересоваться ими. Точно так же, если вы хотите наблюдать числа, вы должны интересоваться ими и в какой-то степени быть знакомы с ними.

 Вы должны различать четные и нечетные числа, должны знать квадраты 1, 4, 9, 16, 25, … и простые числа 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, … Даже со столь скромными знаниями вы смогли бы подметить кое-что интересное.

Случайно вы наталкиваетесь на соотношения

3+7=10, 3+17= 20, 13+17=30

и замечаете между ними некоторое сходство. Вам приходит в голову, что числа 3, 7, 13 и 17 являются нечетными простыми числами. Сумма двух нечетных простых чисел есть обязательно четное число; действительно числа 10, 20 и 30 – четные. А что можно сказать о других четных числах? Ведут ли они  себя подобным образом? Первое четное число, являющееся суммой двух нечетных простых чисел, есть,  конечно, 6=3+3.

Двигаясь дальше, находим, что

8=3+5,

10=3+7=5+5,

12=5+7,

14=3+11=7+7,

16=3+13=5+11.

Всегда ли так будет продолжаться? Как бы то ни было, частные случаи, которые мы наблюдали, наводят на мысль об общем утверждении: любое четное число, больше чем 4, представимо в виде суммы двух нечетных простых чисел. Поразмыслив об исключительных случаях – числах 2 и 4, которые не могут быть расщеплены  в сумму двух нечетных простых  чисел, мы можем предпочесть следующее менее непосредственное утверждение: любое четное число, не являющееся ни простым числом, ни квадратом простого числа, представимо в виде суммы двух нечетных простых чисел.

Итак, нам удалось сформулировать предположение. Мы нашли это предположение с помощью индукции. Иными словами, оно возникло у нас в результате наблюдения, было указано отдельными частными примерами.

Эти указания являются довольно легковесными; у нас есть лишь очень слабые основания верить в свое предположение. Мы можем, однако, найти некоторое утешение в том факте, что Гольдбах, математик, впервые высказавший это предположение более двухсот лет тому назад, не обладал для этого сколько-нибудь более серьезными основаниями.

Возвратимся на минуту к числу 60. После того как были испытаны простые числа 3, 5 и 7, мы можем испытать остающиеся простые числа до 30. Мы получим, таким образом, все разложения 60 в сумму двух простых чисел:

60=7+53=13+47=17+43=19+41=23+37=29+31.

Посмотрим теперь снова на предыдущее рассуждение и попытаемся заметить в нем черты, типичные для процесса индукции.

Высказав предположение, мы пытались выяснить, является ли оно верным или ошибочным. Наше предположение было утверждением общего характера, возникшим из некоторых частных примеров, в которых оно оказалось верным.

Этот ли принцип лежит в основе индукции?

Взглянем снова на пример индуктивного рассуждения, который мы разобрали довольно подробно. Мы начали с того, что подметили аналогию трех соотношений:

3+7=10, 3+17=20, 13+17=30,

мы обобщили, поднявшись  от 3, 7, 13 и 17 ко всем простым, а от 10, 20 и 30 ко всем числам, затем мы снова специализировали, спустившись к испытанию отдельных четных чисел, как например 6, или  8, или 60.

Этот первый пример крайне прост. Он совершенно правильно иллюстрирует роль обобщения, специализации и аналогии в индуктивном рассуждении. Однако мы должны исследовать более яркие иллюстрации, и до этого мы должны рассмотреть обобщение, специализацию и аналогию, эти великие источники открытия.

Обобщение есть переход от рассмотрения данного множества предметов к

рассмотрению большего множества, содержащего данное. Например, мы обобщаем, когда переходим от рассмотрения треугольников к рассмотрению многоугольников с произвольным числом сторон. Мы обобщаем также, когда переходим от изучения тригонометрических функций острого угла к изучению тригонометрических функций произвольного угла.

Можно заметить, что в этих двух примерах обобщение осуществлялось в двух характерно различных направлениях. В первом примере, в переходе от треугольников к многоугольникам с n сторонами, мы заменяем постоянную переменной, фиксированное число 3 произвольным числом n (ограниченным только неравенством n3). Во втором примере, в переходе от острых углов к произвольным углам , мы отбрасываем ограничение, именно  ограничение .

Мы часто обобщаем, переходя от одного лишь предмета к целому классу, содержащему этот предмет.

Специализация есть переход от рассмотрения данного множества предметов к рассмотрению меньшего множества, содержащегося в данном. Например, мы специализируем, когда переходим от рассмотрения правильных многоугольников, когда переходим от правильных многоугольников с n сторонами к правильному (или равностороннему) треугольнику.

Эти два последовательных перехода осуществлялись в двух характерно различных направлениях. В первом переходе, от многоугольников к правильным многоугольникам, мы ввели ограничение, именно потребовали, чтобы все стороны и все углы многоугольника были равны. Во втором переходе мы заменили переменный предмет конкретным, поставили 3 вместо переменного целого числа n.

Очень часто мы производим специализацию, переходя от целого класса предметов к одному предмету, содержащемуся  в этом классе. Например, когда мы хотим проверить некоторое общее утверждение относительно простых чисел, мы выбираем какое-нибудь простое число, скажем 17, и исследуем, справедливо ли это общее утверждение именно для числа 17.

Аналогия есть некоторого рода сходство. Она, можно сказать, есть сходство, но на более определенном и выражаемом с помощью понятий уровне. Однако мы можем выразиться несколько более точно. Существенное различие между аналогией и другими видами сходства заключается в намерениях думающего. Сходные предметы согласуются между собой в каком-то отношении. Если вы намереваетесь свести это отношение, в котором они согласуются, к определенным понятиям, то вы рассматриваете эти сходные предметы как аналогичные.

Рассматривая в музее скелеты различных млекопитающих, вы можете обнаружить, что все они страшны. Если в этом все сходство, которое вы между ними обнаружили, то вы видите не такую уж сильную аналогию. Однако вы можете подметить удивительно много говорящую аналогию, если рассмотрите руку человека, лапу кошки, переднюю ногу как состоящие из сходных частей, имеющие сходное отношение друг к другу.

Последний пример иллюстрирует наиболее типичный случай выясненной аналогии; две системы аналогичны, если они согласуются в ясно определенных отношениях соответствующих частей.

Одно из значений слова «аналогия», есть «пропорция». Действительно система двух чисел 6 и 9 «аналогична» системе двух чисел 10 и 15, поскольку отношения соответствующих членов этих двух систем согласуются:

6 : 9=10 : 15

Пропорциональность, или согласованность отношений соответствующих частей, которую мы интуитивно видим в геометрически подобных фигурах, является наводящим на размышления случаи аналогии.

Всегда желательно предугадать результат или, по крайней мере, некоторые его черты с той или иной степенью правдоподобия. Такие правдоподобные догадки часто основываются на аналогии.

Заключения по аналогии есть самый обычный вид рассуждения. Оно при­водит нас к более или менее правдоподобным предположениям, которые могут подтвердиться опытом или более строгими рассуждениями. Химик, экспериментирующий на животных, чтобы пред­сказать действие своих препаратов на человеке, делает вы­воды по аналогии. Эти заключения, связывающие много параллельных фактов, обладают большей убедительно­стью, чем сделанное на основании меньшего числа фактов, однако их качество важнее их количества. Выясненная аналогия обладает большей ценностью, чем отдаленное сходство; факты, приведенные в систему, в состоянии натолкнуть нас на более глубокие идеи, чем факты, собранные случайным образом.

И сейчас, все предшествующее наводит на мысль, что рассмотренные факты допускают распространение на n-мерный случай. Кажется невероятным, что то, что оказалось верным для трех первых чисел (n=1, 2, 3) окажется неверным для больших значений n. Это предположение есть «заключение по индукции», оно иллюстрирует то, что индукция естественным образом основывается на аналогии.

Можно сделать вывод, что индуктивные умозаключения строятся из наблюдений, путем обобщения знаний меньшей общности, опираясь на некоторые их особенности, к знаниям большей общности. Они дают, как правило, лишь вероятностные заключения, поскольку, если заключение содержит новую информацию, превосходящую информацию посылок, оно не может непосредственно следовать из посылок и его истинность остается под вопросом, требуя дополнительных подтверждений.

Так же, как логика дедуктивных умозаключений основана на том что, ничто частное не существует вне общего, логика индуктивных умозаключений основана на том что, общее не существует самостоятельно, любые закономерности обнаруживаются, проявляясь в частностях.

Индукция упрощает мир, облегчая его понимание, не будь ее, человечество, в своих познаниях, не двинулось бы дальше бесчисленного набора, не имеющих значения фактов и, до сих пор бы лазило по деревьям (если бы не вымерло). Все крупные гипотезы и основные законы науки построены методом обобщения частных случаев. Только дополнительные (частные) законы, выводимые из основных, получают методом дедукции. Можно сказать что, индуктивные умозаключения несут в себе зерно гениальности и остаются для многих недоступными только из-за боязни взять ответственность на себя и быть осмеянными. А между тем, незначительное, на первый взгляд обобщение может привести к революционному прорыву в какой-либо сфере человеческой деятельности. Однако, поскольку индукция – это обобщение, никогда нельзя знать наверняка что, оно не поспешно, тем более что, к ней часто прибегают глупцы и наглецы, тем самым, компрометируя сам метод индукции.

Слово «индукция» означает «наведение» и если в электродинамике она наводит ток, то в логике, наводит мысль, в чем сходна с аналогией.

• Виды индукции

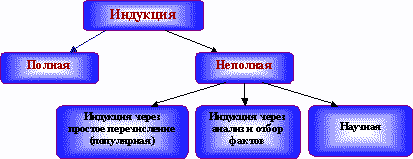
Полная индукция не имеет принципиального различия с дедукцией и дает достоверное знание, строя заключение о каком-либо понятии и всех его элементах на основе анализа каждого из них, рассматривая их все и используя посылками единичные суждения (в том числе общие). Ее построение такое:

A имеет признак θ B имеет признак θ C1 имеет признак θ C2 имеет признак θ И все D имеет признак θ … и последний Z, так же, имеет признак θ A, B, C и другие, вплоть до Z имеют признак θ Все они принадлежат к понятию λ Других λ не существует Все λ имеют признак θ

Для ее использования необходимо:

1.       Точно знать число рассматриваемых единиц.
2.       Убедится что, устанавливаемый признак (θ) действительно принадлежит каждому элементу этого класса (λ).

Например, раньше астрономы делали ошибочный вывод, что все планеты и спутники движутся в одном направлении потому, что учёным ещё не были известны спутники самых отдалённых от солнца планет, которые движутся в другом направлении.

Выведение истинных заключений полной индукцией часто требует огромного числа дополнительных фактов для подтверждения всех ее следствий, что сильно ограничивает область ее применения, но иногда интерес, вызываемый ею, больше лени, а ожидаемые последствия, ценнее текущих расходов. Главный ее минус – некоторая доля вероятности что, не все факторы учтены, а значит, что индукция может оказаться неполной.

Неполная индукция дает вероятностное заключение и применяется при невозможности рассмотрения всех без исключения случаев. К неполной индукции относится перечислительная, аналитическая, научная индукции.

Перечислительная (популярная) индукция осуществляется на основании повторяемости одного и того же признака у ряда факторов и отсутствия противоречивого случая, выводом что, все факторы этого рода имеют указанный признак. Так, обнаруживая массу у всех известных ему предметов, Ньютон обобщил: «Все тела имеют массу». Но подобные обобщения не всегда правомерны. Примером поспешного обобщения служат лебеди: европейцы считали что, все лебеди белые, пока не обнаружили в Австралии черных. Поскольку перечислительная индукция допускает исключения из правил, ее выводы лишь правдоподобны, а не достоверны. Уверенность в их истинности растет с появлением новых подтверждений, но утверждение ее возможно лишь через другие способы умозаключений.

На основе популярной индукции народ вывел немало примет:

•                     Ласточки низко летают – быть дождю;
•                     Если закат солнца красный, то завтра будет ветреный день и т.д.

Аналитическая индукция с целью исключить случаи поспешного обобщения предполагает выбор наиболее типичных факторов, разнородных по времени и другим возможным условиям. В индукции через анализ и отбор фактов стремятся исключить случайность обобщений, так как изучаются планомерно отобранные, наиболее типичные предметы - разнообразные по времени, способу получения и существования и другим условиям.
Так вычисляют среднюю урожайность поля, судят о всхожести семян, о качестве больших партий товаров и т. д.
Например, при изучении качества рыбных  консервов банки берутся 

•                     из разных холодильников,
•                     выпущенные в разные сроки,
•                     различными заводами,
•                     из различных сортов рыбы.

Изучая свойства серебра, люди обнаружили, что

•                     серебро активирует углерод,
•                     уничтожает бактерии.

С помощью серебра очищают воду. Хирурги применяют серебросодержащие кремы при лечении ожогов и скрепляют кости цементом, который содержит бактерицидные соли серебра. Многим тысячам людей, пострадавшим от тяжелых ожогов, жизнь спасли препараты, включающие серебро. Так на основе индукции через отбор, планомерно изучая свойства серебра, люди сделали правильные заключения о возможности и необходимости применения серебра при лечении различных заболеваний.

Научной индукцией называется такое умозаключение, в котором на основании познания необходимых признаков или необходимой связи части предметов класса делается общее заключение о всех предметах класса.  Научная индукция, так же как полная индукция,  даёт достоверное заключение. Достоверность заключений научной индукции, хотя она и не охватывает все предметы изучаемого класса, а лишь их часть (и притом небольшую), объясняется тем, что учитывается важнейшая из необходимых связей - причинная связь. Так с помощью научной индукции делается заключение: «Всем людям для жизнедеятельности необходима влага». В частности, Ю.С.Николаев и Е.И.Нилов в книге «Голодание ради здоровья» пишут, что человек без пищи (при полном голодании) может прожить 30-40 дней, а воду он должен пить ежедневно. Без воды человек не может жить, ибо процесс обезвоживания организма ведёт к нарушению внутриклеточного обмена веществ, что приводит к смерти. Голодание же, проводимое под наблюдением врачей, наоборот, способствует при многих заболеваниях (например: хроническом нефрите, гипертонической болезни, стенокардии, атеросклерозе, бронхиальной астме) выздоровлению.

Причиной излечения этих болезней при длительном голодании является изумительная саморегуляция организма во время полного лечебного голода, когда осуществляется общебиологическая перестройка организма больного человека.

Обычное переедание, которое ежедневно задает огромную, совершенно ненужную работу желудку и сердцу, - главная причина многих болезней, усталости, ранней дряхлости. Применение научной индукции позволило сформулировать общие суждения и научные законы (физические законы Архимеда, Кеплера, Ома и др.)

Методика научной индукции приближается к дедуктивной, замыкая круг возможного мышления (дедукция → аналогия → индукция → дедукция).

Дедуктивное умозаключение применяется нами всякий раз, когда требуется рассмотреть какое-либо  явление на основании уже известного нам общего положения и вывести в отношении этого явления необходимое заключение. Нам известен, например, следующий конкретный факт – «данная плоскость пресекает шар» и общее правило относительно всех плоскостей, пересекающих шар, – «всякое сечение шара плоскостью есть круг». Применяя это общее правило к конкретному факту, правильно мыслящий человек придет к одному и тому же выводу: «значит, каждая плоскость есть круг».

Ход рассуждения при этом будет таков: если данная плоскость пересекает шар, а всякое сечение шара плоскостью есть круг, то, следовательно, и данная плоскость есть круг. В итоге данного умозаключения получено новое знание о данной плоскости, которое не содержится непосредственно ни в первой мысли («данная  плоскость пересекает шар»), ни во второй мысли («всякое сечение плоскостью есть круг»), взятых отдельно друг от друга. Вывод о том, что «данная плоскость есть круг, получен в результате сочетания этих мыслей в дедуктивном умозаключении.

Дедукция играет большую роль в нашем мышлении. Во всех случаях, когда конкретный факт мы подводим под общее правило и затем из общего правила выводим какое-то заключение в отношении этого конкретного факта, мы заключаем в форме дедукции. И если посылки истинны, то правильность вывода будет зависеть от того, насколько строго мы придерживались правил дедукции.

Всякая дедукция является результатом предварительного индуктивного изучения материала.  В свою очередь индукция является подлинно научной только тогда, когда изучение отдельных частных явлений основано на знании уже известных каких-то общих законов развития этих явлений. При этом процесс познания  начинается и идет одновременно  дедуктивно и индуктивно. Этот правильный взгляд на соотношение индукции и дедукции был впервые доказан марксистской философией. «Индукция и дедукция,– писал Ф. Энгельс в «Диалектике природы»,– связаны между собой столь же необходимым образом, как синтез и анализ. Вместо того, чтобы односторонне превозносить одну из них до небес за счет другой, надо стараться применять каждую

 на своем месте, а этого можно добиться лишь в том случае, если не упускать из виду их связь между собою, их взаимное дополнение друг друга».

• Упражнения

1.Даны умозаключения:

А) Поскольку Чарли Чаплин и многие другие талантливые режиссеры не получали «Оскар», то получившие, заработали его не столько своим талантом, сколько вкусом организаторов фестиваля; вполне вероятно что, многие из них были и вовсе бездарны.

Б) Все металлы пластичны.

Висмут – металл.

Следовательно, висмут пластичен.

В) Все сочинения Пушкина нельзя прочитать за одну ночь. “Медный всадник”– сочинение Пушкина.

Следовательно, “Медный всадник” нельзя прочитать за одну ночь.

Г) Некоторые спортсмены являются профессионалами. Иванов спортсмен.

Следовательно, Иванов – профессионал.

Д) В интервале между 24 и 28 не имеется простых чисел.

Е) Алюминий — твердое тело; железо, медь, цинк, серебро, платина, золото, никель, барий, калий, свинец — также твердые тела; следовательно, все металлы— твердые тела.

Ж) Каждое государство имеет свой национальный флаг.

Необходимо заполнить  таблицу (используя буквы, которыми обозначено каждое утверждение) в соответствии с ее указаниями.

 

Ошибочные выводы	Правильные выводы
…	…

2. Связать слова между собой по смыслу, сделать из полученного умозаключение, и определить есть оно правильным или ошибочным.

Дождь, дом, крыша, мокрота

 

Пример:  Золото, ковать, металл.

Связанное: Все металлы куются. Золото – металл.

Вывод: Следовательно, золото куется (ошибочное умозаключение).

3. Переформулируйте утверждение так, чтобы умозаключение из него было правильным?

Некоторые рабочие 2-го управления  —  юристы. Фомин  —  юрист. Следовательно, он работник 2-го управления.

4. Какое из умозаключений является дедукцией?

А) Все арабы смуглы. Ахмед смугл. Следовательно, Ахмед — араб.

Б) Лошади, собаки, куры и коровы смертны.

Лошади, собаки, куры и коровы - животные.

Следовательно, все животные смертны.

В) Петя Смирнов — отличник. Он ученик 9-го класса.

Следовательно, все ученики 9-го класса — отличники.

Г) Иванов герой Советского Союза. Он награжден орденом Ленина. Следовательно, все герои Советского Союза награждены орденом Ленина.

5. Сравните между собой данные выводы (А и  Б). Что можно сказать о каждом из них?

А) Все металлы проводят электричество. Ртуть —  металл.

Следовательно, ртуть проводит электричество.

Б) Ртуть не проводит электричество. Ртуть —  металл.

Следовательно, все металлы не проводят электричество.

6.По данным рисункам сделайте индуктивное и дедуктивное умозаключения.

Рис.1

Рис.2

7. Укажите, в каких случаях умозаключение может быть построено  на основе полной индукции, а в каких – неполной:
а) Все мамонты имеют бивни.
б) Все грибы размножаются спорами.
в) Все ученики нашего класса увлекаются спортом.
г) В интервале между 24 и 28 не имеется простых чисел.
д) Каждое государство имеет свой национальный флаг.

е) Демокрит выдвинул гипотезу об атомистическом строении вещества. Декарт создал аналитическую геометрию. Кант обосновал космогоническую гипотезу о происхождении планет. Лейбниц является основоположником дифференциального и интегрального исчисления.
Демокрит, Декарт, Кант, Лейбниц - философы. Следовательно, все философы внесли значительный вклад в развитие естествознания.

Г.В.Лейбниц     Декарт        Демокрит

ж) Крестьянская война 874 – 901гг в Китае потерпела поражение. Крес­тьянская война 1524 – 1526гг в Германии потерпела поражение. Потерпе­ла поражение крестьянская война в России под предводительством Емель­яна Пугачева в ХVIII в (1773 – 1775гг). Следовательно, все крестьянские войны терпели поражение.

з) При удалении у собаки мозжечка она потеряла способность координировать свои движения. Значит, в этой части мозжечка сосредоточены нервные центры, являющи­еся причиной нормальной координации движений животного.

 д)Разнообразные зеленые растения, помещенные в темноту, утрачивают зеле­ную окраску, будучи пере­несенными на свет, вновь обретают зеленую окраску. Значит, свет и образование зеленой окраски у растений находятся в причинной связи.    

 

Анализируя все это, можно сказать, что индуктивные размышления — один из видов правдоподобных размышлений. Конечно, в каждодневной жизни, размышляя над той или иной проблемой, случайный гражданин врятли будет строить схемы, таблицы, но знание того факта, что свою позицию, точку зрения можно защитить и отстоять в полемике, дискуссии, ссоре, опираясь на научную почву, опираясь на так называемую ”железную” логику, добавит ему уверенности, так как именно знание законов логики, логичных методов, даже хитростей, научит не допускать ошибок в своих рассуждениях и распознавать их в рассуждениях других людей.

http://phenomen.ru/public/dictionary.php?article=1124,

Гайштут. Математика в логических упражнениях.-М:1975

1.2. Связь прошлого с настоящим

Познание окружающего мира человек начинает с изучения единичных вещей, явлений, фактов. Идя от частных случаев, он приходит к общему правилу, от фактов – к обобщению. Никакое теоретическое мышление вообще не было бы возможно, если бы человек индуктивным путем не приходил к установлению тех или иных общих положений. Пока человек не изучил на практике различные металлы, он не знал общего правила, по которому можно определять пригодность того или иного металла, например, для выделки сверла или ножа. Пока человек не познакомился с отдельными жидкостями, он не мог знать такого общего правила, что «все жидкости упруги». Пока человек в процессе трудовой деятельности не начал исследовать отдельные газы, он и представления не имел об общем законе равномерного давления газов на стенки сосудов.

Изучение любых областей внешнего мира человек начинает с исследования единичных предметов, а не с изучения общих положений, общих закономерностей. Это не означает, что из одних общих правил нельзя логически вывести другие общие правила. Это не означает также, что то или иное общее правило нельзя почерпнуть прямо из книги или из беседы с другим человеком. Но при этом одно ясно, что новые общие правила, полученные логическим путем, не могли бы возникнуть, если бы не было тех общих положений, которые легли в основу новых общих правил.

Вы уже имеете начальные сведения об индукции. Индуктивное умозаключение сложилось в процессе многовековой общественно – исторической, производственной практики людей. В течение десятков тысяч лет первобытный человек много раз замечал и фиксировал такие, например, явления природы:

• когда при выделке каменного топора быстро шлифуется один камень о другой, то оба трущиеся камня нагреваются;
• когда при сооружении лодки выскабливается древесина из ствола дерева, то нагревается и дерево и нож;
• если быстро покрутить палку в углублении деревянного бруска, то от получившейся в результате трения теплоты может вспыхнуть сухой трут;
• зимой, когда остынут руки, стоит потереть их друг о друга, как они быстро начинают согреваться и т п.

Так, исследуя явления природы и общества, наблюдая и изучая отдельные предметы, факты и события, люди приходили к общему правилу.  

 В мысли этот процесс познания окружающего мира совершался индуктивно; от единичных суждений человек шёл к общим суждениям, в которых выражалось знание общего правила, общей закономерности. Индуктивная форма умозаключения, являясь отображением производственной практики людей, зародилась вместе с первыми трудовыми навыками людей.

Леонард Эйлер

В  математике уже издавна используется индуктивный метод, основанный  на том, что то или иное общее утверждение делается на основании рассмотрения лишь нескольких частных случаев. История, например, сохранила следующее высказывание Эйлера: «У меня нет для доказательства никаких других доводов, за исключением длинной индукции, которую я провел так далеко, что никоим образом не могу сомневаться в законе, управляющем образованием этих членов…. И кажется невозможным, чтобы закон, который, как было обнаружено, выполняется, например, для 20 членов, нельзя было бы наблюдать и для следующих». Веря в непогрешимость индукции, ученые иногда допускали грубые ошибки. К середине 17 столетия в математике накопилось немало ошибочных выводов. Например, П. Ферма предположил, что все числа вида простые, исходя из того, что при n = 1,2,3,4 они являются таковыми, но

П. Ферма

Л.Эйлер нашел, что уже при n = 5 число 2³²+ 1 = 4294967297 = 641*67004176 не является простым (оно делится на 641). Предположение Ферма было опровержено, среди чисел такого вида встречаются и простые и сложные.

В течение нескольких столетий шла погоня за простыми числами. Многие математики боролись за честь стать открывателем самого большого из известных простых чисел. Числа вида , где p – другое простое число называют простыми числами Марсенна в честь французского монаха Мерена Марсенна (1588-1648), который занимался проблемой совершенных чисел. Если вычислить М =2-1=2047=23*89, то оно тоже непростое.

Известный русский математик Д.О.Граве (1863-1939), сделал предположение, что числа вида , де р – простое число не делится на р.Это предположение верно для всех простых чисел, меньших чем 1000. Через некоторое время было установлено, что при р=1093 число-1 делится на 1093, чем предположение Д.О.Граве было опровержено.

 Стала сильно ощущаться потребность в научно обоснованном методе, который позволял бы делать общие выводы на основании рассмотрения нескольких частных случаев. И такой метод был разработан.

Впервые в чётком изложении метод математической индукции был применён в XVII французским учёным Блезом Паскалем при доказательстве свойств числового треугольника, носящего с того времени его имя. Паскаль Блез (19.6.1623, Клермон-Ферран, — 19.8.1662, Париж),

Блез Паскаль

 

 

Одним из первых, кто начал исследовать индуктивные приемы мышления, был древнегреческий философ Сократ (469 – 399 г. до н. э.) «Знания, - говорил он, - есть понятия об общем, а общее в частных случаях познается путем сравнения этих случаев между собой, т. е., от частного надо идти к общему».

Сократ

Проблемами теории индукции занимался Аристотель (384 – 322 г. до н. э.), выявивший такие виды индукции, как индукция через простое перечисление и неполная индукция. Индукцией особенно заинтересовались в XVII-XVIII вв., когда быстро начали развиваться естественные науки

Аристотель

Однако идея метода математической индукции была известна древним грекам.

Позже эту идею начали называть принципом математической индукции. В частности, в 1838р. в Британской энциклопедии за подписью известного шотландского математика, первого президента Лондонского математического общества Августа де Моргана (1806-1871) была опубликованная статья под названием "Математическая индукция".

Август де Морган

Д. И. Менделеев Д. И. Менделеев, изучив отдельные элементы, открыл периодический закон химических элементов. К. А. Тимирязев, проделав тысячи опытов с многообразными растениями, пришел к выводу, что относительная приспособленность растений выработалась в течение ряда поколений действием естественного и искусственного отбора.

Однако возможность получения с помощью индукции ложного заключения не является основанием для отрицания роли индукции в школьном обучении математике. Во-первых, применение индукции в обучении корректируется и направляется учителем к открытию истин. Во-вторых, нужно добиваться понимания учащимися правдоподобного характера индуктивного заключения. Поэтому, применяя индукцию, необходимо всячески подчеркивать, что заключение является лишь предположением, гипотезой, которое может быть доказано (если оно истинно) или опровергнуто (если оно ложно).

http://phenomen.ru/public/dictionary.php?article=1124

http://works.fio.ru/rsk/r3/4410.htm

1.3.Индукция — как эвристический прием

•                 Индукция в математике. Иногда ученики заявляют, что теорию они знают, все выучили, а вот решать задачи не умеют, не знают, где и когда нужно воспользоваться тем или другим фактом, теоремой, определением, и совсем не представляют себе, с помощью каких соображений удалось открыть ту или иную теорему. Речь идет о том, чтобы ознакомить ученика с простыми общими приема­ми, которые позволяют обнаружить ошибочный ответ при решении той или иной задачи, отбросить собствен­ные ошибочные гипотезы, возникшие у него на различ­ных этапах решения трудной задачи. Наконец, может оказаться, что предложенная ученику задача содержит ошибочное утверждение (к сожалению, такое, тоже случается), в подобной ситуации также важно, чтобы ученик мог быстро установить, не является ли предло­женное утверждение ошибочным.

И наиболее ценным приемом есть индукция.

Индукция — один из самых важных эвристических приемов. Ррассмотрение частных случаев наводит на решение задачи в общем случае. Если задача трудна для нас, то полезно попытаться выделить какой-либо очень простой, ее частный случай, с которым мы в со­стоянии справиться. После этого переходим к другим, более сложным частным случаям, до тех пор пока не доберемся до решения исходной задачи. Особенно полезно в качестве частных случаев брать различные «крайние» случаи. Переход от данной задачи к ее обобщению также нередко позволяет обнаружить способ решения исходной задачи. В самом деле, к более общей задаче могут оказаться применимы методы, ко­торые не применимы к исходной задаче. В частности, к поиску решения более общей задачи можем применить индукцию.

Рассмотрим пример: доказать, что сумма расстояний от любой точки М, лежащей внутри или на контуре правильного треугольника ABC, до его сто­рон есть величина постоянная, не зависящая от положения этой точки..

Способ решения этой задачи легко найти, если последовательно рассмотреть такие случаи: а) точка М — вершина треугольника, тогда ясно, что сумма ее расстояний от сторон треугольника рав­на его высоте; б) точка М — на стороне треугольника (скажем, М — на ВС), этот случай сводится к предыдущему, если через М провес­ти прямую MN || АС, N  положить А' = MN АВ; тогда М — вершина правильного треугольника А'ВМ; в) (общий случай) М— произвольная точка из ∆АВС, этот случай сводится к случаю б), если провести прямую MN || АС, рассмотреть точки A'=MN АВ,   = МN ВС и  ∆ А'ВС'.

Стоит обратить внимание на то, что при решении этой задачи мы вначале (в случаях а и б)  выбирали точку (на  контуре треугольника). Это не случайно. При поиске способа решения задач с помощью индукции особую ценность представляют именно раз­личные «крайние» случаи.

Задачи для самостоятельного решения

1. Пусть фигура Ф — какой-либо параллелограмм, М—его центр симметрии. Пред­ложите способ разбиения фигуры Ф на пять равнове­ликих частей лучами, исходящими из точки М.

Указание

 Вместо исходной зада­чи рассмотрим, более общую: разрезать Ф на а рав­новеликих частей лучами, : исходящими из М. Преимущество новой задачи в том, что к ней применима ин­дукция. Последовательно .рассмотрим задачу для n = 2, 4, 8, 12, 16, для любого п, кратного 4. одновременно, делая: соответствующие рисунки, просматривая которые замечаем, что из решения задачи при n==12 легко получить ее решение и при n= 3 (группируя смежные части, полученные в случае n=12, по четы­ре). После этого ясно, как решить задачу при n=5 и вообще при любом n, не кратном 4.

2.Решите задачу, аналогичную задаче 1, если Ф—треугольник, а М — точка пересечения медиан.

Указание

Легко разрезать  треугольник на 3, 6, 9, 12, 15, 3k равновеликих частей  (к N); затем решим задачу при n = 4 (группируя по три смежные части, полученные при n =12); при n ==5 и вообще при любом п, не кратном 3.

3.На лист  бумаги начерчены  99   кругов,  зануме­рованные числами от   1   до 99. В  каждом круге лежит копеечная   монета.   Кроме   того,   имеются    100   двушек (двухкопеечных  монет),   100   пятаков   и   100   гривенни­ков. Школьник играет с профессором математики и та­кую   игру.   Ход   предоставляется   игрокам   поочередно; при каждом  своем  ходе игрок должен заменить моне­ту,  лежащую в каком-либо  одном   из  кругов,   монетой более высокого достоинства (например,  копейку  можно заменить двушкой, или пятаком,  или гривенником); иг­ра прекращается,  когда  во всех  кругах окажутся  гри­венники;   выигрывает  тот,  кто   произведет   последнюю замену.   Первый   ход  предоставляется   школьнику.  Может ли он так играть, чтобы выиграть  у профессора?

Указание

Вместо данной: задачи рассмотрим ее обобщение, заменив в условии число 99 на n, где п — любое не­четное число. Школьник легко усмотрит выигрыш при n =1 (заменить копейку, на гривенник); при n = 3 (в первой клетке заменить, копейку на гривенник; после какой-либо замены, проведённой профессором в одной из ячеек № 2 и 3, произвести такую же замену в другой из этих ячеек); при п=5. После этого ясна выигрышная стратегия школьника: первым ходом поло­жить в какую-нибудь ячейку гривенник вместо копей­ки;  после каждой, замены, произведенной  профессором в какой-либо   ячейке,  произнести  такую   же  замену в другой  ячейке   (ясно,  что  у  школьника    всегда  такая возможность  будет,   ибо  после  каждого  его  хода  чис­ло  ячеек, в которых одинаковые монеты,  четно).

 

•                 Индукция при поиске математических закономерностей Рас­сматривая какой-либо класс геометрических фигур, иногда удает­ся подметить, что некоторые частные виды этих фигур обладают од­ним и тем же общим свойством. Это может нас навести на мысль, что все фигуры рассматриваемого класса обладают тем же свойством. Например, рассматривая правильный треугольник, равнобедрен­ный треугольник, прямоугольный треугольник, можно подметить, что в каждом из них любая из медиан меньше суммы двух других медиан. Это нас наталкивает на мысль, что в любом треугольнике любая из медиан меньше суммы двух других его медиан.

Следует, однако, иметь в виду, что в результате рассмотрения частных случаев мы можем прийти только к некоторой гипотезе, к некоторому предположению. Не исключено, что эта гипотеза ока­жется ложной, даже если рассмотрено очень большое число част­ных  случаев,

Приведем пример. Обозначим через S_n наибольшее число об­ластей, на которые можно разбить плоскость n окружностями.

Легко проверить, что S₁= 2,   S₂ = 4, S₃= 8.

Возникает предположение, что при любом натуральном n будет S_n = 2ⁿ. Однако можно показать, что это заключение ошибочно, например S₄ = 14, а не 16. Предположение, полученное из индуктивных соображений, нуж­дается еще в доказательстве. Прежде всего, необходимо научиться формулировать математические предположения на основании наб­людений, проведенных в ряде частных случаев, а затем уже выяс­нять, будут ли полученные гипотезы истинными или ложными.     

Балк М.Б., Балк Г.Д. Математика после уроков

2.Метод математической индукции

2.1.Принцип математической индукции

Как мы уже отмечали, мышление по индукции в одних случаях может привести к правильным общим утверждениям, в других – к неправильным. Тоесть возникает потребность в методе, который бы добавил возможность определить, в каких случаях гипотеза верна, а в каких – нет. Таким методом есть так называемый метод математической индукции.

Метод математической индукции можно сравнить с прогрессом. Мы начинаем с низшего, в результате логического мышления приходим к высшему. Человек всегда стремился к прогрессу, к умению развивать свою мысль логически, а значит, сама природа предначертала ему размышлять индуктивно. А ведь это так важно – уметь размышлять индуктивно!

   Именно поэтому, проводятся различные  эвристические межшкольные занятия, где помогают учащимся научиться размышлять индуктивно, используя при решении задач метод математической индукции, сформировать у них умения и навыки по применению этого метода на практике к решению самых разнообразных задач.

Пример 1.Верно ли числовое равенство

1²+2²+ … +100² =

Указание

Вместо данного нужно доказать более общее равенство:

1²+2²+ … + п ² = .

Доказательство проводится с помощью  метода  математической ин­дукции.

 

Пример 2. (из физики). В учебнике «Физика 9» выражение    для перемещения тела (материальной точки) при прямолинейном равноускоренном движении выводится из графика зависимости скорости от времени. Но это же выражение можно получить и прямым вычислением, используя метод математической индукции. Покажем это.

    Пусть тело движется прямолинейно, но не равномерно, а с постоянным ускорением a в течение времени  t , начиная с некоторого начального момента  t=0, когда начальная скорость равна  . Разделим мысленно всё время движения на одинаково малые промежутки времени настолько малое, что среднюю скорость в течение времени можно считать постоянной, но концу промежутка скорость как бы скачком возрастает на величину a.

  За промежуток перемещение

Для первого промежутка ==+=

(+)=

 Для второго промежутка.

      

Аналогично для третьего.

и т.д., выведем формулу для n-го промежутка S.

.

,

Сумма нечётных чисел натурального ряда равна n

1+3+5+…+2n-1=n

Тогда Но а и окончательно

.

Принцип математической индукции является одной из аксиом множества натуральных чисел, имеющей много применений в математике, и потому не доказывается. На этом принципе основан метод доказательства, называемый методом математической индукции.

Часто индукцию сравнивают с падением ряда доминошек: мы толкаем первую доминошку - она падает и задевает вторую. Вторая доминошка от этого тоже падает и задевает третью. Теперь падает третья доминошка, задевает четвертую…- и в итоге падает весь ряд. А происходит это по двум причинам: 1)мы толкаем первую доминошку; 2)любая доминошка, падая, задевает следующую.

Метод математической индукции можно применять только для доказательства утверждений, зависящих от натурального n. Метод математической индукции позволяет в поисках общего закона испытывать возникающие при этом гипотезы, отбрасывать ложные и утверждать истинные.

Он широко применяется при доказательстве теорем, тождеств, неравенств, при решении задач на делимость, при решении некоторых геометрических и многих других задач.

В основном он применяется для решения задач двух видов:

1) исходя из частных наблюдений устанавливают некоторую закономерность и затем доказывают её справедливость методом математической индукции;

2) доказывают справедливость некоторой формулы методом математической индукции.

 Полная индукция имеет в математике лишь ограниченное применение. Многие интересные математические утверждения охватывают бесконечное число частных случаев, а провести проверку для бесконечного числа случаев человек не может (примером такого утверждения может служить любое утвер­ждение, относящееся ко всем натуральным числам). Неполная же индукция, как мы уже видели раньше, часто приводит к ошибочным результатам. Во многих случаях выход из такого рода затруднений заключается в обращении к методу математической индукции. Этот метод доказательства – это утверждение типа: «Для каждого натурального n верно, что ...». Такое утверждение можно рас­сматривать как цепочку утверждений: «Для n = 1 верно, что ...», «Для n = 2 верно, что...» и т.д.

Первое утверждение цепочки называется базой (или основанием) индукции. Его обычно легко проверить. Затем доказывается индуктивный переход (или шаг индукции): «Если верно утверждение с номером n, то верно утверждение с номером (n + 1)». Индуктивный переход также можно рассматривать как це­почку переходов: «Если верно утверждение 1, то верно утверждение 2», «Если верно утверждение 2, то верно утверждение 3» и т.д.

Если верна база индукции и верен индуктивный переход, то все утвержде­ния верны (это принцип математической индукции).

Иногда для доказательства очередного утверждения цепочки надо опираться на все предыдущие утверждения. Тогда индуктивный переход звучит так: «Если верны все утверждения с номерами от 1 до n, то верно утверждение с номером (n + 1)».

Иногда удобен индуктивный спуск — если утверждение с номером n (n > 1) можно свести к одному или нескольким утверждениям с меньшими номерами и первое утверждение верно, то все утверждения верны.

Роль аксиомы математической индукции состоит именно в том, что она позволяет заменить бесконечное индуктивное рассуждение конечным дедуктивным.

Пример 3. Признак перпендикулярности прямой и плоскости - известная теорема стереометрии. Можно сообщить учащимся формулировку теоремы, изложить ее доказательство. Этот подход малоэффективен.

Можно поступить иначе. Определение перпендикулярности прямой к плоскости неэффективно: мы не можем проверить перпендикулярность данной прямой к любой прямой плоскости, таких прямых бесконечно много. Возникает задача: нельзя ли указать некоторое достаточное условие перпендикулярности прямой к любой прямой плоскости?

Возникает гипотеза: перпендикулярность к одной прямой плоскости. Но она быстро опровергается, можно построить модель прямой, перпендикулярной к одной прямой плоскости, но не перпендикулярной к другой.

Возникает другая гипотеза: перпендикулярность к двум прямым плоскости. Это уже кажется более правдоподобно (пока все учащиеся берут две пересекающиеся прямые плоскости). Однако и здесь обнаруживается противоречащий случай (если взять параллельные прямые плоскости, можно указать прямую, перпендикулярную им, но не перпендикулярную некоторой третьей прямой плоскости).

Наконец, формулируется уточненная гипотеза: если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна любой прямой плоскости, т. е. и самой плоскости. Таким путем мы открываем то, что подлежит дедуктивному доказательству.

Приведенный пример относится к курсу 9 класса. Он подтверждает, что и на этом этапе обучения индуктивного метода не теряет своего значения.

Выше сказанное сформулируем в общий принцип.

П р и н ц и п  м а т е м а т и ч е с к о й  и н д у к ц и и. Если предложение А (n), зависящее от натурального числа n, истинно для n=1 из того, что оно истинно для n=k (где k - любое натуральное число), следует, что оно истинно и для следующего числа n=k+1, то предложение А (n) истинно для любого натурального числа n.

Занимательно и доступно это можно сформулировать так: «Пусть в очереди первой стоит женщина, и за каждой женщиной пусть стоит женщина. Тогда все в очереди - женщины!»­ - вот шутливая формулировка прин­ципа математической индукции. А вот серьезная: «Пусть имеется последо­вательность утверждений У, У, У, ... Пусть первое утверждение У верно, и пусть за каждым верным утверждением Устоит верное утверж­дение У.Тогда все утвержде­ния У верны». Ну, что ж. Это действительно так. Поскольку за каждым верным утверж­дением У следует верное утвержде­ние У поскольку утверждение У верно, то утверждение У верно; а раз Уверно, то и У верно; но тогда и У, следующее за У, вер­но, и т. д.

Рассмотрим на примерах

1. Докажите, что если плоскость разбита на части прямыми и окружностями, то получившуюся карту можно раскрасить в два цвета так, что части, граничащие по дуге или отрезку, будут разного цвета.

Решение.

Доказательство проведем индукцией по общему числу прямых и окружностей. Для одной прямой или окружности утверждение очевидно. Предположим теперь, что можно раскрасить требуемым образом любую карту, заданную n прямыми и окружностями, и покажем, как тогда раскрасить карту, заданную n + 1 прямыми и окружностями. Выбросим одну из этих прямых (или окружностей) и раскрасим карту, заданную оставшимися n прямыми и окружностями. Затем цвета всех частей, лежащих по одну сторону от выброшенной прямой (или окружности), сохраним, а цвета всех частей, лежащих по другую сторону, заменим на противоположные.

2. Докажите, что в выпуклом n-угольнике нельзя выбрать больше n диагоналей так, чтобы любые две из них имели общую точку.

Решение.

Докажем индукцией по n, что в выпуклом n-угольнике нельзя выбрать более n сторон или диагоналей так, чтобы любые две из них имели общую точку. При n = 3 это очевидно. Предположим, что утверждение верно для любого выпуклого n-угольника, и докажем его для (n + 1)-угольника. Если из каждой вершины (n + 1)-угольника выходит не более двух выбранных сторон или диагоналей, то их всего выбрано не более n + 1. Поэтому будем считать, что из некоторой вершины A выходят три выбранные стороны или диагонали AB₁, AB₂ и AB₃, причем AB₂ лежит между AB₁ и AB₃. Так как диагональ или сторона, выходящая из точки B₂ и отличная от AB₂ не может одновременно пересекать AB₁ и AB₃, то из B₂ выходит только одна выбранная диагональ. Поэтому можно выбросить точку B₂ вместе с диагональю AB₂ и применить предположение индукции.

3. Пусть E - точка пересечения боковых сторон AD и BC трапеции ABCD, B_n + 1 - точка пересечения прямых A_nC и BD (A₀ = A), A_n + 1 - точка пересечения прямых EB_n + 1 и AB. Докажите, что A_nB = AB/(n + 1).

Решение.

 Ясно, что A₀B = AB. Пусть C_n - точка пересечения прямых EA_n и DC, DC : AB = k, AB = a, A_nB = a_n и A_n + 1B = x. Так как CC_n + 1 : A_nA_n + 1 = DC_n + 1 : BA_n + 1, то kx : (a_n – x) = (ka – kx) : x, т. е. x = aa_n/(a + a_n). Если a_n = a/(n + 1), то x = a/(n + 2).

4. Докажите, что если n точек не лежат на одной прямой, то среди прямых, их соединяющих, не менее n различных.

Решение .

Доказательство проведем индукцией по n. При n = 3 утверждение очевидно. Предположим, что мы доказали его для n – 1 точки и докажем его для n точек. Если на каждой прямой, проходящей через две данные точки, лежит еще одна данная точка, то все данные точки лежат на одной прямой (см. задачу 20.13). Поэтому существует прямая, на которой лежат ровно две данные точки A и B. Выбросим точку A. Возможны два случая.

1. Все оставшиеся точки лежат на одной прямой l. Тогда будет ровно n различных прямых: n – 1 прямая, проходящая через A, и прямая l.

2. Оставшиеся точки не лежат на одной прямой. Тогда среди прямых, их соединяющих, по предположению индукции есть не менее n – 1 различных, причем все они отличны от прямой l. Вместе с прямой AB они составляют не менее n прямых.

Метод математической индукции широко применяется при доказательстве теорем, тождеств, неравенств, при решении задач на делимость, при решении некоторых геометрических и многих других задач. Рассмотрим каждый из них отдельно.

2.2. Применение метода математической индукции для доказательства справедливости тождеств

1.Доказать, что при любом n справедливо утверждение: 1²+2²+3²+…+n²=n(n+1)(2n+1)/6.

 

Решение: 1) Пусть n=1, тогда Х₁=1²=1(1+1)(2+1)/6=1.

Значит, при n=1 утверждение верно. 2) Предположим, что n=k Х_k=k²=k(k+1)(2k+1)/6.

3) Рассмотрим данное утверждение при n=k+1 X_k+1=(k+1)(k+2)(2k+3)/6.

X_k+1=1²+2²+3²+…+k²+(k+1)²=k(k+1)(2k+1)/6+ (k+1)²=(k(k+1)(2k+1)+6(k+1)²)/6=(k+1)(k(2k+1)+

+6(k+1))/6=(k+1)(2k²+7k+6)/6=(k+1)(2(k+3/2)(k+2))/6=(k+1)(k+2)(2k+3)/6.

Мы доказали справедливость равенства и при n=k+1, следовательно, в силу принципа математической индукции, утверждение верно для любого натурального n.

2. Доказать, что  1+х+х²+х³+…+хⁿ=(хⁿ⁺¹-1)/(х-1), где х1.

Решение: 1) При n=1 получаем  1+х=(х²-1)/(х-1)=(х-1)(х+1)/(х-1)=х+1

следовательно, при n=1 формула верна; А(1) истинно.

2) Пусть k-любое натуральное число и пусть формула верна при n=k, т.е. 1+х+х²+х³+…+х^k=(х^k+1-1)/(х-1). Докажем, что тогда выполняется равенство 1+х+х²+х³+…+х^k+x^k+1=(x^k+2-1)/(х-1). В самом деле

1+х+х²+x³+…+х^k+x^k+1=(1+x+x²+x³+…+x^k)+x^k+1=(x^k+1-1)/(x-1)+x^k+1=

=(x^k+2-1)/(x-1).

Итак, А(k)A(k+1). На основании принципа математической индукции заключаем, что формула верна для любого натурального числа n.

3.Доказать верность тождества (1²/13)+(2²/35)+…+(n²/(2n-1)(2n+1))=n(n+1)/2(2n+1) для любого натурального n.

Решение: 1) При n=1 тождество верно 1²/13=1(1+1)/2(2+1). 2) Предположим, что при n=k

(1²/13)+…+(k²/(2k-1)(2k+1))=k(k+1)/2(2k+1).  3) Докажем, что тождество верно при n=k+1.

(1²/13)+…+(k²/(2k-1)(2k+1))+(k+1)²/(2k+1)(2k+3)= (k(k+1)/2(2k+1))+((k+1)²/(2k+1)(2k+3))= =((k+1)/(2k+1))((k/2)+((k+1)/(2k+3)))=(k+1)(k+2)(2k+1)/2(2k+1)(2k+3)=(k+1)(k+2)/2(2(k+1)+1).

 Следовательно, в силу принципа математической индукции, тождество верно для любого натурального n.

4. Доказать тождество: n!+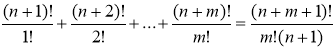

Решение: Проверим справедливость для m=1.

S(m=1)=n!+(n+1)!=n!+n!(n+1)=n!(1+n+1)=n!(n+2)

S(m=1)=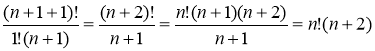

Для m=1 формула верна. Предположим, что она верна для какого-либо натурального m=k, т.е S(k)=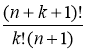. Докажем, что она будет верна и дляm=k+1, т.е.

S(k+1)=k!+.

S(k+1)=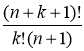

Мы получили ту же формулу, т.е. мы доказали, что формула верна и для m=k+1.Следовательно, в силу принципа математической индукции данная формула верна для любого натурального n.

 

 

Задачи для самостоятельного решения

на доказательство равенств

Доказать тождества.

1.1³+2³+3³+…+n³=.                                                                                                                  

2. **…=,если n ≥2

 

3.   +-+…+(-1)=)

 4.  

(Ответы см. в приложении (А))

2.3.Применение метода математической индукции для вывода некоторых математических закономерностей и доказательства их справедливости

 

1.Доказать методом математической индукции формулу общего члена

суммы первых n членов геометрической прогрессии:

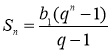, при

Решение: 1) При n=1 формула верна: .2) Предположим, что формула верна для n=k и исходя из предположения докажем её справедливость для n=k+1. Из утверждения: , поэтому . То есть . Вывод: формула общего члена геометрической прогрессии верна для любого натурального числа n.

2.Доказать самостоятельно правильность формулы 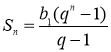суммы первых n членов геометрической прогрессии.

Решение: При n=1 формула верна  , . Предположим, что формула верна для n=k,  .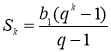

Для n=k+1 формула будет иметь вид . Действительно

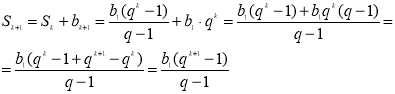
Что и нужно было доказать. То есть формула суммы n первых членов геометрической прогрессии верна для любого натурального n , .

3.Найти сумму ряда S(n)=.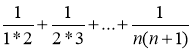

 

Решение: S(1)=,  S(2)=,

S(3)= . Рассматривая эти суммы видим, что в числителе стоит n,а в знаменателе ,т.е. знаем.n-го слагаемого ,тогда предположим, что S(n)=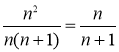, т.е. 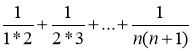=. Проверим справедливость для n=1

, S(1)=. Верно. Предположим, что она верна для какого-либо натурального n=k, т.е. S(k)=. Докажем, что она будет верна и для n=k+1, т.е. S(k+1)=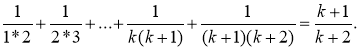

Мы получили ту же формулу, т.е. мы доказали, что формула верна и для n=k+1.Следовательно, в силу принципа математической индукции данная формула верна для любого  натурального n.

Значит по формуле S(n)= можно получать сумму любых n слагаемых в последовательности.

4. Найти сумму ряда 1*1!+2*2!+3*3!+…+n*n!

Решение: S(1)=1*1!=1*1=1, S(2)=1*1!+2*2!=1*1+2*1*2=5,

S(3)=1*1!+2*2!+3*3!=1*1+2*1*2+3*1*2*3=23. Можно заметить, что S(n)=(n+1)-1. S(1)=1. Проверим справедливость для n=1.

S(1)=(1+1)!-1=2!-1=1*2-1. – верно. Предположим, что она верна для какого-либо натурального n=k, т.е. S(k)=(k+1)!-1. Докажем, что она будет верна и для n=k+1, т.е.S(k+1)=S(k)+(k+1)(k+1)!=(k+1)!-1+(k+1)(k+1)!=(k+1)!(k+1)-1=(k+1)!(k+2)-1=(k+2)!-1. Мы получили ту же формулу, т.е. мы доказали, что формула верна и для n=k+1.Следовательно, в силу принципа математической индукции данная формула верна для любого натурального n. Значит по формуле S(n)= (n+1)!-1 можно получать сумму любых n слагаемых в последовательности.

5. Найти сумму ряда …+

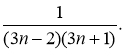
Решение: S(1)=, S(2)= =, S(3)=

Можно заметить, что S(n)=. Проверим справедливость для n=1.

S(1)=, S(1)= – верно. Предположим, что она верна для какого-либо натурального n=k, т.е. S(k)= Докажем, что она будет верна и для n=k+1, т.е.

S(k+1)=…+.

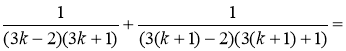
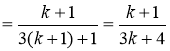S(k+1)=S(k)+=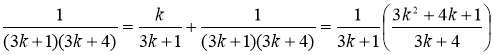

=

Мы получили ту же формулу, т.е. мы доказали, что формула верна и для n=k+1.Следовательно, в силу принципа математической индукции данная формула верна для любого  натурального n. Значит по формуле S(n)= можно получать сумму любых n слагаемых в последовательности.

 

Задачи для самостоятельного решения

на доказательство равенств

1. Докажите, что сумма членов каждой строки таблицы

1

2,3,4

3,4,5,6,7

равна квадрату нечетного числа, порядковый номер которого равен номеру строки от начала таблицы. S(n)=.

(Ответы см. в приложении (В))

2.4.Решение неравенств с помощью метода

математической индукции

1.Доказать, что если n>2 и х>0, то справедливо неравенство  (1+х)ⁿ>1+nх (неравенство Бернулли).

Решение: 1) При n=2 неравенство справедливо, так как (1+х)²=1+2х+х²>1+2х. Значит, А(2) истинно.

2) Докажем, что А(k)A(k+1), если k> 2. Предположим, что А(k) истинно, т.е., что справедливо неравенство (1+х)^k>1+kx.

3) Докажем, что тогда и А(k+1) истинно, т.е., что справедливо неравенство (1+x)^k+1>1+(k+1)x. В самом деле, умножив обе части неравенства (3) на положительное число 1+х, получим (1+x)^k+1>(1+kx)(1+x). Рассмотрим правую часть последнего неравенства, имеем

(1+kx)(1+x)=1+(k+1)x+kx²>1+(k+1)x. В итоге получаем, что (1+х)^k+1>1+(k+1)x.

Итак, А(k)A(k+1). На основании принципа математической индукции можно утверждать, что неравенство Бернулли справедливо для любого n> 2.

2.Доказать, что при n>2 справедливо неравенство 1+(1/2²)+(1/3²)+…+(1/n²)<1,7-(1/n).

Решение: При n=3 неравенство верно 1+(1/2²)+(1/3²)=245/180<246/180= =1,7(1/3). Предположим, что при n=k 1+(1/2²)+(1/3²)+…+(1/k²)=1,7-(1/k).

Докажем справедливость неравенства при n=k+1 (1+(1/2²)+…+(1/k²))+(1/(k+1)²)<1,7-(1/k)+(1/(k+1)²). Докажем, что 1,7-(1/k)+(1/(k+1)²)<1,7-(1/k+1)(1/(k+1)²)+(1/k+1)<1/k(k+2)/(k+1)²<1/k

 k(k+2)<(k+1)²k²+2k<k²+2k+1. Последнее очевидно, а поэтому 1+(1/2²)+(1/3²)+…+(1/(k+1)²)<1,7-(1/k+1).

Следовательно, в силу принципа математической индукции, тождество верно для любого натурального n.

3. Доказать, что для произвольного n N  .

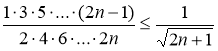Решение: 1) При n=1 утверждение верно: 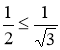; Покажем, что из истинности неравенства Т следует истинность утверждения Т, то есть следует верно неравенство: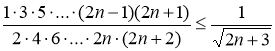. Оценим левую часть этого неравенства, имеем:

.

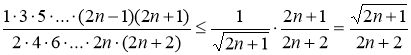Очевидно, что для истинности утверждения Т достаточно, чтобы имело справедливость неравенство 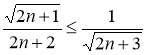, что равносильно очевидному

неравенству . В силу принципа математической индукции неравенство для всех n N.

4.Докажем следующее утверждение: . Как один из вариантов доказательства, воспользуемся методом математической индукции.

Решение: Для утверждение верно, пусть тогда тоже верно, тогда

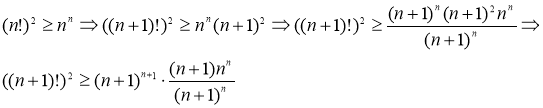
Отсюда видно, что если удастся доказать, ч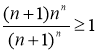то , то будет тем более верно. 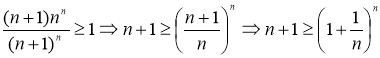, как видно правая часть неравенства стремится к числу , а следовательно не превышает 3, таким образом достаточно проверить это неравенство для , чтобы убедиться в его истинности. Как показывает проверка, неравенство верно, а значит, выполняется необходимое нам неравенство . Базис индукции верен, как и индукционный переход, значит по принципу математической индукции наше утверждение, что верно.

Задачи для самостоятельного решения.

1. Докажите, что при любом натуральном n>3 справедливо неравенство.

+….

 

2. Докажите, что 2 >(n+1) при n ≥ 3.

 

3.  Докажите, что при любом натуральном n≥ 2 справедливо неравенство

(Ответы см. в приложении (С))

2.5.Делимость чисел и метод математической индукции

1.Доказать, что (11ⁿ⁺²+12²ⁿ⁺¹) делится на 133 без остатка.

Решение: 1) Пусть n=1, тогда 11³+12³=(11+12)(11²-132+12²)=23133.

Но (23133) делится на 133 без остатка, значит при n=1 утверждение верно; А(1) истинно.

2) Предположим, что (11^k+2+12^2k+1) делится на 133 без остатка.

3) Докажем, что в таком случае (11^k+3+12^2k+3) делится на 133 без остатка. В самом деле 11^k+3+12^2л+3=1111^k+2+12²12^2k+1=1111^k+2+(11+133)12^2k+1=11(11^k+2+12^2k+1)+13312^2k+1. Полученная сумма делится на 133 без остатка, так как первое её слагаемое делится на 133 без остатка по предположению, а во втором одним из множителей выступает 133. Итак, А(k)А(k+1). В силу принципа математической индукции утверждение доказано.

2.Доказать, что при любом n 7ⁿ-1 делится на 6 без остатка.

Решение: 1) Пусть n=1, тогда Х₁=7¹-1=6 делится на 6 без остатка. Значит при n=1утверждение верно. 2) Предположим, что при n=k7^k-1 делится на 6 без остатка.

3) Докажем, что утверждение справедливо для n=k+1. X_k+1=7^k+1-1=77^k-7+6=7(7^k-1)+6. Первое слагаемое делится на 6, поскольку 7^k-1 делится на 6 по предположению, а вторым слагаемым является 6. Значит 7ⁿ-1 кратно 6 при любом натуральном n. В силу принципа математической индукции утверждение доказано.

3.Доказать, что 3^3n-1+2^4n-3 при произвольном натуральном n делится на 11.

Решение: 1) Пусть n=1, тогдаХ₁=3^3-1+2^4-3=3²+2¹=11 делится на 11 без остатка. Значит, при n=1 утверждение верно.2) Предположим, что при n=k X_k=3^3k-1+2^4k-3 делится на 11 без остатка.3) Докажем, что утверждение верно для n=k+1.

X_k+1=3^3(k+1)-1+2^4(k+1)-3=3^3k+2+2^4k+1=3³3^3k-1+2⁴2^4k-3=273^3k-1+162^4k-3= (16+11)3^3k-1+162^4k-3= =163^3k-1+113^3k-1+162^4k-3=16(3^3k-1+2^4k-3)+113^3k-1.

Первое слагаемое делится на 11 без остатка, поскольку 3^3k-1+2^4k-3 делится на 11 по предположению, второе делится на 11, потому что одним из его множителей есть число 11. Значит и сумма делится на 11 без остатка при любом натуральном n. В силу принципа математической индукции утверждение доказано.

4.Доказать, что 11²ⁿ-1 при произвольном натуральном n делится на 6 без остатка.

Решение: 1) Пусть n=1, тогда 11²-1=120 делится на 6 без остатка. Значит при n=1 утверждение верно. 2) Предположим, что при n=k  11^2k-1 делится на 6 без остатка.

3) Докажем, что утверждение верно при n=k+1

11^2(k+1)-1=12111^2k-1=12011^2k+(11^2k-1).

Оба слагаемых делятся на 6 без остатка: первое содержит кратное 6 число 120, а второе делится на 6 без остатка по предположению. Значит и сумма делится на 6 без остатка. В силу принципа математической индукции утверждение доказано.

5.Доказать, что 3³ⁿ⁺³-26n-27 при произвольном натуральном n делится на 26²(или 676) без остатка.

Решение: Предварительно докажем, что 3³ⁿ⁺³-1 делится на 26 без остатка. При n=0 3³-1=26 делится на 26. Предположим, что при n=k 3^3k+3-1 делится на 26. Докажем, что утверждение верно при n=k+1. 3^3k+6-1=273^3k+3-1=263^3л+3+(3^3k+3-1) –делится на 26. Теперь проведём доказательство утверждения, сформулированного в условии задачи. 1) Очевидно, что при n=1 утверждение верно 3³⁺³-26-27=676.  2) Предположим, что при n=k выражение 3^3k+3-26k-27 делится на 26² без остатка. 3) Докажем, что утверждение верно при n=k+1  3^3k+6-26(k+1)-27=26(3^3k+3-1)+(3^3k+3-26k-27).

Оба слагаемых делятся на 26²; первое делится на 26², потому что мы доказали делимость на 26 выражения, стоящего в скобках, а второе делится по предположению индукции. В силу принципа математической индукции утверждение доказано.

Задачи для самостоятельного решения

1. Доказать, что при любом натуральном n имеем: кратно 16.

2.Доказать, что при произвольном k значение k- k делится на 30.

(Ответы см. в приложении  (D))

2.6.Применение метода математической индукции

для решения геометрических задач

1.Доказать, что число диагоналей выпуклогоn-угольника равно n(n-3)/2.

Решение: 1) При n=3 утверждение справедливо, ибо в треугольнике ₃=3(3-3)/2=0 диагоналей; А(3) истинно. 2) Предположим, что во всяком выпуклом k-угольнике имеется _k=k(k-3)/2 диагоналей. Докажем, что тогда в выпуклом (k+1)-угольнике число диагоналей _k+1=(k+1)(k-2)/2.

Пусть А₁А₂А₃…A_kA_k+1-выпуклый (k+1)-угольник. Проведём в нём диагональ A₁A_k. Чтобы подсчитать общее число диагоналей этого (k+1)-угольника  нужно  подсчитать  число  диагоналей  в  k-угольнике A₁A₂…A_k, прибавить к полученному числу k-2, т.е. число диагоналей (k+1)-угольника, исходящих из вершины А_k+1, и, кроме того, следует учесть диагональ А₁А_k. Таким образом, _k+1=_k+(k-2)+1=k(k-3)/2+k-1=(k+1)(k-2)/2. Итак, А(k)A(k+1). Вследствие принципа математической индукции утверждение верно для любого выпуклого n-угольника.

2.Докажите, что в выпуклом n-угольнике нельзя выбрать больше n диагоналей так, чтобы любые две из них имели общую точку.

Решение: Докажем индукцией по n, что в выпуклом n-угольнике нельзя выбрать более n сторон или диагоналей так, чтобы любые две из них имели общую точку. При n = 3 это очевидно. Предположим, что утверждение верно для любого выпуклого n-угольника, и докажем его для (n + 1)-угольника. Если из каждой вершины (n + 1)-угольника выходит не более двух выбранных сторон или диагоналей, то их всего выбрано не более n + 1. Поэтому будем считать, что из некоторой вершины A выходят три выбранные стороны или диагонали AB₁, AB₂ и AB₃, причем AB₂ лежит между AB₁ и AB₃. Так как диагональ или сторона, выходящая из точки B₂ и отличная от AB₂ не может одновременно пересекать AB₁ и AB₃, то из B₂ выходит только одна выбранная диагональ. Поэтому можно выбросить точку B₂ вместе с диагональю AB₂ и применить предположение индукции.

3.Пусть E – точка пересечения боковых сторон AD и BC трапеции ABCD, B_n + 1 – точка пересечения прямых A_nC и BD (A₀ = A), A_n + 1 – точка пересечения прямых EB_n + 1 и AB. Докажите, что A_nB = AB/(n + 1).

Решение: Ясно, что A₀B = AB. Пусть C_n – точка пересечения прямых EA_n и DC, DC : AB = k, AB = a, A_nB = a_n и A_n + 1B = x. Так как CC_n + 1 : A_nA_n + 1 = DC_n + 1 : BA_n + 1, то kx : (a_n – x) = (ka – kx) : x, т. е. x = aa_n/(a + a_n). Если a_n = a/(n + 1), то x = a/(n + 2).

4.Докажите, что если n точек не лежат на одной прямой, то среди прямых, их соединяющих, не менее n различных.

Решение: Доказательство проведем индукцией по n. При n = 3 утверждение очевидно. Предположим, что мы доказали его для n – 1 точки и докажем его для n точек. Если на каждой прямой, проходящей через две данные точки, лежит еще одна данная точка, то все данные точки лежат на одной прямой (см. задачу 20.13). Поэтому существует прямая, на которой лежат ровно две данные точки A и B. Выбросим точку A. Возможны два случая.

1. Все оставшиеся точки лежат на одной прямой l. Тогда будет ровно n различных прямых: n –1 прямая, проходящая через A, и прямая l.

2. Оставшиеся точки не лежат на одной прямой. Тогда среди прямых, их соединяющих, по предположению индукции есть не менее n – 1 различных, причем все они отличны от прямой l. Вместе с прямой AB они составляют не менее n прямых.

Задачи для самостоятельного решения

1. Докажите, что n прямых, расположенных в одной плоскости, из которых

никакие две не параллельны и никакие три не проходят через одну точку, делят плоскость на частей.

2. Докажите, что n плоскостей делят пространство на при условии, что никакие две из этих плоскостей не параллельны, никакие три не проходят через одну прямую, никакие четыре – через одну точку и никакие две линии пересечения данных плоскостей не параллельны.

3.Докажите, что n окружностей, расположенных на одной плоскости, делят  плоскость не более чем на n-n+2 частей.

(Ответы см. в приложении  (I))

2.7.Занимательные задачи на индукцию

Задача 1.

Пользуясь методом математической индукции, мы сейчас докажем явно нелепое утверждение: ”Все мальчики одного роста”.Это удастся потому, что в ходе доказательства мы сознательно допустим ошибку. Найдите то место в рассуждении, где эта ошибка допущена.

Итак, мы беремся доказать следующее: при любом натуральном n любые n мальчиков имеют одинаковый рост.

Доказательство. При n=1 теорема, очевидно, верна. Пусть она верна при n=k (то есть любых к мальчиков одинакового роста). Действительно, занумеруем мальчиков в каком-либо порядке числами 1, 2, 3, …, k, k+1. По индуктивному допущению мальчики с номерами от 1 до k имеют один и тот же рост – такой же, как у “мальчика номер k”.

С другой стороны, k мальчиков с номерами 2, 3, 4, …, k, k+1 также имеют один и тот же рост (в силу того же допущения), опять-таки такой же как у мальчика номер k. Следовательно, все k+1 мальчиков имеют один рост.

Итак, теорема проверена при  n=1, и  из ее справедливости при n= k мы вывели ее справедливость при п= k+1. Следовательно, теорема верна для всех натуральных п. В чем ошибка?

Задача 2.«Фокус-покус»

                                                             «Если на клетке слона написано «буйвол»- не верь глазам своим».

 Кузьма Прутков.

Афоризм с помощью метода математической индукции можно обосновать следующий поразительный фокус. Вырежьте из картона 999 оди­наковых карточек. На 111 карточках напишите 1, на 111 карточках-2, и т.д. - на последних 111 карточ­ках напишите 9. Переверните все карточки цифрой вниз и тщательно перемешайте. Затем возьмите совер­шенно произвольно п карточек, где п - любое целое число от 1 до 100, и положите их на стол цифрой вверх. Тогда цифры, написанные на всех n выбранных карточках, обязательно окажутся одинаковыми! Сколько бы раз ни повторять этот фокус и какое бы п ни выбирать(), результат неизменно будет один: на всех п карточках будет одна и та же цифра! Каждый может на досуге проверить сказанное экспериментально, а сейчас докажем этот замечательный факт по индукции.

Нам нужно доказать утвержде­ние У: на всех п выбранных карточках (), окажется одна и та же цифра. Фактически здесь имеется 100 утверждений: У,..., У(в зависимости от того, какое значение принимает n).   При п = 1 наше утверждение, очевидно, справедливо. (В этом нет, правда, ничего удивительного: если цифрой вверх будет перевернута всего одна карточка, то, разумеется, перед нами окажется одна цифра). Докажем теперь, что если утверж­дение Уверно при п =k (где k ­любое целое число от 1 до 99), то оно верно и при п = k + 1. Положим на стол цифрой вверх k + 1 карточку. Одну карточку (на­зовем ее А) на минутку снимем со стола. На столе останется k карточек.  На них (по предположению индук­ции) написана одна и та же цифра (некоторая цифра, X). Итак, на всех карточках - кроме, быть может, А - написана цифра Х. Заменим теперь одну из k карточек на столе карточкой А. На столе по-прежнему k карточек, значит, по предположению индукции, на них всех написана одна и та же цифра (которую мы выше обозначили через Х). В том числе цифра Х написана и на кар­точке А, которую мы вначале сняли, а теперь вернули на стол. Итак, на карточке А  тоже написа­на цифра Х. Значит, на всех п карточках (п = k + 1) написана цифра Х, что и требовалось доказать.

Таким образом, в задаче  1 утверждение У верно, и за каждым верным утверждением У () следует верное утверждение У Следовательно, все утверждения У верны (). И как ни порази­телен наш фокус с карточками, он теперь обязан всегда получаться­ – это строго доказано!

Найдите ошибку в рассуждении.

Задача 3 .«На пальцах»

                                                                  «Из мешка вывалился большой ,

                                                         крайне рассерженный двупалый ленивец».

                                                           Дж. Даррелл. Три билета до Эдвенчер.

Рассуждая так же, как и в задаче 1, можно доказать немало удивительных теорем. Например, нетрудно уста­новить, что все числа равны между собой или что у всех девушек глаза одинакового цвета. Последнее утверждение заслу­живает, нам кажется, того, чтобы остановиться на нем подробнее. Итак, соберем вместе совершенно произволь­ных n девушек, - тогда (сейчас мы это докажем) у них у всех глаза ока­жутся одинакового цвета. При n=1 это утверждение оче­видно (хотя и малосодержательно). Переход от n = k к n = k + 1 пояс­ним буквально «на пальцах».  Для этого возьмем k = 4, k + 1 = 5, по числу пальцев на руке. Согласно предположению индук­ции, у всяких четырех девушек глаза одинакового цвета. Соберем вместе 5 совершенно произволь­ных девушек (А, В, С, D и Е). По предположению индукции у любых четырех из них глаза одинакового цвета. В частности, у всех, кроме А, глаза такого же цвета, как у С,  и у всех, кроме Е, глаза тоже такого же цвета, как у С .Итак, у любых пяти де­вушек глаза одинакового цвета. При больших k доказательство проходит без всяких изменений (только, если вы захотите проводить его «на пальцах», вам, возможно, придется пригласить на помощь не­скольких приятелей).

 Найдите ошибку в рассуждении.

Задача 4. « О ленивых мудрецах »

                                                         Три дамы  А, В и  С сидят в купе

железнодорожного вагона с испачканными

                                                                 лицами и все три смеются. Внезапно

                                                                  А соображает: почему В не понимает,

                                                             что С смеется над ней? — О, боже!

                                         Они смеются надо мной.

Дж. Литлвуд. Математическая смесь.

Едут в вагоне поезда N мудрецов. За окнами прелестный пейзаж. Поезд то и дело ныряет в туннели. Дух захватывает. Собрались все мудрецы в коридоре вагона, в открытые окна глядят, не наглядятся.

Вдруг в одном туннеле грохот, дым, пыль. Проехали туннель — входит проводник. « Тут кое-кто испачкался, — говорит. — В поезде, к сожалению, воды нет. Но сейчас подряд большие остановки пойдут, так что можно будет выйти из поезда и помыться ».

Надобно вас теперь предупредить — мудрецы в вагоне собрались как на подбор: столь же умные, сколь ленивые. Никто, скажем, зря мыться не пойдет (если не знает наверняка, что испачкался). И у соседей не спросит, чистое у него лицо или грязное — зачем напрасно людей тревожить и самому беспокоиться? — проще сообразить.

Что же сделают мудрецы после объявления проводника?

Утверждается, что если у n из них испачканы лица, то ровно на n-й остановке все эти n мудрецов выйдут из поезда мыться.

Докажите сделанное утверждение по индукции.

М. Милг. Что сказал проводник? — http://kvant.mccme.ru

 

Ответы

”Расставим точки над і”

1.В задаче 3 переход от k=4 к  k+1=5 проделан без ошибок. Верно и то, что при больших k доказательство проходит без изменений. Нетрудно также перейти  от n=2 к n=3 и от n=3 к n=4. Не получится «только» переход от n=1 к n=2. Он не может получится потому, что при n=2 утверждение неверно: не у любых двух девушек глаза одинакового цвета.              

Если всё-таки попытаться провести доказательство «на пальцах» и в этом случае, то ничего не выйдет (в задаче 2 мы соединили А и Е «мостиком» С: и у А, и у Е глаза оказались какого же цвета, как у С; если пальцев всего два, то такого мостика нет). Двупалый ленивец из эпиграфа призван был привлечь внимание к указанному исключительному случаю.

2.В задаче 2(как и в задаче 1)  утверждение У верно, а все утверждения У, начиная со второго, неверны. Переход от n=k к n=k+1 обоснованы правильно для . Переход от n=1 к n=2 содержит ошибку: когда мы убираем карточку А , на столе остаётся одна карточка , на ней написано одна цифра , но вовсе не обязательно цифра X.  

3. Случай n = 1.При n = 1 утверждение выполняется. Мудрец М₁ с грязным лицом узнает из объявления, что в вагоне имеются  пассажиры с испачканными лицами. Оглядев соседей, он обнаружит, что у них лица чистые. Значит, грязное лицо — именно у него. Поэтому на 1-й остановке он идет мыться.

Переход от n = k  к  n = k+1. Покажем, что если утверждение справедливо при n = k, то оно верно и при n = k+1.

Пусть лица испачканы у мудрецов М₁,…, М_k+1.Тогда М_k+1 видит вокруг k грязных лиц (М₁,…,М_k) и рассуждает так:

Возможны два случая:

1.         у меня чистое  лицо;
2.         у меня грязное лицо.

В 1-м случае все k  мудрецов с грязными лицами, которых я вижу вокруг, выйдут умываться на k-й остановке (так как по предположению индукции при n=k утверждение справедливо).

Поскольку 1-й случай возможен, он не посчитает нужным выходить ни на k-й остановке, ни раньше.

Но возможен и 2-й случай: может быть, у меня тоже грязное лицо. Однако, каждый из перемазавшихся мудрецов М₁,…, М_k видит вокруг себя k испачканных лиц.В этой ситуации никто из них не пойдет умываться на k-й остановке.

Итак, если мудрецы  М₁,…, М_k не пойдут мыться  на k-й остановке, значит (k+1)-й грязный, и ему придется  идти умываться на (k+1)-й остановке.

Так рассуждают все мудрецы с грязными лицами. Следовательно, на (k+1)-й остановке все они пойдут умываться, что и требовалось доказать.

 Древнейшая прогрессия.

Древнейшая задача на прогрессии – не вопрос о вознаграждении изобретателя шахмат, насчитывающий за собой двухтысячелетнюю давность, а гораздо более старая задача о делении хлеба, которая была записана в знаменитом египетском папирусе Ринда. Папирус этот, разысканный Риндом в конце прошлого столетия, составлен около 2000 лет до нашей эры и является списком с другого, еще более древнего математического сочинения, относящегося, быть может, к третьему тысячелетию до нашей эры. В числе арифметических и геометрических задач этого документа имеется такая (приводим ее в вольной передаче):

 Задача 5.

 Сто мер хлеба разделить между пятью людьми так, чтобы второй получил на столько же больше первого, на сколько третий получил больше второго, четвертый больше третьего и пятый больше четвертого. Кроме того, двое первых должны получить в 7 раз меньше трех остальных. Сколько нужно дать каждому?

Решение

Очевидно, количества хлеба, полученные участниками раздела, составляют возрастающую арифметическую прогрессию. Пусть первый ее член , разность d. Тогда

доля первого …….

»   второго……….+ d

 »  третьего…….. ...+2 d

 »   четвертого…….+3 d

»   пятого …………+4d

 На основании условий задачи составляем следующие два уравнения:

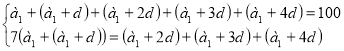
После упрощений первое уравнение получает вид , а второе . Решив эту систему, получаем: .

Значит, хлеб должен быть разделен на следующие части  .

Задача 6. «Алгебра на клетчатой бумаге»

Несмотря на пятидесятивековую древность этой задачи на прогрессии, в нашем школьном обиходе прогрессии появились сравнительно недавно. В учебнике Магницкого, изданном двести лет назад и служившем целых полвека основным руководством для школьного обучения, прогрессии хотя и имеются, но общих формул, связывающих входящие в них величины между собой, в нем не дано. Сам составитель учебника не без затруднений справлялся, поэтому с такими задачами. Между тем формулу суммы членов арифметической прогрессии легко вывести простым и наглядным приемом с помощью клетчатой бумаги. На такой бумаге любая арифметическая прогрессия изображается ступенчатой фигурой. Например, фигура ABDC на изображает прогрессию : 2;5;8;11;14.Чтобы  определить сумму ее членов, дополним чертеж до прямоугольника ABGE. Получим две равные фигуры ABDC и DGEC. Площадь каждой из них изображает сумму членов нашей прогрессии. Значит, двойная сумма прогрессии равна площади прямоугольника ABGE, т.е. .

 

 

 

 

 

 

 

 

 

 

 

 

Но AC+CE изображает сумму 1-го и 5-го членов прогрессии; AB – число членов прогрессии. Поэтому двойная сумма (число членов) или

Задача 7.«Поливка огорода»  

В огороде 30 грядок, каждая длиной 16 м и шириной 2,5 м. Поливая грядки, огородник приносит ведра с водой из колодца, расположенного в 14 м от края огорода (рис.2.2), и обходит грядки по меже, причем воды, приносимой за один раз, достаточно для поливки только одной грядки. Какой длины путь должен пройти огородник, поливая весь огород? Путь начинается и кончается у колодца.

Решение

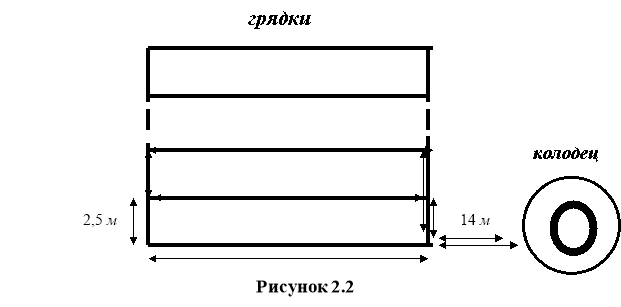Для поливки первой грядки он должен пройти путь 14+16+2,5+16+2,5++14=65 м.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тогда при поливке второй грядки он будет проходить 14+2,5+16+2,5+16+2,5+2,5+14=65+5=70 м.

Каждая следующая грядка требует пути на 5 метров длиннее предыдущей.

Имеем прогрессию: 65; 70; 75; 80;…; 65+5∙29.Сумма членов полученной прогрессии равна:

Огородник при поливке всего огорода проходит путь 4,125 километра.

Задача 8. «Яблоки»

Садовник продал первому покупателю половину всех своих яблок и еще пол-яблока, второму покупателю – половину оставшихся и еще пол-яблока; третьему – половину оставшихся и еще пол-яблока и т.д. Седьмому покупателю он продал половину оставшихся яблок и еще пол-яблока; после этого яблок у него не осталось. Сколько яблок было у садовника?

Решение

Если первоначальное число яблок х, то первый покупатель получил , второй , третий , … седьмой покупатель . Имеем уравнение или . Вычисляя стоящую в скобках сумму членов геометрической прогрессии, найдем: и . Всех яблок было 127.

Задача 9. «Покупка лошади »

В старинной арифметике Магницкого мы находим следующую забавную задачу, которую приводим, не сохраняя языка подлинника.

Некто продал лошадь за 156 руб. Но покупатель, приобретая лошадь, раздумал ее покупатель и возвратил продавцу, говоря:

-Нет мне расчета покупать за эту цену лошадь, которая таких денег не стоит.

Тогда продавец предложил другие условия:

-Если по-твоему цена лошади высока, то купи только ее подковные гвозди, лошадь же получишь тогда в придачу бесплатно. Гвоздей в каждой подкове 6. За первый гвоздь дай мне всего , за второй - , за третий - и т.д.

Покупатель, соблазненный низкой ценой и желая даром получить лошадь, принял условия продавца, рассчитывая, что за гвозди прийдется уплатить не более 10 рублей. На сколько покупатель проторговался?

Решение

За 24 подковных гвоздя пришлось уплатить копеек. Сумма эта равна 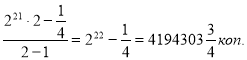, т.е. около 42 тысяч рублей. При таких условиях не обидно дать и лошадь в придачу.

Задача 10.«Вознаграждение воина »  

Служившему воину дано вознаграждение за первую рану 1 копейка, за другую – 2 копейки, за третью – 4 копейки и т.д. По исчислению нашлось, что воин получил всего вознаграждения 655 руб. 35 коп. Спрашивается число его ран.

Решение

Составляем уравнение или , откуда имеем: и - результат, который легко находим путем испытаний.

При столь великодушной системе вознаграждения воин должен получить 16 ран и остаться при этом в живых, чтобы удостоиться награды в 655 руб. 35 коп.

Задача 11.

Такое простое и даже очевидное утверждение: “Любое натуральное число можно разложить на простые множители” также требует доказательства.

Решение Воспользуемся математической индукцией. Пусть данная теорема верна, тогда если — простое, то оно само является своим разложением. Если же составное, то его можно представить в виде произведения хотя бы двух сомножителей: , где Но тогда . А по индуктивному предположению разлагаются на простые множители. Тогда же и тоже разлагается на простые множители. В данном примере применялось индуктивное рассуждение, которое осуществляет переход от всех чисел меньших , к .

Задача 12. На краю пустыни имеется большой запас бензина и машина, которая при полной заправке может проехать 50 километров. Имеются (в неограниченном количестве) канистры, в которые можно сливать бензин из бензобака машины и оставлять на хранение (в любой точке пустыне). Доказать, что машина может проехать любое расстояние. (Канистры с бензином возить не разрешается, пустые можно возить в любом количестве).

Решение. Попытаемся доказать индукцией по n, что машина может отъехать на n километров от края. При n ≤ 50 это известно. Осталось провести шаг  индукции и объяснить, как проехать n километров, если известно, что (n-1) километров, бензина может не хватить даже на обратную дорогу (не говоря уже охранении).

Будем доказывать, что мы не только можем проехать n километров, но и можем сделать сколь угодно большой запас бензина в точке на расстоянии n километров от края пустыни, оказавшись в этой точке после окончания перевозок.

Базис индукции (n = 1). Рейс на расстояние 1 обратно требует 2 единиц бензина (будем называть единицей количество бензина на километр пути), поэтому мы можем оставить 48 единиц бензина в хранилище (на расстоянии от края) и вернутся за новой порцией. (Осторожный человек оставлял бы чуть меньше — скажем, 47 единиц,  — чтобы не возвращаться с совсем уж пустым баком). Но так или иначе, за несколько рейсов в хранилище можно сделать запас произвольного размера, какого нам потребуется. (При этом коэффициент полезного действия составляет 48/50: чтобы создать 48 единиц запаса, мы расходуем 50 единиц.)

Шаг индукции. Мы должны научиться создавать хранилище на расстоянии n с любым заданным наперед запасом бензина (и оказаться у этого хранилища в конце перевозок). Как мы только что видели, это возможно, если  в точке n-1 имеется неограниченный запас бензина (базис индукции). Но по предположению индукции, мы можем запасти любое количество бензина (А единиц при сколь угодно большом А) на расстоянии n-1 от края!

Другими словами, если нам надо завезти заданное количество В бензина на расстоянии n от края, мы сначала представляем себе, что в n-1 бензина сколь угодно, и смотрим, какое количество (А) нам реально понадобится. Затем мы (пользуясь предположением индукции) завозим А единиц бензина в точку n-1.

Шень А. Математическая индукция. — М.: МЦНМО, 2004. — 36 с.

 

Упражнения

Аналогично рассмотренным примерам определить ошибку:

1. Вежливая очередь. Правило хорошего тона запрещает мужчине стоять в очереди сразу пред женщиной (он должен пропустить ее вперед).

  Поэтому, если первый человек в очереди — мужчина, то и все остальные — мужчины.

2. Резиновый автобус. Докажем, что в автобус помещается любое количество народу. В самом деле, один человек помещается без труда (базис индукции); с другой стороны, как бы ни был набит автобус, уж один-то человек в него всегда влезет (шаг индукции).

 

2.8.Парадокс изобретателя

В завершении приведем один очень интересный па­радокс, связанный с доказательством методом математиче­ской индукции.

Попробуем доказать 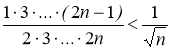. Базис индукции , после предположения об истинности при получим 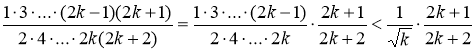остается доказать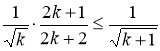, преобразуя это неравенство получаем , но это неверно, значит и все остальное неверно и исходное неравенство тоже.

Но это не так, попробуем теперь доказать 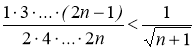данное неравенство сильнее исходного и доказать его казалось бы безнадежным делом, но все же попробуем это сделать.

Базис индукции 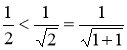, по предположению имеем

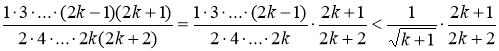
теперь надо доказать 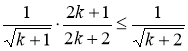преобразуя это неравенство получим , данное неравенство верно, значит верны и все предыдущие неравенства, и наше утверждение верно.

Как же это получилось? Дело в том, что хотя во втором случае нам и пришлось доказывать более сильное заключение, но мы могли пользоваться и более сильным предположением индукции. Подобная ситуация получила название парадокс изобретателя.

 

2.9.Контрольная работа по теме

“математическая индукция”

Контрольная работа

Вариант 1

1. Из-за своей слабости, даже против собственной воли, человек может поступить подло. Таким образом, слабость – подлость духа.

По глупости он может поступить подло, даже не помышляя о том. Таким образом, глупость – подлость ума.

В основе подлости лежат человеческая глупость и слабость.

Охарактеризовать данное умозаключение (вид, его справедливость). Привести свой пример умозаключения такого же вида.

2. Доказать, что для любого натурального n справедливо равенство: 1³+2³+3³+…+n³=n²(n+1)²/4.

3. Доказать, что при n>6 справедливо неравенство 3ⁿ>n2ⁿ⁺¹.

4. делится на .

5. Докажите,  что  n окружностей, расположенных на одной плоскости, делят  плоскость не более чем на n-n+2 частей.

Вариант 2

1. Иногда причиной подлости становится глупость, так как совершающий ее не осознает что, поступает подло.

Иногда слабость, так как, человек совершает ее под давлением обстоятельств, которым мог бы противостоять, будучи сильнее.

Глупость и слабость – вот причина подлости.

Охарактеризовать данное умозаключение (вид, его справедливость). Привести свой пример умозаключения такого же вида.

2.Доказать верность тождества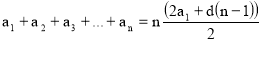 для любого натурального n.  (сумма арифметической прогрессии)

3. Доказать неравенство

4. Доказать, что при любом натуральном n число делится на 7.

5. Докажите, что существует многоугольник с любым числом сторон (начиная с четырех), имеющий ровно три острых угла.

Ответы и решения к контрольной работе

Вариант 1

1. Это есть индукция (научная).

2. Решение: 1) Пусть n=1. Тогда Х₁=1³=1²(1+1)²/4=1.

Мы видим, что при n=1 утверждение верно.  2) Предположим, что равенство верно при n=k

X_k=k²(k+1)²/4.  3) Докажем истинность этого утверждения для n=k+1, т.е. Х_k+1=(k+1)²(k+2)²/4.

X_k+1=1³+2³+…+k³+(k+1)³=k²(k+1)²/4+(k+1)³=(k²(k++1)²+4(k+1)³)/4=(k+1)²(k²+4k+4)/4=(k+1)²(k+2)²/4.

Из приведённого доказательства видно, что утверждение верно при n=k+1, следовательно, равенство верно при любом натуральном n.

3. Решение: Перепишем неравенство в виде (3/2)ⁿ>2n. При n=7 имеем 3⁷/2⁷=2187/128>14=27

неравенство верно. Предположим, что при n=k (3/2)^k>2k. 3) Докажем верность неравенства при n=k+1. 3^k+1/2^k+1=(3^k/2^k)(3/2)>2k(3/2)=3k>2(k+1).

Так как k>7, последнее неравенство очевидно. В силу метода математической индукции неравенство справедливо для любого натурального n.

4. Решение: При n=1 утверждение верно:

Предположим, что оно верно для n=k

Докажем его справедливость для n=k+1

где — некоторое натуральное число. Раскрывая скобки, получим :

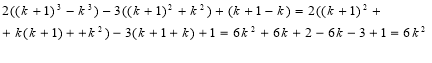Из приведённого доказательства видно, что утверждение верно при n=k+1, следовательно, равенство верно при любом натуральном n.

 5. Решение.

Для n=1 утверждение справедливо, т.к.одна окружность делит плоскость на

(-1+2)=2 части; пусть утверждение справедливо для n=k, докажем его справедливость для n=k+1. Выберем одну из окружностей, тогда, во-первых, она пересечётся c каждой из остальных k окружностей не более в двух точках, во-вторых, оставшиеся k окружностей делят плоскость не более чем на(k-k+2) частей (в силу принципа индукции). Полученные (не более чем 2k) точки пересечения выбранной окружности с остальными разделят её не более чем на 2k частей, каждая из этих дуг разделит одну из имевшихся частей плоскости на две. Итак, к имевшимся не более чем  (k-k+2) частям добавиться не более чем  2k частей. Всего получим не более чем

(частей).

Вариант 2

1. Это есть индукция (научная).

2. Решение: 1) При n=1 тождество верно

2) Предположим, что при n=k   3) Докажем, что тождество верно при n=k+1.

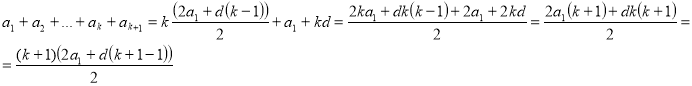Из приведённого доказательства видно, что утверждение верно при любом натуральном n.

3. Решение:  При n=1 неравенство верно . Предположим, что при n=k . Докажем справедливость неравенства при n=k+1

Последнее очевидно, а поэтому в силу метода математической индукции неравенство доказано.       

4. Решение: При n=1 утверждение верно, 35 делится на 7. Предположим, что утверждение верно и при n=k и докажем справедливость утверждения при n=k+1 Имеем:

Полученное число делится на 7, т.к. представляет собой разность двух чисел, кратных семи.

5.Решение: Докажем индукцией по числу сторон многоугольника.

База: n=4. Построить четырехугольник с тремя острыми углами нетрудно. Например, пристроив к основанию равнобедренного треугольника с углами 20, 20, 140, равносторонний треугольник с такой же стороной, получаем четырехугольник с углами 60, 80, 80, 140.

Переход: (от n сторон к n+1 стороне). Возьмем какой-нибудь тупой угол нашего n-угольника (их у нас n-3) и “отпилим” (см. рис.). Появятся два новых тупых угла (тупые, так как смежные с ними острые — они лежат в одном треугольнике с исходным тупым углом), т.е. получим n+1 угольник. А три острые угла в нем останутся, и т. д.

 

 

Заключение

Метод математической индукции является одним из высокоэффективных методов поиска новых результатов и доказательства истинности выдвинутых предположений.

Хотя этот метод в математике и не нов, но не будет преувеличением сказать, что интерес исследователей к нему возрастает в связи с развитием так называемой дискретной математики.

Надо учить учащихся умело использовать этот метод, рассредоточив его применение по всему курсу математики. Тем самым упрощаются доказательства многих рассуждений или появляется возможность посмотреть на одни и те же факты и явления с разных сторон. Поэтому владение этим методом рассуждения значительно расширяет возможности учащихся.

Данная работа может быть полезна для подготовки к занятиям школы юных математиков при Донецком национальном университете по теме «Метод математической индукции», как дидактический материал для учащихся 9 классов, серьезно увлекающихся математикой или может быть использована учащимися как методическое пособие для самостоятельного овладения методом математической индукции.

Известный математик А.Н. Колмогоров считал: «Понимание и умение применять метод математической индукции является хорошим критерием логической зрелости, которая совершенно необходима математику.» [Колмогоров А.Н. «О профессии математика» Изд-во МГУ 1960г.]

 

Приложение

(А) Ответы к задачам на самостоятельное решение (стр.2.2)

Решение1.

Проверим справедливость для n=1.S(1)=1 S(1)= ===1.

Для n=1 формула верна. Предположим, что она верна для какого-либо натурального n=k,т.е.

S(k)=.

Докажем, что она будет верна и для n=k+1 т.е.

S(k+1)=1³+2³+3³+…+k³+(k+1)³=.

S(k+1)=S(k)+(k+1)³=+(k+1)³===               =.

Мы получили ту же формулу, т.е. мы доказали, что формула верна и для n=k+1.Следовательно, в силу принципа математической индукции данная формула верна для любого  натурального n.

Решение 2.

Проверим справедливость для n=2

S(2)= ;  S(2)==;

Для n=2 формула верна. Предположим, что она верна для какого-либо натурального n=k, т.е.

**…=,

Докажем, что она будет верна и для n=k+1 т.е.

**…*=;

*====;

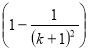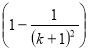Мы получили ту же формулу, т.е. мы доказали, что формула верна и для n=k+1.Следовательно, в силу принципа математической индукции данная формула верна для любого  натурального n.

Решение 3.

Проверим справедливость для n=1

S(1)=, S(1)= )===.

Для n=1 формула верна. Предположим, что она верна для какого-либо натурального n=k, т.е

S(k)= )

Докажем, что она будет верна и для n=k+1 т.е.

S(k+1)= +-+…+(-1)+(-1)= ).       S(k+1)=S(k)+(1)=)+(1)=   +(-1)*= ====

==

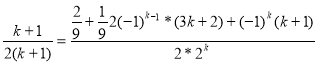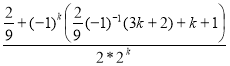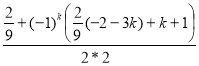Мы получили ту же формулу, т.е. мы доказали, что формула верна и для n=k+1.Следовательно, в силу принципа математической индукции данная формула верна для любого  натурального n.

Решение 4.

Проверим справедливость для n=1

S(1)= S(1)=

Для n=1 формула верна. Предположим, что она верна для какого-либо натурального n=k, т.е

S(k)=

Докажем, что она будет верна и для n=k+1 т.е.

 

S(k+1)= .

S(k+1)= =

==  =.

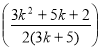Мы получили ту же формулу, т.е. мы доказали, что формула верна и для n=k+1.Следовательно, в силу принципа математической индукции данная формула верна для любого  натурального n.

(В) Доказательство к задаче на самостоятельное решение (стр.2.3)

Запишем n-ю строку таблицы n,(n+1)…...(2n-1)…Исходя из условия таблицы, видим, что в каждой строке, чтобы получить следующее нечётное число, порядковый номер которого равен номеру строки, то нужно к предыдущему номеру строки прибавить 2 т.е.  (2n-1)+2

Проверим справедливость для n=1

S(1)=1   S(1)=(2*1-1)=1-верно.

Предположим, что это верно для n слагаемых

S(n)=(2n-1)

Докажем, что это будет верно и для n=n+1 слагаемых и запишем строку для n+1 слагаемых.

(n+1)……(2(n+1)-1),т.е. (n+1)слагаемых равно(2n+1).

Отсюда S(n+1)=(2n+1)

Докажем это

S(n+1)=((2n-1)+2)=(2n-1+2)=(2n+1)-это и есть (n+1)  слагаемых , что и требовалось доказать.

Видно также, что сумма чисел в строке равно произведению данного нечетного числа на число чисел в строке, а число чисел в строке равно числу, порядковый номер которого равен номеру строки от начала таблицы.

(С) Доказательства к задачам на самостоятельное решение(стр.2.4)

Доказательство 1.

При n=4 имеем  , т.е. для n=4 неравенство справедливо.

Предположим, что оно верно для некоторого натурального n=k, т.е.

+…+

Докажем, что оно будет верна и для n=k+1т.е. +…++

= т.к.

Неравенство доказано.

Доказательство 2.

При n=3 имеем 16>16-3 – неравенство верно.

Предположим, что оно верно для некоторого натурального n=k, т.е.

2 где k ≥ 3. Докажем, что тогда оно верно и для  n=k+1,т.е.

2 Преобразуем стороны уравнения.

=+>т.к. >0 при k≥3    Неравенство доказано

Доказательство3. При n=2 получим

Неравенство верно. Предположим , что оно верно при некотором натуральном n=k.

Докажем, что оно будет верно и для n=k+1 т.е.

Преобразует левую часть неравенства

+

+ т.к. >0.

Неравенство доказано.

(D) Доказательства к задачам на самостоятельное решение (стр.2.5)

Доказательство 1.

S(n)= ().

База индукции выполняется, потому что F=9-8-9=64 и F.

Пусть предположение индукции верно, то есть F. Тогда имеем : 9-8(k+1)-9

= 9*9-8k-8-9=(9-8k-9)+(8*9-8)=F+8(9-1). Выражение 8(9-1) делится на 16, потому что 9-1- парный член при любом k. Потому что F из предположения, то 9-8(k+1)-9 (то есть F) делится на 16. Значит, Утверждение S(k) S(k+1) тоже верно. И утверждение задачи доказано, то есть для любого n S(n) верно.

Доказательство 2.

В данном случае можно использовать утверждение: Если число a делится на каждое из чисел b,c , которые попарно взаимно-простые, то a делится на их произведение bc (утверждение справедливо для любой конечной последовательности попарно взаимно-простых делителей).

В нашем случае нужно доказать, что k- k делится на 2,3и 5. Для этого разложим k- k  на множители: k- k=(k-1)k(k+1) (k+1). Произведение(k+1)k делится на 2, потому, что одно из чисел k+1,k- парное. Произведение (k-1)k(k+1) делится на три. Действительно, относительно деления на3 для k возможны случаи : k=3m, k=3m +1,k=3m+2.

легко убедится, что для каждого из этих случаев число (k-1)k(k+1),а значит, и число k- k делится на 3. Чтобы убедится, что k- k делится на 5, рассмотрим возможности подачи числа k относительно деления на 5: k=5m, k=5m+1, k=5m+2,k=5m+3, k=5m+4 и, пользуясь разложением k- k=(k-1)k(k+1) (k+1), получим, что в каждом из этих случаев k- k делится на 5. Например, если k=5m+2, то множитель k+1 делится на 5.

Действительно, k+1=(5m+2) +1=25 m+20 m+4+1=5(m+4 m+1).

Значит, k- k делится на 2,3и 5, а значит, делится и на их произведение 30.

(I) Решение к задачам на самостоятельное решение (стр.2.6)

Решение 1.

Предварительно докажем , что n точек, расположенных на прямой, делят её на n+1 частей.

Проверим справедливость для n=1 , утверждение верно т. к. , а одна прямая делит плоскость на две части. Предположим, что утверждение верно для какого-либо натурального n=k,т.е.   k прямых делит плоскость на частей. Докажем, что утверждение верно для n=. Выберем одну из k+1 прямых и будем называть (k+1)-й. В силу предположения индукции оставшиеся k прямых разделят плоскость на частей;(k+1)-я прямая пересечёт k первых в k точках и потому разделится этими точками на k+1 частей . Так как полученные k точек отличны от точек пересечения k первых прямых между, то каждая из этих частей разбивает одну из имевшихся частей плоскости на две части, т.е. к имевшимся частям добавится ещё k+1 .

Всего получим

+ (k+1)=(частей).

Мы получили ту же формулу, т.е. мы доказали, что утверждение верно и для n=k+1.Следовательно, в силу принципа математической индукции данное утверждение верно для любого  натурального n.

Решение 2.

При n =1 утверждение справедливо, так как одна плоскость делит пространство на две части и

=, предположим, что утверждение верно для n=k, и докажем его справедливость для n=k+1. Выберем одну из плоскостей, тогда, во-первых для прямых её пересечения с остальными k плоскостями будут выполнены условия предыдущей задачи, поэтому выбранная плоскость разделится этими прямыми на

   частей; во-вторых, силу предположения индукции оставшиеся k плоскостей разделят пространство на частей.

Каждая часть выбранной плоскости разделит одну из имевшихся частей на две (это обеспечивается условием задачи). Всего получим

(частей).

Решение 3.

Для n=1 утверждение справедливо, т.к.одна окружность делит плоскость на (-1+2)=2 части; пусть утверждение справедливо для n=k, докажем его справедливость для n=k+1. Выберем одну из окружностей, тогда, во-первых, она пересечётся c каждой из остальных k окружностей не более в двух точках, во-вторых, оставшиеся k окружностей делят плоскость не более чем на(k-k+2) частей (в силу принципа индукции). Полученные (не более чем 2k) точки пересечения выбранной окружности с остальными разделят её не более чем на 2k частей, каждая из этих дуг разделит одну из имевшихся частей плоскости на две. Итак, к имевшимся не более чем (k-k+2) частям добавиться не более чем  2k частей. Всего получим не более чем

(частей).

 

 

Использованная литература

Книга одного автора

1.           Алексюк А.М. Общие методы обучения в школе.- Киев: Радянська школа, 1981.
2.           Бабинская И.Л. Задачи математических олимпиад. – М.: Наука, 1975.
3.           Бевз Г.П. Алгебра: Учебник для 7-9 классов. - Киев: Вежа, 2001.
4.           Виленкин Н. Я. Индукция. Комбинаторика. – М., 1976.
5.           Демпан И.Я. История арифметики. – М., 1965.
6.           Каганов Э.Д. 400 самых интересных задач с решениями по школьному курсу математике для 6-11 классов. - М. - ЮНВЕС. - 1997. - 288 с. ISBN 5-88682-029-9.
7.           Кра­мор В.С.  Алгебра и начала анализа (система проведения занятий на подготовительных отделениях вузов): Учеб. пособие для подготовительных отделений вузов - М.: Высш. школа, 1981. - 336 с., ил.
8.           Пойа Дж. Как решать задачу. – М.: Учпедгиз, 1961.
9.           Родосский К.А. Обобщённая форма полной математической индукции // Ма­тематика в школе - 1975. - № 1 - c. 8.
10.      Слепкань З.И. Формирование творческой личности ученика в процессе обучения математики, Математическая школа. – 2003. – №3.
11.      Соминский И.С. Метод математической индукции-М.-1974.
12.      Стройк Д.Я. Краткий очерк истории математики. – М.: Наука, 1984.
13.      Фихтенгольц Г.М. Основы математического анализа 2001г
14.      Шарыгин И.Ф. Факультативный курс по математике: Решение задач. Учебное пособие для 10кл. средней школы. – М.: Просвещение, 1989

Книга двух авторов

 

1.           Головина Л.И., Яглом И.М. Индукция в геометрии. Популярные лекции по математике, вып. 21. - М.: Физматгиз, 1961. - 100 с.: ил.
2.           Головина Л.И., Яглом И.М. Индукция в геометрии. – М., 1970.дакция физико-математической литературы, 1983. - 384 с.
3.           Колмогоров А.Н., Шварцбурд С.И. Алгебра и начала анализа. Метод мате­матической индукции // Математика в школе - 1975. - № 1 - с. 8 -14.

Книга четырех авторов

1.      Абрамов А.М, Ивлев Б.М., Дудницын Ю.П., Шварц­бурд С.И.. Задачи повышенной трудности  по алгебре и началам анализа: Учеб. пособие для 10-11 кл. сред. шк.. - М.: Просвещение, 1990. - 48 с.: ил. : ISBN 5-09-003597-0.
2.      Александров Б.И., Максимов В.М., Лурье М.В., Колесниченко А.В. Пособие по математике для поступающих в вузы. Изд-во МГУ, 1972.
3.      ДемидовИ.Т,КолмогоровА.Н.,ШварцбургС.И., Ивашев-Мусатов О.С.Алгебра и начало анализа. Учебное пособие «Просвещение» 1975.

 

 

Сайты

1.http://pedagogika.by.ru/

2.http://works.fio.ru/rsk/r3/4410.htm