Творчо-пошукова робота "Цікаві дроби"
КРИВОРІЗЬКА ГІМНАЗІЯ №109 “ТЕМП”
КРИВОРІЗЬКОЇ МІСЬКОЇ РАДИ
Цікаві дроби
Творчо-пошукова робота учениці 6 класу
Криворізької гімназії №109 “Темп” Мерешко Олександри Вікторівни
Науковий керівник
Маренич Катерина Василівна
м. Кривий Ріг
2023
Цікаві дроби
Вступ
Розділ І. Історія виникнення звичайних дробів
1.1 Поява звичайних дробів
1.2 Дроби в стародавньому Єгипті
1.3 Дроби у стародавньому Вавилоні
1.4 Дроби в стародавній Греції
1.5 Дроби в давньому Римі
1.6 Дроби в інших державах давнини
Розділ ІІ. Дроби в мистецтві
2.1. Дроби і музика
2.2 Дроби та хореографія
2.3 Дроби в мистецтві живопису та фотомистецтві
2.4 Дроби в архітектурі та скульптурі
2.5 Дроби і література
Висновки
Використані джерела
Додатки
Вступ
Світ захоплень сучасної дитини різноманітний. Дітям подобається співати, малювати, танцювати, знімати власні відеоролики, тощо. Їх приваблює все красиве та чарівне. Але дуже мало хто бачить красу та чарівність в математиці. Так вже склалося, що більшість людей називають математику сухою та не цікавою наукою. Вважають, що математика займається виключно числами, нудними розрахунками та вимірюваннями. А ще найбільші складнощі виникають у людей при використанні дробів. Навіть існує німецька приказка "попасти в дроби", що означає опинитися в скрутному становищі. Але математика - це дещо більше, ніж розрахунки, а дроби навіть дуже цікаві. Без дробів життя було б нецікавим. Дроби дають емоції, забарвлюють та урізноманітнюють світ. І так ще в давнину вважали дуже шановані люди. Історія дробів налічує не одне тисячоліття. Зазирнемо в її глибини.
Вивчаючи історію музики, я дізналась про те, що саме завдяки музиці з'явилися дроби в грецьких науках. Вивчаючи закони музики, я побачила наскільки важливим є використання дробів. Мене зацікавило питання використання дробів в інших сферах мистецтва та історія виникнення дробів.
Актуальність і доцільність роботи полягає систематизації та узагальненні матеріалів з різних джерел щодо історії виникнення та розвитку уявлення про дроби та значущість використання дробів у повсякденному житті.
Мета дослідження: сформувати уявлення про виникнення і розвиток звичайних дробів, дослідити використання дробів в мистецтві, стимулювати цікавість до математики.
Зміст поставлених завдань: розвивати вміння здійснювати пошук інформації; розвивати вміння працювати з додатковою літературою; збагатити світогляд; розвивати вміння структурувати та узагальнювати отриману інформацію.
Об'єкт дослідження: звичайні дроби.
Предмет дослідження: виникнення звичайних дробів та розвиток уявлення про звичайні дроби та галузі їх застосування.
Методи дослідження: збір та аналіз літератури з теми, порівняння та узагальнення матеріалу.
Проект має теоретичний характер.
Практичне значення дослідження: можливість застосування результатів для популяризації математичних знань, міжпредметних зв'язків.
Особистий внесок полягає у особливості систематизації та викладення матеріалів дослідження.
Розділ І. Історія виникнення звичайних дробів
1.1 Поява звичайних дробів
Математика має довгу цікаву історію, що сягає глибині віків. Дробові числа виникли не відразу. Але історія дробів налічує не одне тисячоліття. Розділ “Дроби і дії з дробами” і зараз вважається одним із найскладніших розділів математики. Не всі люди мають достатнє уявлення про дроби та не розуміють дроби. Іноді це призводить до казусів. Відомо, що на початку 1980-х років мережа ресторанів швидкого харчування A&W запустила рекламну кампанію власного гамбургера. Кампанія акцентувала увагу на тому, що, на відміну від бургера в 1/4 фунта з McDonald’s, гамбургер A&W важив 1/3 фунта і коштував дешевше. Він подобався користувачам. Незважаючи на це, кампанія провалилася. Пізніше A&W провела дослідження й виявила причину: багато клієнтів просто не розуміли значення дробових чисел. Пропозиція здавалася їм невигідною, тому що 3 менше за 4. Так нерозуміння дробів призвело до фіаско.
Яку ж історію мають дроби? Який початок мають? Дроби з'явилися тоді, коли виникла необхідність ділити ціле на частини. Уміння ділити ціле на частини виникло на території стародавнього Єгипту та Вавилону. Поява дробів пов'язана з вирішенням господарських потреб: поділити здобич порівну, виміряти земельну ділянку, якщо її довжина і ширина не вкладається в ціле число кроків, тощо.
Сам термін «дріб» має арабське коріння і походить від слова, що позначає «ламати, розділяти». Сучасне визначення звучить так: дріб — це частина або сума частин одиниці. Дії з дробами являють собою послідовне виконання математичних операцій з частками чисел.
У кожної держави стародавнього світу були свої особливості у «взаєминах» з цим розділом математики. Як вже зазначали, вперше оперувати дробами почали на території Єгипту і Вавилона. Підхід математиків цих двох держав мав значні відмінності. Однак початок і там і там було покладено однаково. Першим дробом стала половина або 1/2. Далі виникла чверть, третина і так далі. Згідно з даними археологічних розкопок, історія виникнення дробів налічує близько 5 тисяч років. Вперше частки числа зустрічаються в єгипетських папірусах, і на вавилонських глиняних табличках.
1.2 Дроби в стародавньому Єгипті
Єгипетські дроби являють собою суму кількох доданків виду 1/n. Чисельник
— завжди одиниця, а знаменник — натуральне число. Дроби записувалися за допомогою ієрогліфів. Сам дріб записували так: ціле число з овалом над ним. Тобто зображення 3 і овал над ним означало 1/3 (див. додаток 1).
Отже у єгиптян не було дробів з чисельником, відмінним від 1, тобто дробів виду 2/3 або 5/6. Оперували вони також лише дробами з чисельником 1. А як же тоді написати дріб 5/6? Єгипетські математики розкладали такі дроби на дроби з чисельником 1. Отже 5/6 – це 1/2 + 1/3 (тобто 2 і 3 з овалом вгорі) (додаток 1). При розрахунках усі частки намагалися записувати у вигляді таких сум. Наприклад, 5/24 = 1/8 +1/12 . Окремі позначення мали тільки дроби 2/3 та 3/4, а інші розбивалися на складові. Існували спеціальні таблиці, в яких частки числа представлялися у вигляді суми. Найдавніша з відомих згадок такої системи зустрічається у Математичному папірусі Рінда, датованому початком другого тисячоліття до нашої ери (додаток 2). Він включає таблицю дробів і математичні задачі з рішеннями і відповідями, поданими у вигляді сум дробів. Єгиптяни вміли складати, ділити і множити частки числа. Подання частки числа у вигляді суми доданків виду 1/n, характерну для стародавнього Єгипту, використовувалося математиками не тільки цієї країни. Аж до Середніх століть єгипетські дроби застосовувалися на території Греції та інших держав.
1.3 Дроби у стародавньому Вавилоні
Розрахункова техніка у Вавилоні було зручніше і досконаліше, ніж у Єгипті. Математика в цій країні вирішувала набагато більше коло завдань. Про це свідчать записи на збережених глиняних табличках, що заповнені клинописом. Завдяки особливостям матеріалу вони дійшли до нас у великій кількості ( додаток 3).
Історія виникнення дробів у Вавилоні безпосередньо пов'язана з особливостями системи числення, що дісталася древній державі у спадок від шумеро-аккадської цивілізації. Колись два кочових населення: сумерійці і акадяни злилися в потужну державу – Вавилон. На час злиття кожен з цих народів мав свої вагові та грошові одиниці. Основною одиницею у сумерійців була «міна», а у акадян - «шекель». «Шекель» була приблизно в 60 разів менше «міни». Ваговою одиницею встановили «талант», вона була в 60 разів більше «міни». Вчені вважають, що походження шістдесяткової системи числення у вавилонян пов'язано з тим, що вавилонська грошова і вагова одиниця виміру поділялися в силу історичних умов на 60 рівних частин: 1 талант = 60 мін; 1 міна = 60 шекель.
Отже, система числення у Вавилоні була шістдесяткова. Кожен новий розряд відрізнявся від попереднього на 60. Така система збереглася в сучасному світі для позначення часу і величин кутів. Дроби також були шестидесятеричными. Для запису використовували спеціальні значки. Письмова шістдесяткова нумерація вавилонян комбінувалася їх двох значків: вертикального клина ▼, так позначали одиницю, і кутового знака ◄, так позначали десять. У вавилонських клинописних текстах вперше зустрічається позиційна система числення. Вертикальний клин позначав не тільки 1, але і 60, 602, 603 і т.д. Знака для нуля в позиційній шістдесятковій системі у вавилонян спочатку не було. Пізніше був введений знак, який замінює сучасний нуль, для відділення розрядів між собою. Шістдесяті частки були звичні в житті вавилонян, вони записували всі дроби зі знаменником 60 або його степеня. Наприклад, запис у вавилонян 4; 52; 03 означає 4 + 52/60 + 3/(602).
Як і в Єгипті, приклади з дробами містили окремі символи для позначення 1/2,
1/3 і 2/3. Вавилонська система не зникла разом з державою. Дробами, написаними в 60-тирічной системі, користувались античні і арабські астрономи і математики.
1.4 Дроби в стародавній Греції
Історія звичайних дробів мало чим збагатилася в стародавній Греції. Жителі Еллади вважали, що математика повинна оперувати лише цілими числами. Тому вирази з дробами на сторінках давньогрецьких трактатів практично не зустрічалися. Проте певний внесок у цей розділ математики внесли піфагорійці. Вони розуміли дроби як відношення або пропорції, а одиницю вважали неподільною. Піфагор з учнями побудував загальну теорію дробів, навчився проводити всі чотири арифметичні операції, а також порівняння дробів шляхом приведення їх до спільного знаменника. Греки вільно оперували всіма арифметичними діями з дробами, але числами їх не визнавали. Наряду з одиничними, «єгипетськими» дробами греки вживали і загальні звичайні дроби. Серед різних записів вживалася і така: зверху знаменник, під ним – чисельник дробу. Наприклад, 5/3 означало три п'ятих і т.д
1.5 Дроби в давньому Римі
Римська система дробів була пов'язана з мірою ваги, званої «асс». Вона ділилася на 12 часток. 1/12 асса називалася унцією. Для дробів, знаменник яких отримували шляхом ділення частки на більш дрібні, були особливі назви. Для позначення дробів існувало 18 назв. Коли ми чуємо фразу: «Він скрупульозно вивчив це питання», то розуміємо, що питання вивчене до кінця, що жодної найменшої неясності не залишилося. А слово «скрупульозно» від римської назви аса - «скрупулус». Користувались і такими назвами: «семіс» - половина аса, «секстане» - шоста частка аса, «семіунція» – півунція, або 1/24 аса, тощо. Щоб працювати з дробом, треба було пам'ятати для цих дробів і таблицю додавання, і таблицю множення. Для полегшення роботи складалися спеціальні таблиці, деякі з них дійшли до нас. Незручність такої системи полягала в неможливості подати число у вигляді дробу зі знаменником 10 або 100. Римські математики подолали труднощі з допомогою використання відсотків.
1.6 Дроби в інших державах давнини
Приблизно у II ст.н.е. в китайському трактаті «Математика в дев'яти книгах» вже викладені прийоми скорочення дробів та всі дії з дробами. Книга була призначена для землемірів, техніків і рахункових працівників. Якщо історія виникнення звичайних дробів почалася в Єгипті та Вавилоні, то десяткові вперше з'явилися в Китаї. У Піднебесній імперії їх стали використовувати приблизно з III століття до нашої ери. Історія десяткових дробів почалася з китайського математика Лю Хуэя, який запропонував використовувати їх при витяганні квадратних коренів. У III столітті нашої ери десяткові дроби в Китаї стали застосовуватися при розрахунку ваги та об'єму. Поступово вони все глибше почали проникати в математику. У Європі, однак, десяткові дроби стали застосовуватися набагато пізніше.
Індія, одна з найдавніших і величних країн світу, є батьківщиною позиційної десяткової нумерації (V-VII ст.н.е.). Індійці широко вживали «звичайні» дроби. Позначення звичайних дробів за допомогою чисельника і знаменника було прийнято в Індії ще в VIII ст.н.е., але запис був без риски дробу. Чисельник і знаменник записуються так само, як і у нас зараз, але без горизонтальної риски, а просто розміщуються один над іншим. Дробову риску стали застосовувати лише в XIII столітті. Близько 1500 років тому індуси першими почали відокремлювати рискою чисельник від знаменника.
У VII ст.н.е. відомий вірменський вчений Ананій Ширакаці писав книги з математики, географії та астрономії. Він склав величезні таблиці додавання, віднімання і множення чисел. Серед книг Ананія є також арифметика і збірник задач, названий «Питання і відповіді». 1300 років тому Ананій розв’язував завдання з дробами, які навіть для багатьох вчених з Європи на той час здавалися важкими.
Сьогодні, як і раніше, в числі найскладніших розділів математики називаються дроби. Історія дробів не була простою. Різні народи іноді незалежно один від одного, а іноді запозичуючи досвід попередників, прийшли до необхідності впровадження, освоєння і застосування частки числа. Вчення про дроби виникало з практичних спостережень і завдяки нагальним проблемам. Необхідно було ділити хліб, розмічати рівні ділянки землі, вираховувати податки, вимірювати час, тощо. Особливості застосування дробів і математичних операцій з ними залежали від системи числення в державі і від загального рівня розвитку математики. Так чи інакше, подолавши не одну тисячу років, розділ математики, присвячений часткам чисел, сформувався, розвинувся і з успіхом використовується сьогодні для самих різних потреб як практичного характеру, так і теоретичного. Кожна дитина, що навчається в школі, вже вивчає і буде вивчати далі дроби і дії з дробами. Тобто робить те, що робили обрані люди ще до нашої ери. Те, що вміння обчислювати і вміння працювати з дробами необхідно людям технічних професій, не викликає сумнівів. Але чи потрібно все це людям мистецтва? Далі розглянемо наскільки важливими є дроби, розуміння дробів (навіть підсвідоме) в мистецтві.
Розділ ІІ. Дроби в мистецтві
У кожного з нас є свій дарунок від природи. Хтось складає вірші, хтось співає, хтось малює, хтось вміє робити все це відразу. Чи допомагає нам у цьому математика?
Математика та мистецтво тісно пов'язані. Математику описували як мистецтво, мотивоване красою. Математика існує в таких мистецтвах як музика, танець, малярство, архітектура, скульптура та текстиль.
2.1. Дроби і музика
«Музика є прихoвана арифметична вправа душi, щo не вмiє рахувати" (Лейбніц). "Музика - це прoяв прихoванoї математики" (Гольдбах). Альберт Ейнштейн вважав, що і справжня наука і справжня музика потребують однорідного розумового процесу.
Одним з перших, хто спробував висловити красу музики за допомогою чисел був Піфагор. Він створив власну школу мудрості, поклавши в її основу два мистецтва: математику та музику. Піфагор вважав, що гармонія чисел схожа на гармонію звуків. І музику треба сприймати не як ремесло, а як наукову дисципліну.
І мова математики, і мова музики – інтернаціональні! Для них не існує кордонів і не потрібні словники. Математика і музика стоять в одному ряду як найвищі надбання людського генію.
Музика не може обійтися без нот. Кожна нота має певну тривалість. Дроби увійшли у математику давніх греків саме завдяки музиці. Згадайте: греки оперували дробами, але не вважали їх числами. У назвах тривалості нот застосовуються дроби. Тривалості нот бувають цілими, половинними, четвертними, восьмими, тощо.
Міркування Піфагора були такі: ціла струна звучить як - "до", половина - "ре", четвертина - "мі", восьма - "фа". Для вивчення коливань струни використовували прилад під назвою монохорд, що являє собою єдину струну, закріплену у двох точках над резонатором. Піфагор довів, що довжина струн, які при однаковому натягуванні дають ноти до, мі, соль, пропорційні числам 1, 4/5, 2/3. А число 4/5 є середнім гармонійним 1 і 2/3. Звідси і прийшло до математики поняття гармонії.
Піфагор дослідним шляхом встановив, що 2/3 натягнутої на монохорді струни, що приведена у коливання, дають звук точно на чисту квінту вище основного тону, 3/4 струни дають кварту, а половина струни – октаву. Музика, як і математика, прагне гармонії.
Знаннями про дроби користувалися майстри, які виготовляли музичні інструменти. Наприклад, сопілки: на половині довжини свердлять дірочку - це "до", на третині - "ре", на четвертині - "мі". Дроби використовують при розрахунках для виготовлення дзвонів. Наприклад, церковний дзвін для красивого звучання повинні мати 81,94 % - міді, 17,21 % - олова, 0,035 % - сірки.
2.2 Дроби та хореографія
У хореографії і танцях використовують поняття такту. Такт - це метрична одиниця, базова міра тривалості музики і танцю. Головна характеристика такту музичний розмір, який надається у вигляді дробів. Наприклад, 2/4,3/4, 6/8. В чисельнику записують кількість долей в такті, а в знаменнику вказують їх тривалість в нотних одиницях. Такт завжди починається з сильної долі та містить хоча б одну слабку долю. Як правило, з існуючих тактів для танцю найчастіше використовують 2/4, 3/4 , або 4/4, 3/8, 6/8. Вальс має розмір 3/4, марш 2/4 або 4/4.
2.3 Дроби в мистецтві живопису та фотомистецтві
В епоху відродження художники відкрили, що будь-яка картина має певні точки, що приковують погляд, так звані зорові центри. При цьому не має значення який формат має картина – горизонтальний або вертикальний. Таких точок всього чотири, вони розташовані на відстані 3/8 і 5/8 від відповідних країв площини. Це відкриття отримало назву «золотий поділ» картини. Тому, для того, щоб привернути увагу до головного елементу фотографії , необхідно сполучити цей елемент з одним із зорових центрів.
Портрет Мони Лізи (Джоконди) довгий час привертав увагу досліджувальників, які зрозуміли, що композиція малюнку основана на золотих трикутниках (додаток 4).
«Золотим поділом” або “божественною пропорцією” називали математики середньовіччя поділ відрізки, при якому довжина всього відрізку відноситься до довжини його більшої частини, як довжина більшої частини до меншої. Це відношення дорівнює 5/8, або, приблизно = 0,618. (додаток 5)
У фотомистецтві використовують також правило діагонального золотого перерізу. Це ще одне правило застосування «золотого перерізу». Накладаємо діагональну сітку на зображення таким чином, як показано на фото. Головні об'єкти зображення мають бути розташовані в отриманих секціях (додаток 6).
Також у фотомистецтві використовують правило третин. Кадр поділяють на три рівні частини і по горизонталі і по вертикалі. Отримуємо сітку, яку бачимо на зображені. Об'єкти, що розташовані в точках перетину ліній відповідають найкращому зоровому сприйняттю. Отже важливий об'єкт зйомки треба розташовувати або вздовж ліній, або в точках перетину ліній сітки (додаток 7).
2.4 Дроби в архітектурі та скульптурі
З усіх видів мистецтва архітектура, мабуть, ближче з усіх до математики: тому що за основу конструкцій покладені найточніші розрахунки. У давнину, окрім відомих нині дев'яти муз, існувала і муза математики, тобто математика вважалася мистецтвом рівним астрономії, муза якої входить в склад свити Аполлона – ватажка усіх муз. Так і уявляєш собі, що по один бік Математики стоїть Архітектура, а по інший – Музика, яка також не може існувати без ритму, без рахунку, без яких в свою чергу немає гармонії.
Парфенон має 8 колонн вздовж коротких сторін і 17 по довгим. Виступи зроблені цілком з квадрату мрамору. Відношення висоти споруди до його довжини дорівнює 0,618. Якщо поділити Парфенон у пропорції «золотого поділу» то отримаємо певні виступи фасаду (додаток 8).
Скульптури мають увіковічнити знаменні події, зберегти в пам'яті імена славетних героїв та їх діяння. З давніх давен основу скульптури складала теорія пропорцій. Відношення частин людського тіла підпорядковувались пропорції “золотого перетину”, що виглядало гармонійно та красиво. Талія людини поділяє людське тіло в пропорції “золотого перетину”. Маємо як приклад статую Аполлона Бельведерского та статую Зевса Олимпийского (яка вважалась одним із чудес світу) та Афіни Парфенос.
2.5 Дроби і література
Ще з часів Піфагорійців, видатні математики захопились поезією і навіть намагалися писати самостійно. Ж. Дьедонне казав: “Прагнення математиків всіх часів: допитливість і потяг до краси ”. Велике математичне дарування зазвичай поєднується з проявом творчої цікавості до поезії. Математик Софія Василівна Ковалевська каже про математику так «Це наука, яка потребує дуже багато фантазії. Не можна бути математиком, в той же час не будучи поетом в серці».
Основою поезії являється рима. Рима – це переносна симетрія віршових кінцівок. Потреба симетрії кінцівок приводить до наступних необхідних умов рими: 1) римовані слова повинні мати однакову кількість складів після наголошеної голосної; 2) наголошені голосні повинні звучати однаково; 3) звуки після наголошеної голосної повинні бути схожими.
Бачимо, що дроби достатньо тісно пов'язані з мистецтвом. Мистецтво треба приймати і серцем і душею. Служити йому. Але якщо ми спробуємо прикласти математику до будь якої галузі мистецтва, то точно матимемо успіх.
Висновки
Дроби мають давню історію. При поділі здобичи, при вимірюванні величин, площ, спадку, тощо, люди почали використовувати поняття половини, третини, два з половиною кроки... Отже можна сказати, що дробові числа виникли як результат вимірювання величин. З'явились дроби.
Давні єгиптяни вже знали, як поділити 2 предмета на трьох. Для числа 2/3 та 3/4 вони мали спеціальний значок. Це був єдиний у їхньому вжитку дріб, в чисельнику якого не стояла одиниця. Якщо ж єгиптянину потрібно було використати інші дроби, то він подавав їх у вигляді суми основних дробів, тобто дробів, у яких в чисельнику була тільки 1, а в знаменнику будь яке інше число.
У стародавньому Вавилоні, навпаки. віддавали перевагу постійному знаменнику. В знаменнику було число 60.
Греки взагалі не вважали дроби числами, хоча і виконували всі операції над дробами. Дорогу в світ математики Греції дробам проклала музика.
Римляни теж вживали знаменник рівний 12. Величина 1/12 асса називалася унцією. Для дробів, знаменник яких отримували шляхом ділення частки на більш дрібні, були особливі назви.
Дії з дробами у середньовіччі вважались найскладнішою галуззю математики перш за все тому, що не було визначено чітких правил дій з дробами, зручного способу запису. Створювались таблиці що до дій з дробами. Народи пройшли через різні записи дробів, поки не дійшли до сучасного. Спочатку у записі дробів не використовувалась дробна риска. Сучасну систему запису дробів створили в Індії. Тільки там писали знаменник зверху, а чисельник знизу і дробну риску теж не писали. А записувати дроби в такому вигляді як зараз почали араби.
Дроби відіграють важливу роль і в мистецтві. Крім звичайних дробів та дробів у звичному розумінні в мистецтві широко використовують відношення “золотого перетину”, що також є застосуванням дробів. Для розстановки акцентів та побудови гармонії використовують різноманітні прийоми в основу яких покладено відношення 5/6. Тобто принцип “золотого перетину”
Робота над проєктом значно збагатила мій досвід. Крім отриманих додаткових загальних знань, я набула досвід в опрацюванні великої кількості матеріалу. А саме пошуку матеріалів, групуванні, систематизації та викладені.
Результати роботи можна використати для популяризації математичних знань.
Використані джерела
1. Дроби в нашому житті (інтернет ресурс)
http://drobvz.blogspot.com/p/blog-page_14.html
2. Звичайні дроби (інтернет ресурс)
https://sites.google.com/site/podorozkranoumatematiki/zvicajni-drobi
3. Історія виникнення дробів (інтернет ресурс) https://ua.waykun.com/articles/istorija-viniknennja-drobiv-socialna-merezha.php
4. Історія виникнення дробів (інтернет ресурс) http://mfedorova.blogspot.com/2014/06/blog-post.html
Додаток 1
Запис дробів в стародавньому Єгипті
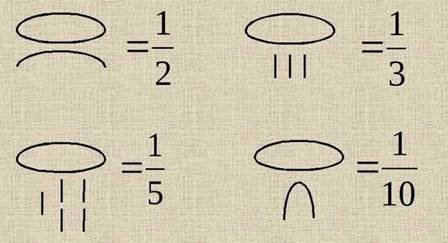
Додаток 2
Математичний папірус Рінда (початок 2 тисячоліття до нашої ери)
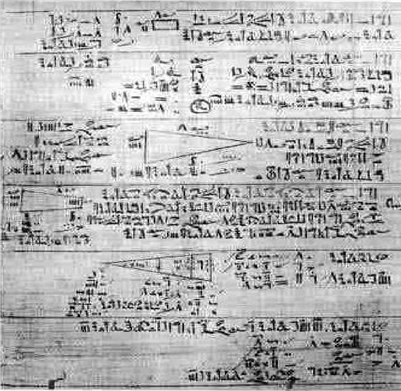
Додаток 3
Фрагменти табличок з стародавнього Вавилону


Додаток 4
Золоті трикутники в портреті

Додаток 5
Застосування поділу полотна в пропорції “золотого перерізу”

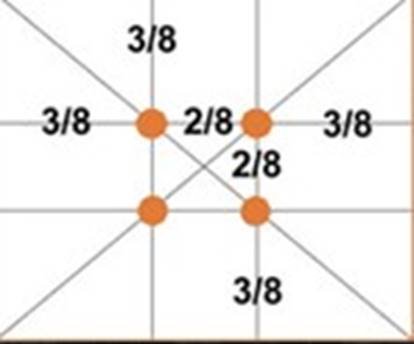
Додаток 6
Правило діагонального золотого перерізу

Додаток 7
Правило третин

Додаток 8
Парфенон

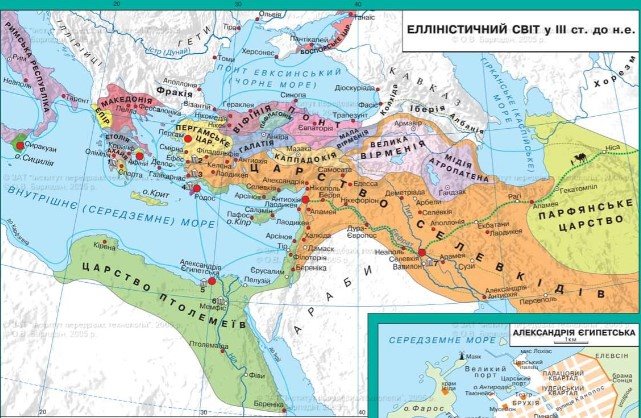
Додаток 9
Стародавні держави на карті


про публікацію авторської розробки
Додати розробку
