Урок - дослідження на тему: "Визначений інтеграл. Його фізичний і геометричний зміст"

Про матеріал

Дидактичний матеріал до нестандартного уроку - дослідження на тему: "Визначений інтеграл. Його фізичний і геометричний зміст", та опорний конспект на тему: "Визначений інтеграл та його застосування".

Перегляд файлу

Мета:

Навчальна: формування в учнів вміння застосовувати інтеграл до знаходження площ плоских фігур.

Розвиваюча: розвивати логічне мислення, пам'ять, увагу, математичну грамотність.

Виховна: виховувати акуратність, наполегливість, інтерес до вивчення математики.

Тип уроку: урок закріплення і удосконалення нових знань, умінь і навичок.

Вид уроку: урок - дослідження.

Конструктор уроку:

І. Організаційна частина.

ІІ. Перевірка домашнього завдання.

• Бліцопитування «Математичний розсип».

ІІІ. Актуалізація знань, умінь і навичок.

• Інтерактивна гра «Калейдоскоп формул».

IV. Повідомлення теми, мети і плану уроку. Мотивація навчальної діяльності учнів.

• Проблемна ситуація.

V. Сприйняття та усвідомлення нового матеріалу.

• Стратегія творчого пошуку: «Вилікуй» первісні та інтеграли;  опорний конспект.

VІ. Перевірка знань учнями фактичного матеріалу.

• Стратегія творчого пошуку «Віхор задач»

VІІ. Підведення підсумків.

• Стратегічний творчий пошук.

VІІІ. Рефлексія.

• Стратегічний творчий пошук «Принцип доповнюваності».

IX. Домашнє завдання. (диференційоване)

 Обов’язковий мінімум;  тренувальні завдання;  творчі завдання.

«Математичний розсип»

(перевірка домашнього завдання)

Початковий рівень

«Калейдоскоп формул»

(актуалізація) Середній рівень

(за кожну правильну відповідь – 1 бал) Співвіднести правильно формули.

*Функція*	*Первісна*
*хⁿ, n ≠ -1*	*lnx+C*
*1/x, >0*	*-cosx+C*
*e^x*	*xⁿ⁺¹/(n+1)*
*sinx*	*sinx+C*
*cosx*	*e^x*
*(кх+b)ⁿ,n ≠ -l‚ к ≠ 0*	*(sin(kx+b)/k)+C*
*1/(кх+ b), к ≠ 0*	*((кх+ b)ⁿ⁺¹/к(n+1)) +С*
*e^kx+b‚ k ≠ 0*	*(-cos(kx+b)/k)+C*
*sin(kx+b), k ≠ 0*	*(e^kx+b/k)+C*
*сos(kx+b), k ≠ 0*	*(ln(kx+b)/k)+C*

Проблемна ситуація

(мотивація)

Знайти площі заштрихованих фігур у кожному з випадків.

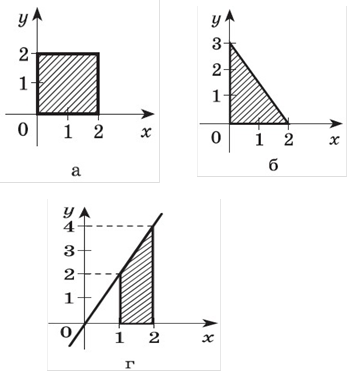
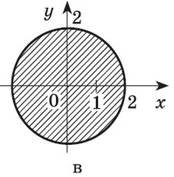
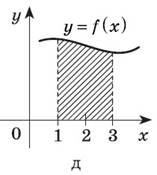
«Вилікуй» первісні та інтеграли

(осмислення нового матеріалу) Середній рівень

(за кожну правильну відповідь – 1 бал)

1. 2 ²2dxx33 2 83133 .  x

_1 _1

2. ^x ^x^dx xx^0,5 1⁴ 4 41 1624 _.

1 

x x ^0,5^0,50,5 _².

3. f x x ^x0_,5 x , Fxx 

«Віхор» задач

(закріплення нового матеріалу) Середній рівень

(за кожну правильну відповідь – 1 бал)

Для функції f(x) знайти первісну график якої проходить через точку М. а) f(x) = 4х-1, М(-1;3);

б) f(x) = sin2x, М(Π/2;5).

Достатній рівень

(за кожну правильну відповідь – 1 бал)

Обчисліть інтеграли:

а) ∫dx; б) ∫(3-2x)dx; в) ∫(3х²-4х+5) dx;

г) ∫(2х-3/√x)dx; д) ∫(sin(x/2)cos(x/2))dx;

е) ∫((4/х²)(1-2/х))dx; ж) ∫(4/(3х+2))dx

Рефлексія «Принцип доповнюваності»

Домашнє завдання (диференційоване)

«Опорний конспект» на тему:

«Визначений інтеграл та його застосування»

1. Обчислення визначеного інтеграла (Формула Ньютона - Лейбніца)

Формула

Приклад

Якщо функція f (x) визначена і не- перервна на відрізку [a; b], а F (x)— довільна її первісна на цьому відрізку

(тобто FR (x) = f (x)), то

Оскільки для функції f x x² однією

з первісних є Fx ^x³, то 3

²_2dxx3³1²23³13³73213. x

b^bFbFa

 f xdxFx^_a a

2. Криволінійна трапеція

Означення

Ілюстрація

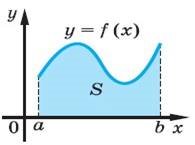
Нехай на відрізку [a; b] осі Ox зада- но неперервну функцію f (x), яка набуває на цьому відрізку тільки невід’ємних значень. Фігуру, обме_ жену графіком функції y = f (x), відрізком [a; b] осі Ox і прямими x = a і x = b, називають криволі_ нійною трапецією.

3. Площа криволінійної трапеції

Формула

Приклад

_f xdx a

Обчисліть площу фігури, обмеженої лініями y = sin x, y = 0, x_^,x_^

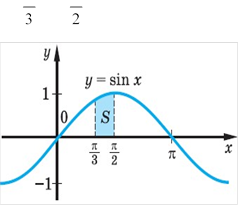
Розв’язання Зображуючи ці лінії,бачимо, що задана

фігура — криволінійна трапеція.



2 2 _

S   sin xdx  cos x

 3

«Опорний конспект» на тему:

«Визначений інтеграл та його застосування»

4. Властивості визначних інтегралів

_f xdx0 a

b _a

_f xdx_f xdx

a b

b _bb

_f xgxdx _f xdx_gxdx

a a a

b _b

_k f xdxk _f xdx

a a

Якщо функція f (x) інтегрована на [a; b] і c

[a; b], то

b _cb

_f xdx _f xdx_f xdx

a a c

5. Означення визначеного інтеграла через інтегральні суми

Нехай функція f (x) — неперервна на відрізку [a; b]. Виконаємо такі операції.

1. Розіб’ємо відрізок [a; b] на n відрізків точками x1, x2, ..., xn – 1 (вважаємо, що a = x0, b = xn).

2. Позначимо довжину першого відрізка через Δx1, другого — через Δx2 і т. д. (тобто Δx1= x1 – x0,

Δx2= x2 – x1, ..., Δxn= xn – xn– 1).

3. На кожному з одержаних відрізків виберемо довільну точку ci

(тобто ci [xi – 1; xi] , де i = 1, 2, ..., n).

4. Складемо суму Sn = f (c1) Δx1+ f (c2) Δx2+ ... + f (cn) Δxn. Цю суму називають інтегральною сумою функції f (x) на відрізку

[a; b].

_f xdx a

Якщо n →∞ і довжини відрізків розбиття прямують до нуля, то інтег- ральна сума Sn прямує до деякого числа, яке і називають визначеним інтегралом функції f (x) на відрізку [a; b] і позначають .

pdf

Завантажити

Зберегти на потім

Додав(-ла)

Криворотова Наталя Петрівна

Пов’язані теми

Алгебра, 11 клас, Матеріали до уроків

Додано

17 лютого 2019

Переглядів

3293

Оцінка розробки

Відгуки відсутні