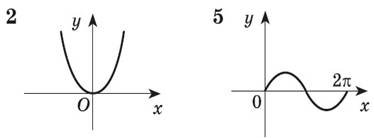Урок - семінар на тему: "Застосування інтеграла до обчислення площ плоских фігур"

Про матеріал

Дидактичний матеріал до нестандартного уроку - семінару на тему "Застосування інтеграла до обчислення площ плоских фігур".

Перегляд файлу

Мета:

Навчальна: формування в учнів вміння застосовувати інтеграл до знаходження площ плоских фігур.

Розвиваюча: розвивати логічне мислення, пам'ять, увагу, математичну грамотність.

Виховна: виховувати акуратність, наполегливість, інтерес до вивчення математики.

Тип уроку: урок закріплення і удосконалення нових знань, умінь і навичок.

Вид уроку: урок - семінар.

Конструктор уроку:

І. Організаційна частина.

ІІ. Перевірка домашнього завдання.

• Іінтерактивна вправа «Хто швидше»;

• інтерактивн гра «Математичне лото»;  сигнальні картки;  картки – завдання.

ІІІ. Актуалізація знань, умінь і навичок.

• Інтерактивна вправа «Відповідність»;  самостійна робота.

IV. Повідомлення теми, мети і плану уроку. Мотивація навчальної діяльності учнів.

• «Інформаційна палітра запитань».

V. Сприйняття та усвідомлення нового матеріалу.

• Стратегія творчого пошуку «Перетворюючого мислення»;  опорний конспект.

VІ. Перевірка знань учнями фактичного матеріалу.

• Стратегія творчого пошуку «Примусове поєднання»  робота в групах.

VІІ. Підведення підсумків. Рефлексія.

• Бліцопитування;  три дієслова.

VІІІ. Домашнє завдання. (диференційоване)

• Обов’язковий мінімум;

• тренувальні завдання; творчі завдання; міні проект.

Інтерактивна вправа «Хто швидше»

(робота в групах, перевірка Д/з) Заповніть таблицю:

І рівень (1 бал)

Обчисліть інтеграл:

1 2 2

a) xdx; b⁾x²dx; c)cos xdx.

⁰ ⁰ ^

Відповідь:

ІІ рівень (2 бали)

Відомо, що Знайдіть :

b a

 f xdx 5  f xdx a b

Відповідь:

ІІІ рівень (3 бали)

Обчисліть :

5x1^dx.

Відповідь:

Інтерактивна гра «Математично лото »

Заповніть таблицю, поклавши

відповідні сигнальні картки зворотною стороною.

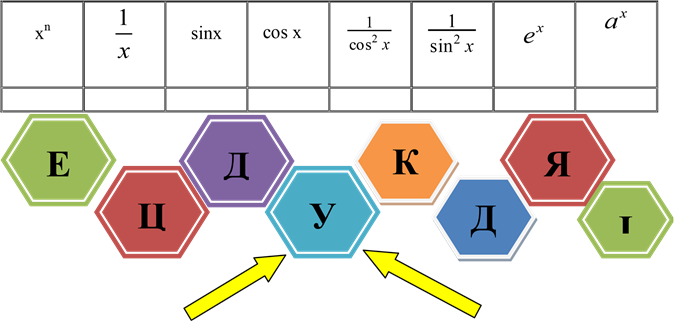
Метод міркувань від складного до простішого?

Інтерактивна вправа «Відповідність» (Самостійна робота, актуалізація) Середній рівень (3 бали)

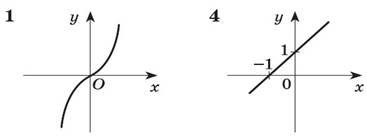
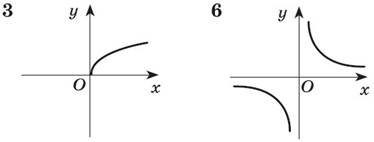
1. Установіть відповідність між графіком і функцією.

	А	1 у x
	Б	уx1
	В	1 у ₂ x
	Г	уx²
	Д	у х
	Е	уx3
	Ж	уsin x

Достатній рівень (3 бали)

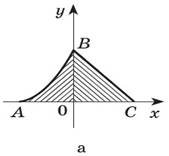
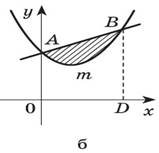
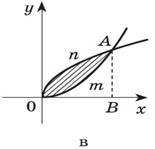
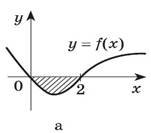
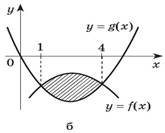
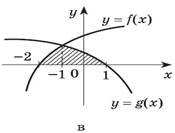
1. Запишіть у вигляді суми або різниці площ криволінійних трапецій площу заштрихованих фігур.

«Інформаційна палітра запитань»

(мотивація)

1. Що ми знаємо про інтеграл?

2. На практиці часто доводиться обчислювати площі фігур, які не є криволінійними трапеціями. Як це зробити застосовуючи вже отримані знання про площу криволінійної трапеції?

Творчий пошук «Перетворююче мислення» (сприйняття та усвідомлення нового матеріалу)

Колективне розв’язування

Приклад 1

Обчисліть площу фігури, обмеженої лініями y ^x, та yx².

Розв’язання

Коментар

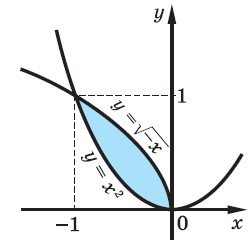
1. Зобразимо задані лінії (рис.) і знайдемо абсциси точок їх перетину:

2. ^x² х , (1)

3. Тоді х4 = –х, х4 + х = 0,

4. х (х3 + 1) = 0,

5. х = 0 або х = – 1 (обидва корені задовольняють рівнянню (1)).

6. Площа заданої фігури дорівнює

0 00

S  _ xx²dx xdxx²dx

1 1 1

2 3 0 x3 0 1  x2   3 1 3 1 3 .

1. Зображуючи задані лінії (рис.), бачимо, що шукана фігура знаходиться між графіками двох функцій.

2. Зверху вона обмежена графіком функції f₂x  х , а знизу — графіком функції f₁x x².

3. Отже, її площу можна обчислити за формулою

S^ ^f₂x ^f₁x^dx.

a

4. Щоб знайти межі інтегрування, знайдемо абсциси точок перетину графіків заданих функцій.

5. Оскільки ординати обох кривих у точках перетину однакові, то достатньо розв’язати рівняння f1

(x) = f2 (x).

6. Для розв’язування одержаного ірраціонального рівняння можна ви- користати рівняння-наслідки (у кін- ці виконати перевірку) або рівно- сильні перетворення (на ОДЗ, тобто при x ≤ 0).

7. Відзначимо також, що на одержа- ному відрізку [–1; 0] значення (– x) ≥ 0. Тоді x x .