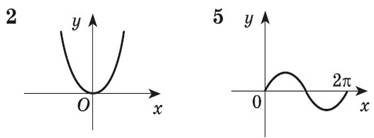Урок - гра на тему: "Розв`язування вправ"
 |
Мета:
Навчальна: формування вміння в учнів застосовувати інтеграл до обчислення площ плоских фігур.
Розвиваюча: розвивати логічне мислення, пам'ять, увагу, математичну грамотність.
Виховна: виховувати акуратність, наполегливість, інтерес до вивчення математики.
Тип уроку: застосування знань, умінь і навичок.
Вид уроку: урок - гра.
Конструктор уроку:
І. Організаційна частина.
ІІ. Перевірка домашнього завдання.
• Міні проект;
• інтерактивна гра «Інформаційна палітра»
ІІІ. Актуалізація знань, умінь і навичок.
• Інтерактивна гра «Унікум»
IV. Повідомлення теми, мети і плану уроку. Мотивація навчальної діяльності учнів.
• План уроку (правила гри).
V. Удосконалення вмінь і навичок.
• Інтерактивна вправа «Альпініст»; опорний конспект.
VІ. Застосування знань, умінь і навичок.
• Самостійна робота
VІІ. Підведення підсумків.
• Рефлексія («Зв'язок поколінь»)
VІІІ. Домашнє завдання.
• Обов’язковий мінімум; тренувальні завдання; творчі завдання.
План уроку (правила гри):
1. Учні – детективи – початківці хочуть отримати роботу.
2. Для цього треба скласти резюме.
3. Пройти стажування.
4. Обговорити заробітну платню.
1. Резюме для роботодавця
Інтерактивна гра «Інформаційна палітра»
(перевірка Д/з)
Початковий рівень (за кожну правильну відповідь – 0,5 балів)
|
Я можу Я вмію Я знаю Я вивчив Я сьогодні Я завжди |
1. 2. Правила обчислення первісних 3. Формулу Ньютона - Лейбніца 4. Означення криволінійної трапеції 5. Формулу знаходження площі криволінійної трапеції 6. Формулу, за якою можна знайти абсцису вершини параболи 7. Алгоритм знаходження площ плоских фігур 8. ……….( свій варіант) |
2. Стажування
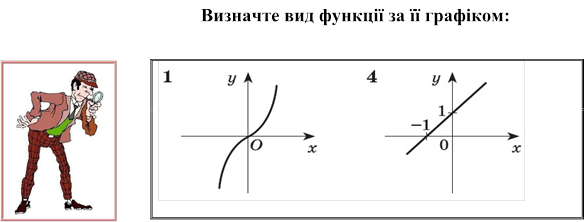
Інтерактивна гра «Унікум»
(актуалізація)
Середній рівень (за кожну правильну відповідь – 1 бал)
|
|
|
3. Стажування (робота в парах)
Інтерактивна вправа «Альпініст»
(удосконалення вмінь і навичок)
Середній рівень (за кожну правильну відповідь – 1,5 бали)
Пара, яка першою виконає завдання , записує відповідь на дошці.
|
Знайдіть площу фігури, обмеженої лініями: |
|
1 yx2 2x2 і y 24xx2 |
|
7 2
y x |
4. 
 Обговорення
заробітної платні
Обговорення
заробітної платні
(Самостійна робота)
«Прес - конференція» (осмислення нового матеріалу) Початковий рівень (3 бали)
|
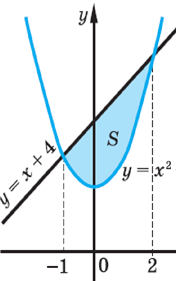
Укажіть вираз для знаходження площі заштрихованої фігури, зображеної на малюнку. |
||
|
1 А. x2dx 1 |
1 В. x2dx 0 |
|
|
1 Б. x2dx 1 |
1 Г. x2dx 1 |
|
Середній рівень (3 бали)
|
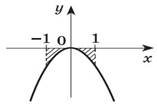
Укажіть формулу для обчислення площі фігури, зображеної на малюнку. |
||
|
2 А. (2xx2)dx 1 |
2 В. (2xx2)dx 1 |
|
|
2 Б. (x2 x2)dx 1 |
2 Г. (x2x2)dx 1 |
|
Достатній рівень (3 бали)
|
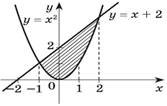
Обчисліть площу фігури,обмеженої лініями: |
|
yx2 4x4і yx4 |
Високий рівень (3 бали)
|
Обчисліть площу фігури,обмеженої лініями: |
|
y
sin
xі ycosx,
0x |
5. «Зв'язок поколінь»
(рефлексія)
|
1. Ким із детективів ви сьогодні себе відчували? Чому? |
|
|
2. Що сподобалося або не сподобалося на уроці? Оцініть свою роботу сьогодні. |
Домашнє завдання (диференційоване)

Індивідуально. Обчислити площу фігури, обмеженої лініями: у2x у 923x
«Опорний конспект» на тему:
«Обчислення площ за допомогою визначених інтегралів»
|
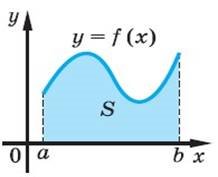
1. Площа криволінійної трапеціії |
||||
|
Означення |
Ілюстрація |
|||
|
Площа криволінійної трапеції, обмеженої графіком неперервної невід’ємної на відрізку [a; b] функції f (x), віссю Ох і прямими x = a і x = b, дорівнює |
|
|||
|
|
b S f xdx a |
|
||
|
2. Площа фігури, обмеженої графіками двох функцій і прямими x = a і x = b. |
||||
|
Формула |
Приклад |
|||
|
Якщо на заданому відрізку [a; b] неперервні функції у = f1 (x) і у = f2 (x) мають ту
властивість, що f2x
f1x
для всіх х
|
Обчисліть площу фігури, обмеженої лініями yx2 2, yx4 Розв’язання
2 S x 4x2 2dx 1 2 x 2 x2dx 1
|
|||


про публікацію авторської розробки
Додати розробку